trigonometrisk likhet

$$\begin{gathered} VL={(1-\frac{2\tan x}{\tan 2x})}^2={(1-\frac{2\tan x}{{\displaystyle \frac{2\tan x}{1-{\tan }^{2}x}}})}^2={\left(\tan 2x\right)}^2={\tan }^{4}x \\ HL={(1-\frac{2\tan x}{\sin 2x})}^2={(1-\frac{2\tan x}{\sin 2x})}^2={(1-\frac{1}{{\cos }^{2}x})}^2={(1-\frac{{\sin }^{2}x+{\cos }^{2}x}{{\cos }^{2}x})}^2= \\ ={(-{\tan }^{2}x)}^2={\tan }^{4}x \end{gathered}$$

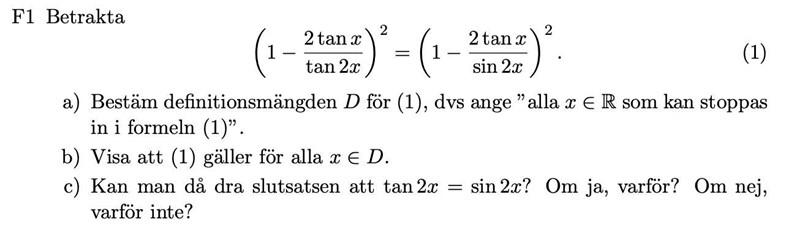
a)D för (1) är alla x utom $x\ne \frac{\mathrm{\pi }}{4}k, där k\in z$

b) Hur visar jag det förutom något tafatt som ''det är de enda värden där nämnaren är 0 och odefinierad''?

c)Nej, anledningen till att VL och HL är lika i uppgiften är pga att uttrycken inom paranteserna kvadreras och därmed är absolutbeloppen samma inom paranteserna, men det går inte att säga att tan2x=sin2x därför.

Synpunkter på mitt resonnemang?