Trigonometriska funktionsvärden
Hej misstänker att facit är fel, om någon har tid att bekräfta/falsifiera detta?
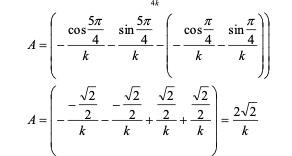
Facits räkneoperation som jag anser är fel?
Hur jag vill skriva
Facit är rätt.
Sista steget i din uträkning är inte rätt.
är inte lika med .
Repetera hur du går från dubbelbråk till enkelbråk. Ditt sista steg förstår jag inte alls.
Förläng istället med :
Också. Det som jag skrivit innanför parentesen är ju inte samma som facit, men när jag tittar på funktionsvärden stämmer mina siffror?
nyfikenpåattveta skrev:Också. Det som jag skrivit innanför parentesen är ju inte samma som facit, men när jag tittar på funktionsvärden stämmer mina siffror?
Prova nåt enklare: 2*2*2*2/2, är det 3*2?
nyfikenpåattveta skrev:Också. Det som jag skrivit innanför parentesen är ju inte samma som facit, men när jag tittar på funktionsvärden stämmer mina siffror?
Du blandar ihop multiplikation med addition.
Det du tänker på är .
Men det som står är
Såklart, vilken miss... Tack för ert tålamod och tid :)




