Trippel Integral

Hej, jag behöver hjälp med denna uppgift:

Låt K vara den del av klotet $x^{2} + y^{2} + z^{2} \leq 25$ som ligger ovanför ytan $z = - \sqrt{3} \sqrt{x^{2} + y^{2}}$ och som uppfyller villkoren $0 \leq y o c h \sqrt{3} y \leq x$ . Beräkna $\int \int \int_{K} y d V$ genom att införa sfäriska koordinater.

Jag känner till konverteringen till sfäriska koordinater så jag vet att y kan skrivas som rsin(u)sin(v). Dessutom vet jag att $0 \leq u \leq π$ , $0 \leq v \leq 2 π$ , och att $0 \leq r \leq 5$ .

Jag har också fått fram att Jacobi-determinanten för varaibelbytet är r²sin(u). Men sen är jag lite förvirrad för jag vet inte om jag måste göra något med de initiala villkoren eller om de inte spelar någon roll. Ska jag liksom bara köra trippel integralen med de sfäriska gränserna och den transformerande dV termed, med rsin(u)sin(v) som integrand? Sen vad betyder det ens att jag trippel integrerar y? Ger det mig en volym? Eller något annat? Så många frågor...

Tacksam för svar! :)

Hej,

Angående din sista fråga: Du kommer få enheten [y]*[V], där [V] är dimensionen för volym och [y] är enheten för y. Så beroende på vilken storhet vi definierar y till att vara kommer vi få en viss dimension på trippelintegralen.

Skulle vi vilja integrera över hela klotet är det bara att köra på med de gränser du tagit fram, samt jacobi-determinanten. Dock har vi 3 till begränsningar vi måste ta hänsyn till. Dessa kommer påverka integrationsgränserna. Det kluriga är att just ta reda på hur.

y>=0 är den lättaste, den kommer påverka en av vinklarna på ett tydligt sätt. Även sqrt(3)y<=x kommer ge en begränsning på samma vinkel. Den sista begränsning blir lättare att tyda om du ritar upp den i en 3D graf (SPOILER: den kommer påverka gränserna för den andra vinkeln).

Ok om vi tittar först på $r \sin (u) \sin (v) \geq 0$ , dvs $y \geq 0$

så ser vi att villkoret är sant då båda sinus-termerna är positiva. dom är ju det när vinkeln är mellan 0 och pi, så jag antar att det måste gälla för båda termerna? Men då betyder det att detta gäller för både u och v, vilket inte kan stämma med tanke på att vi har andra villkor som måste tas hänsyn till :/ Glömde till och med att lägga till att i uppgiften antas rummet R3 svara mot $r \in [0, \infty), u \in [0, π], v \in [- π, π]$

Eftersom att sin(u)>=0 för alla tillåtna u måste vi ha att sin(v)>=0, detta ger oss ett krav på v enbart, u kan vara fritt.

Hur tänker du med nästa begränsning?

Jag hade nog börjat med y=0 och funderat ut vilken vinkel konen har. Lutningen -sqrt(3) är närmast klassisk :)

Nedan visas en bild utan restriktionen x≥sqrt(3)y

Visa spoiler

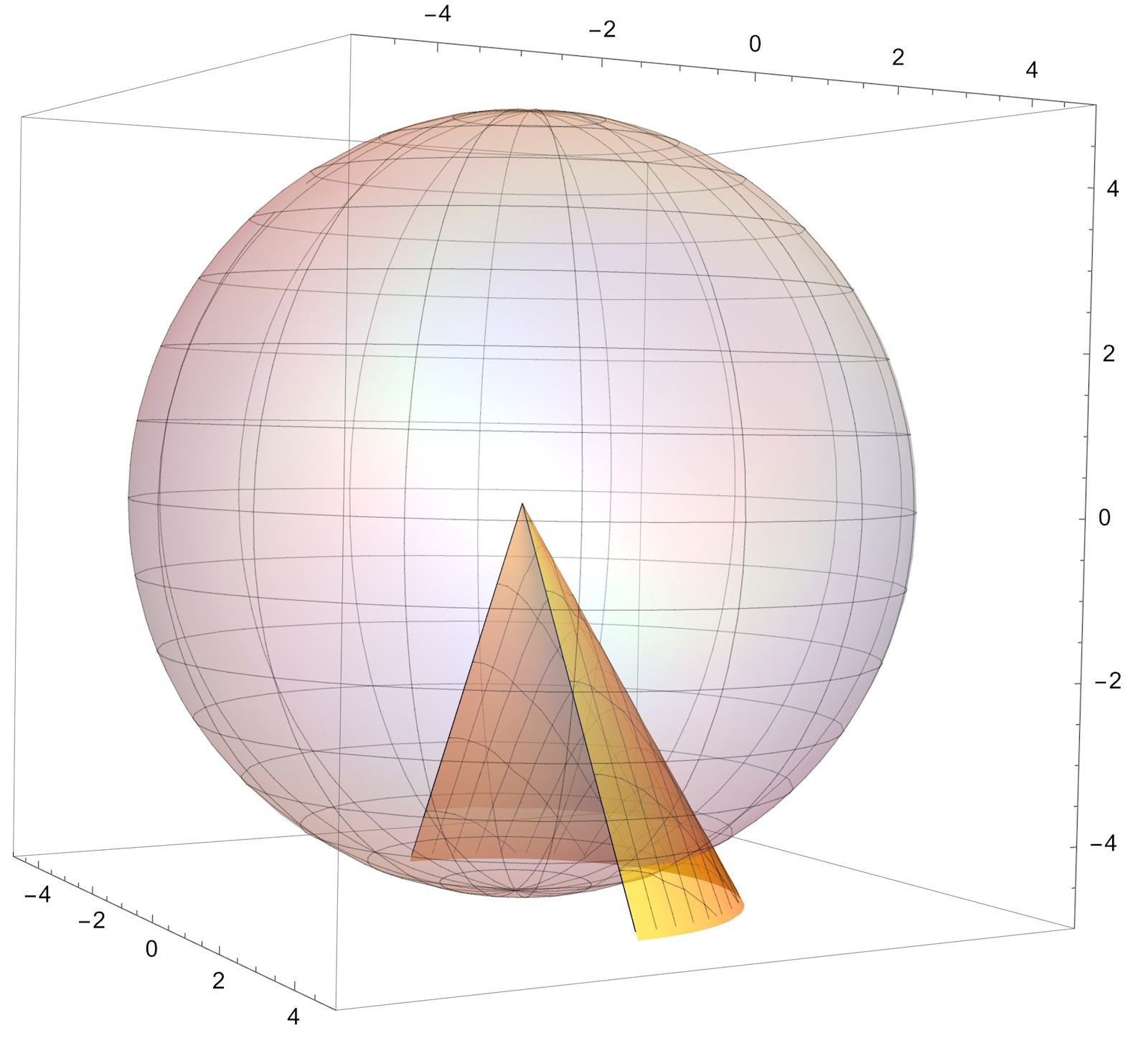
Ok så jag satte in de sfäriska koordinat uttrycken in för z, x, och y i ekvationen för konen och när jag löste den försvann termerna med v och jag fick fram att u = pi/6 (fick också -pi/6 men det ligger ju inte i intervallet för u) vilket jag antar borde vara vinkeln för konen. Sedan har jag villkoret $\sqrt{3} y \leq x \Rightarrow \sqrt{3} r \sin (u) \sin (v) \leq r \sin (u) \cos (v)$

jag tänkte sedan att jag kan hitta vilket intervall u måste integreras på från olikheten men jag fick ju u till ett bestämt värde så jag får bara att $\frac{\sqrt{3}}{2} r \sin v \leq \frac{r \cos v}{2}$ , vilket inte hjälper. Eller ska u bara integreras från 0 till pi/6??

Det är inte helt klart för mig vad av u och v som är longitud och latitud (vissa böcker har phi och theta och de brukar växla om), men dina värden är (nästan) rätt.

Konen är på vinkel -π/3 (-60°) och begränsningen i xy-planet är [0,π/6] alltså har vi vinkelintervallen

[-π/3,π/2] och [0,π/6] samt [0,5] för r.

(Om jag nu minns rätt om hur vinklarna är orienterade.... Calle kan säkert rätta mig om det skulle vara fel!)

vart kommer [-π/3,π/2] ifrån? Förresten är det u som ska vara phi och v som ska vara theta.

Sorry, jag yrade bort mig i diverse gamla beteckningar.

Du skall vi se

phi är kolatituden (mäts från nordpolen, phi = 0, till sydpolen phi = π)

theta är longituden (mäts som vanligt i xy-planet med theta=0 längs positiva x-axeln)

har vi att

0 ≤ phi ≤ π/2+π/3 = 5π/6

0 ≤ theta ≤ π/6

0 ≤ r ≤ 5.

Konen har en lutning på -60°, d.v.s. -π/3, alltså skall phi gå från nordpolen ned till konen vilket är π/2+π/3 = 5π/6

I xy-planet har vi att sqrt(3)y≤x dv.s. y≤y/sqrt(3) vilket är sektor med öppningsvinkel π/6. Alltså har vi 0 ≤ theta ≤ π/6

Integralen kan nu skrivas

INT_{r=0}^5 INT_{phi=0}^{5π/6} INT_{theta=0}^{π/6} r sin(phi)sin(theta) * r^2 sin(phi) dphi dtheta dr.

Denna är "separabel" och blir

INT_0^5 r^3 dr * INT_0^{5π/6} sin^2(phi) dphi * INT_0^{π/6} sin(theta) dtheta

= 625/4 * (sqrt3/8 + 5π/12) * (1 - sqrt3/2)

= 625/192 (2 - sqrt3) (3 sqrt3 + 10π) ≈ 31.9342

Inget vidare snyggt svar…

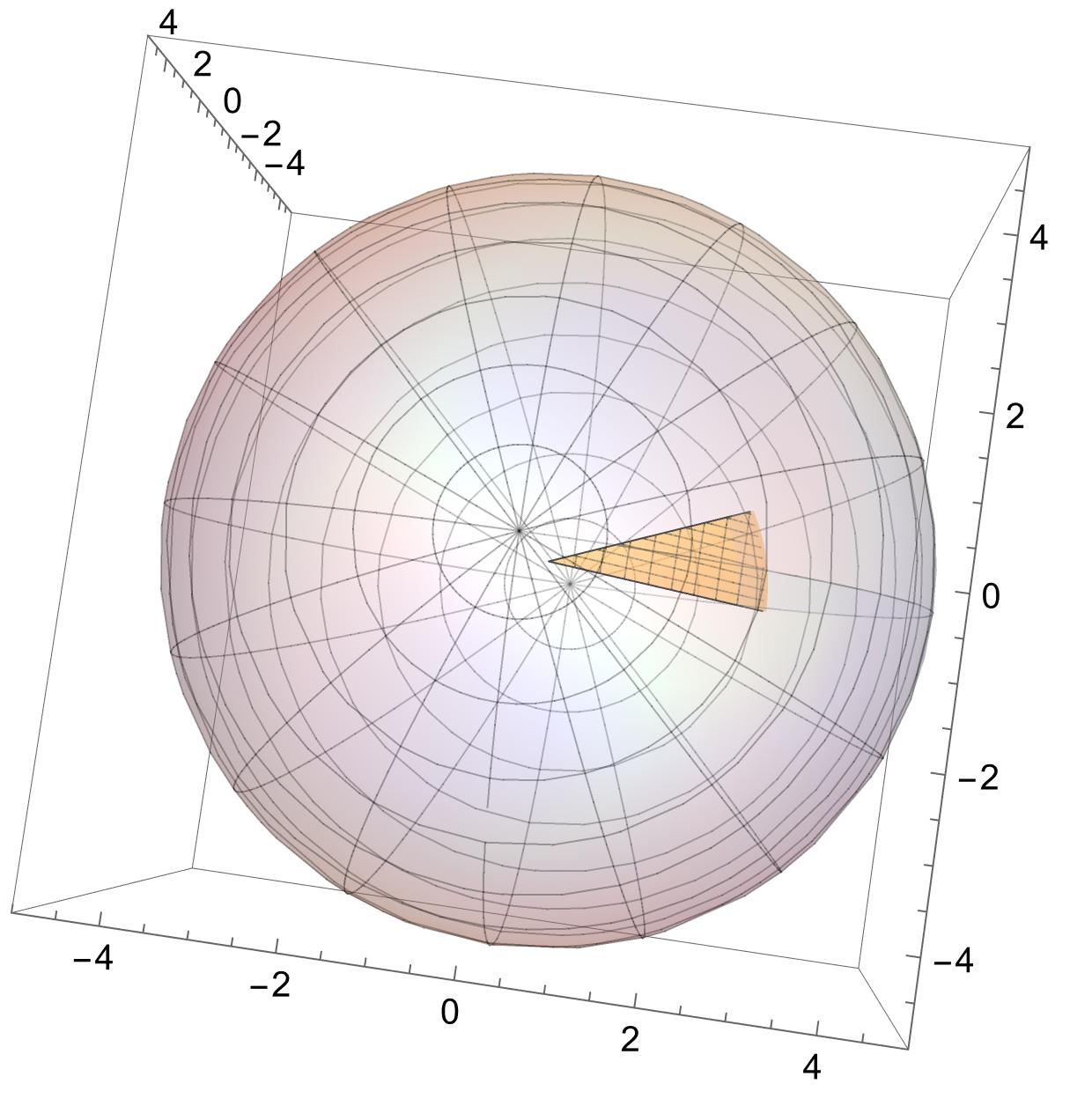
Här en enkel bild på begränsningen ovanifrån

Tack för hjälpen! Ska kolla över allt igen imorgon och se om jag förstår, återkommer om jag har frågor!

Arminhashmati skrev:
Tack för hjälpen! Ska kolla över allt igen imorgon och se om jag förstår, återkommer om jag har frågor!

Lite snyggare skrivet;

Svara

Visa senaste svar