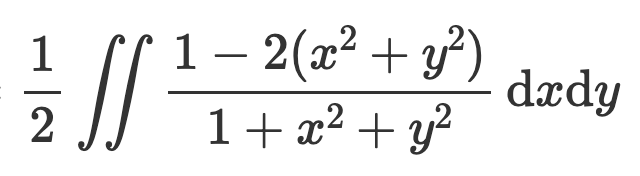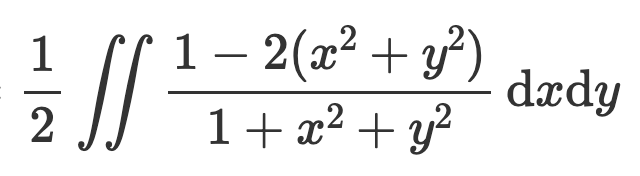Trippelintegral
Hej!
Jag vet att området är ett klot men jag vet inte hur jat ska tänka med z>=sqrt(x^2+y^2).

är ju radien, i cylinderkoordinater. Som om du tänker på saken är
Implicit betyder det ju också att
D4NIEL skrev:är ju radien, i cylinderkoordinater. Som om du tänker på saken är
Implicit betyder det ju också att
Var kommer rho ifrån? Om det är som att säga att z>0 så kan jag förstå. I facit fick de (3ln(3/2)-1)*pi/2 medan jag fått (ln(2)-1)*pi/2
Såhär ser min röriga lösning ut.

Hänger ej med i dina räkningar. Jag tror du förenklar det. Visa varje steg så kanske vi kan se var de går fel.
Trinity2 skrev:Hänger ej med i dina räkningar. Jag tror du förenklar det. Visa varje steg så kanske vi kan se var de går fel.
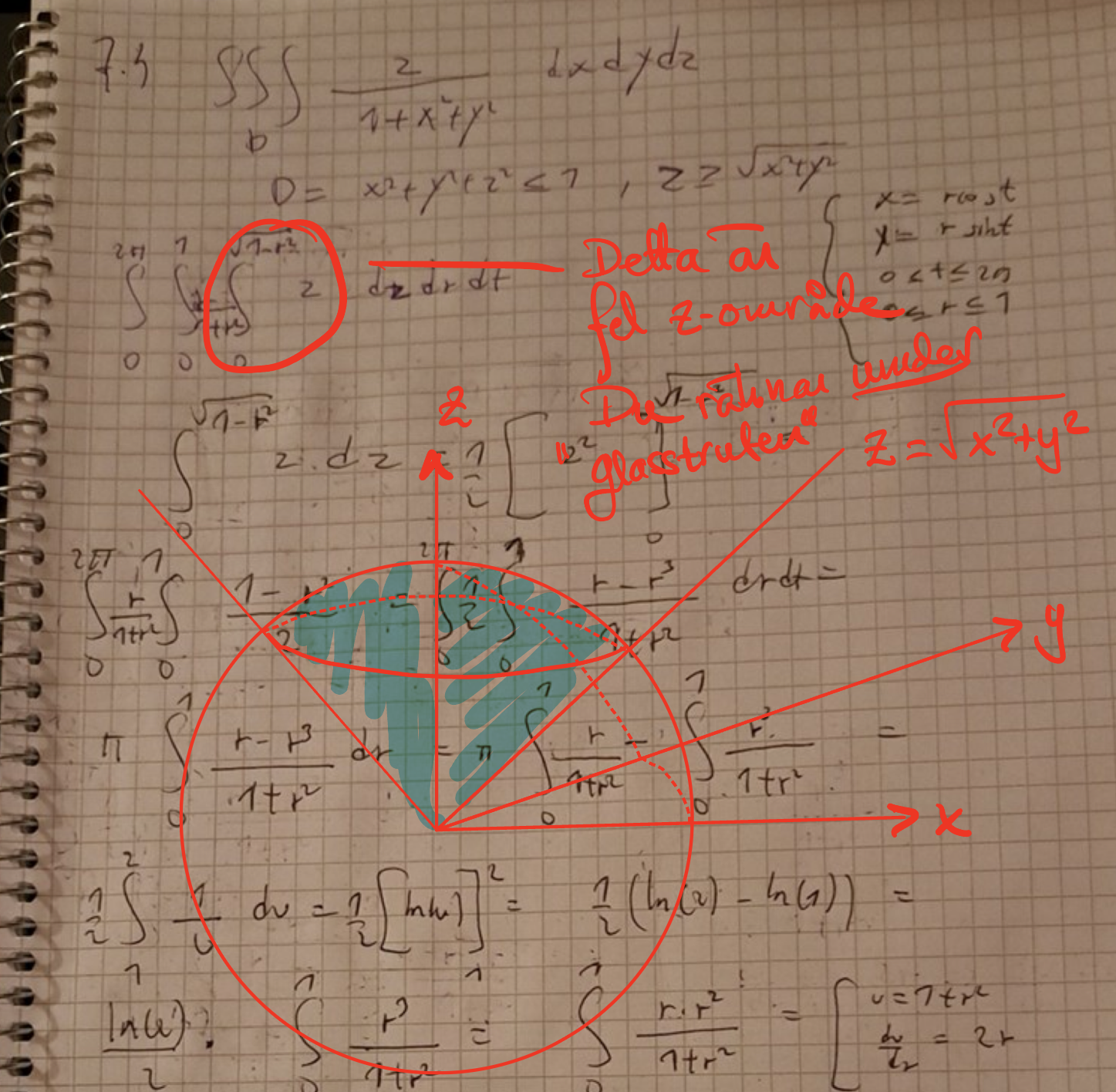
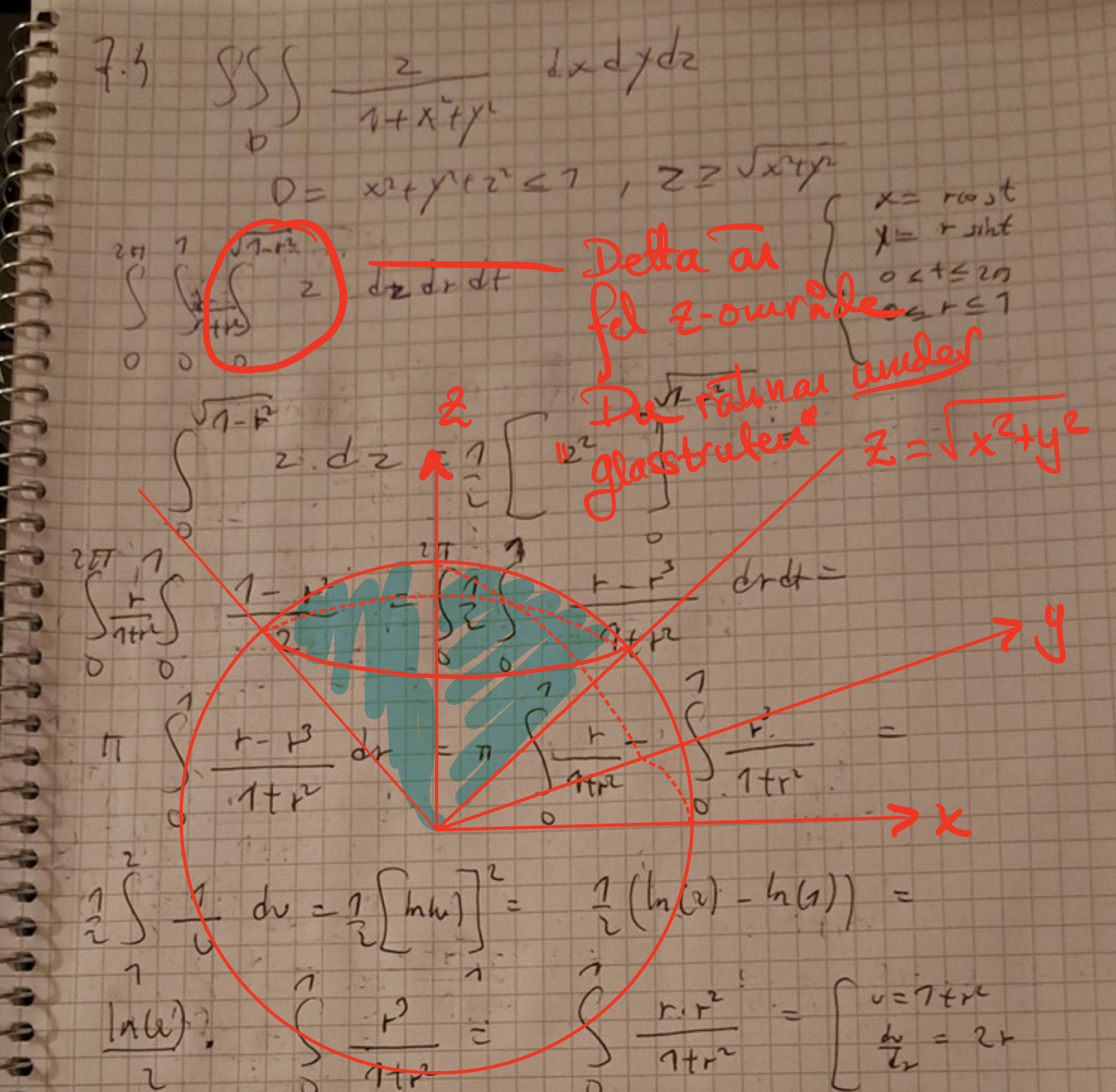
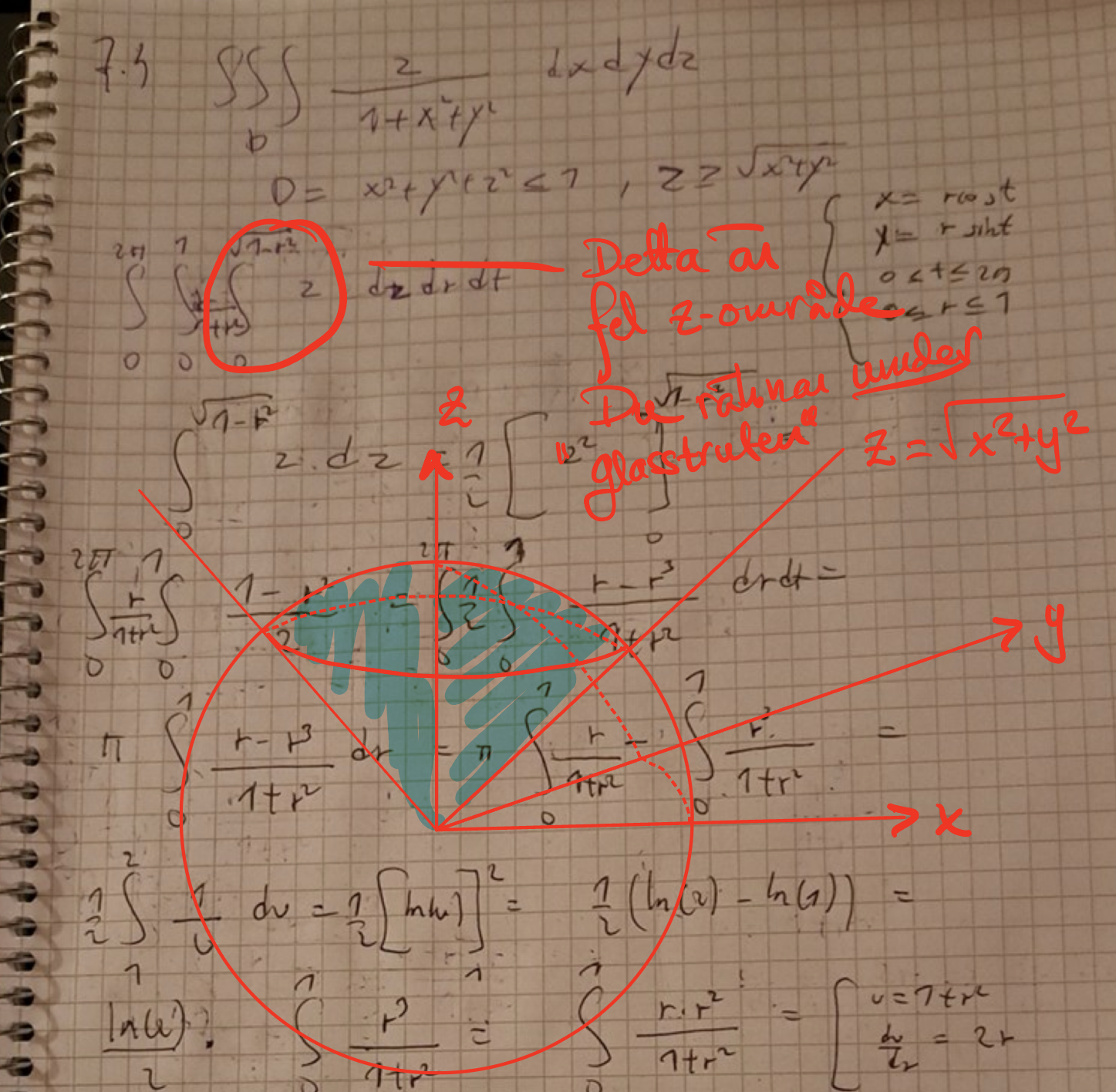
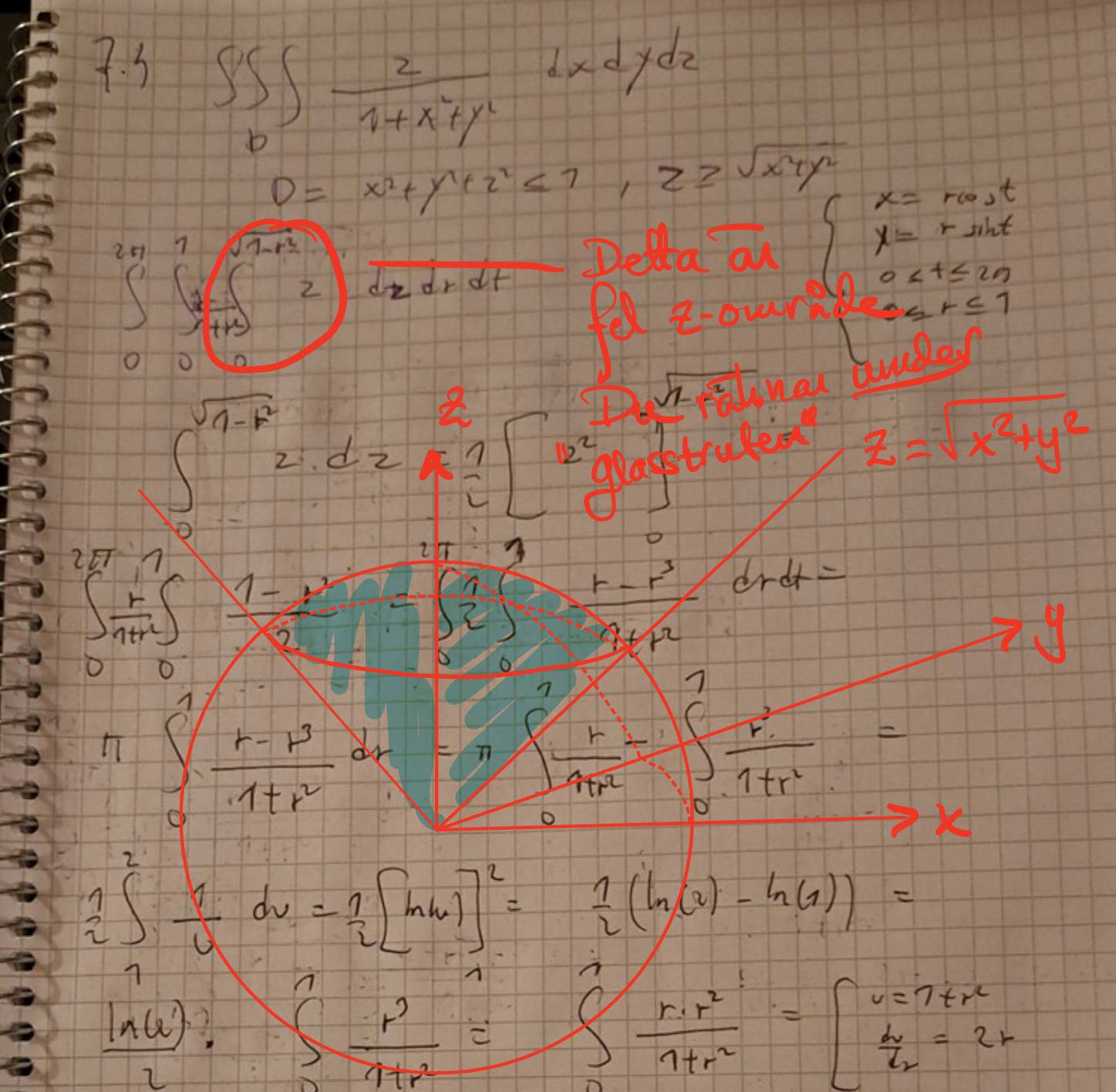
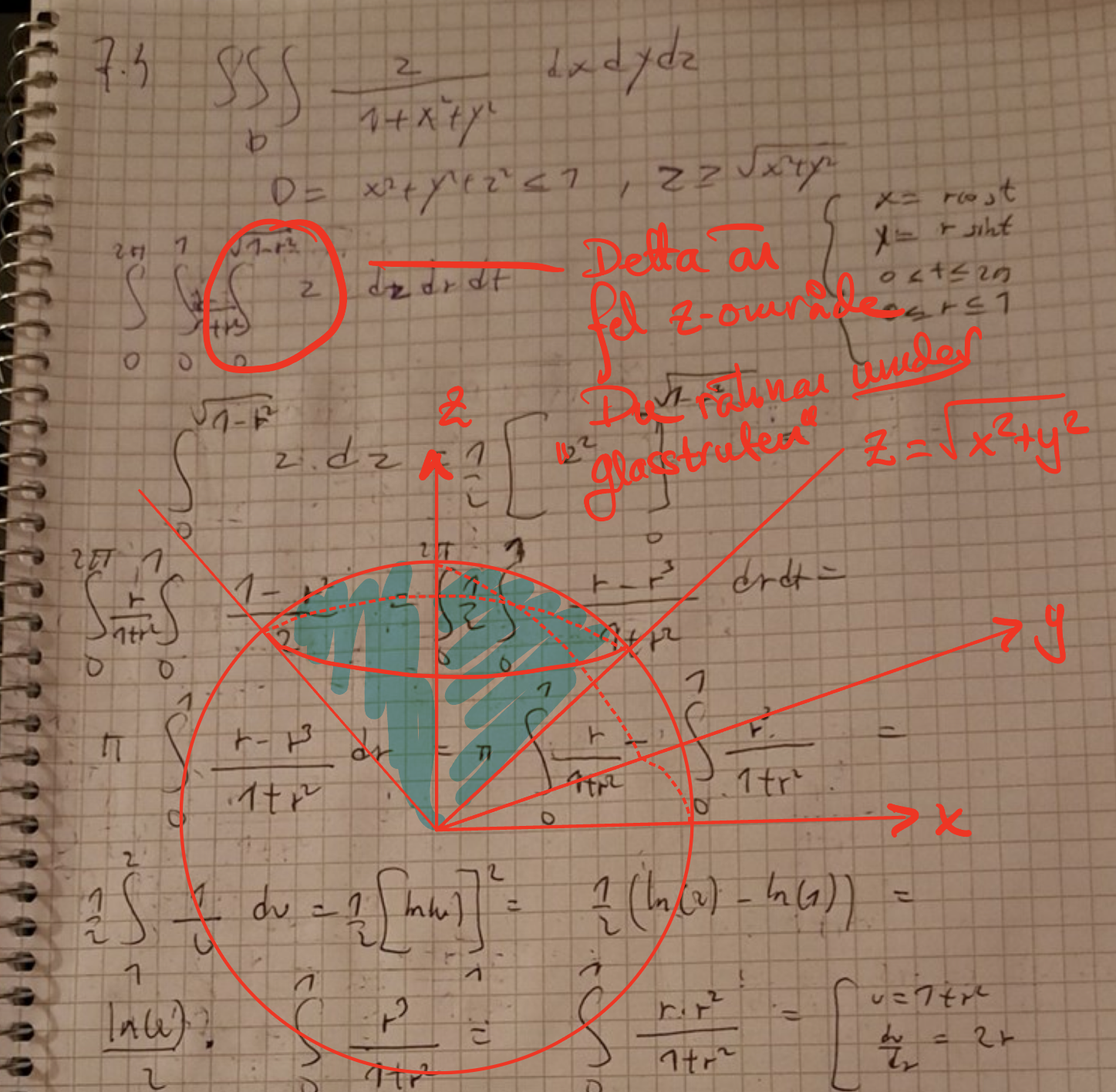
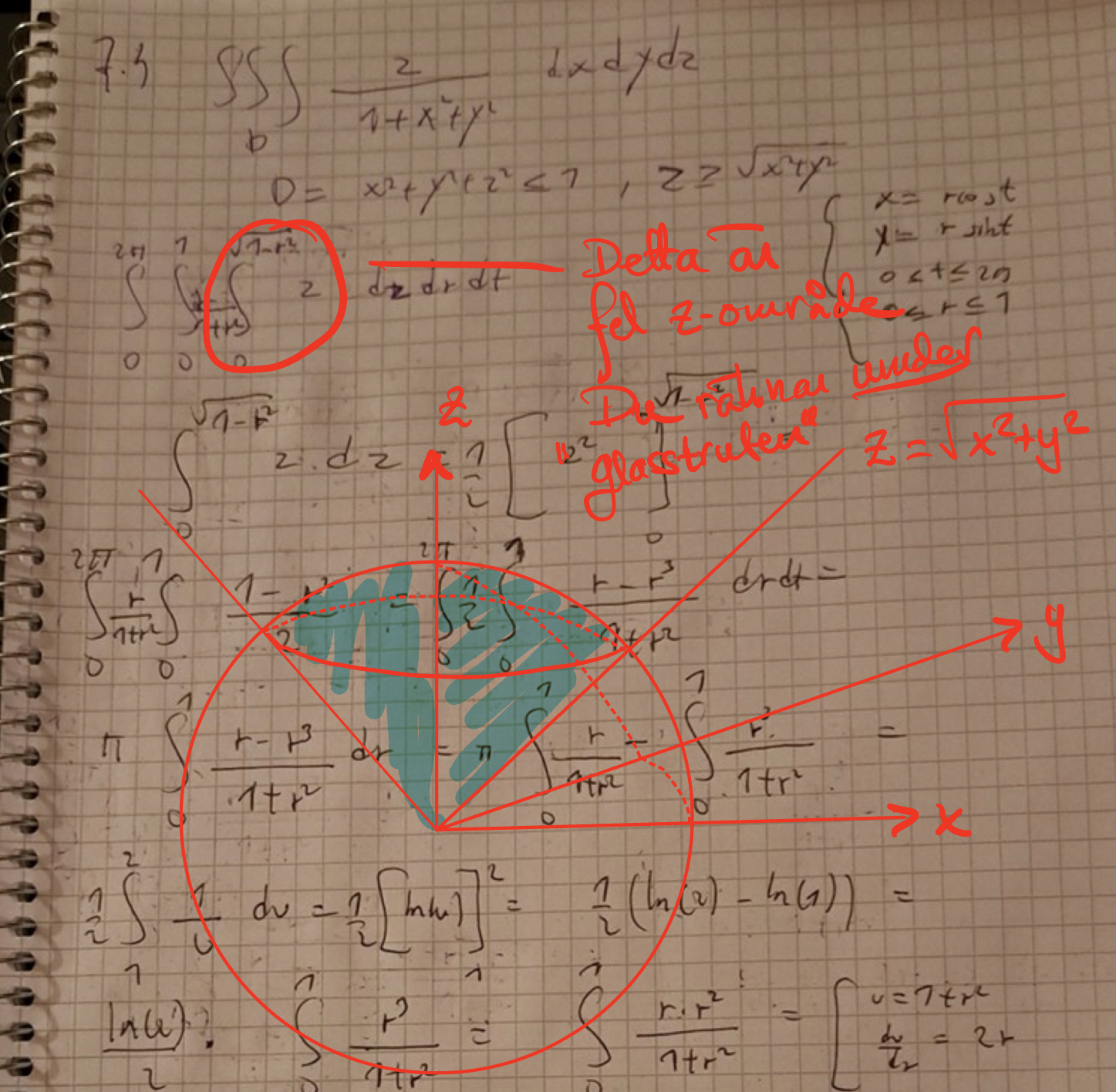
Okej nu har jag ny lösning men det blir fortfarande inte samma svar som facit. Se bild här. Jag inför polära koordinater samt använder z=sqrt(1-r^2) och z=0 för att integrera map på z. Se bild nedan. Slutgiltiga svar jag får är då pi/2*(2ln(2)-1). Facits svar däremot är andra bilden.


Trinity2 skrev:
Under glasstruten har vi x^2+y^2+z^2<=1 menar du? Men isåfall har vi området x^2+y^2<=1 för xy planet och z går från 0 till sqrt(x^2+y^2)? Hur påverkas gränserna för vinkel t för polära koordinater byte? Är det fortfarande 0 till 2pi?
destiny99 skrev:Trinity2 skrev:
Under glasstruten har vi x^2+y^2+z^2<=1 menar du? Men isåfall har vi området x^2+y^2<=1 för xy planet och z går från 0 till sqrt(x^2+y^2)? Hur påverkas gränserna för vinkel t för polära koordinater byte? Är det fortfarande 0 till 2pi?
Jag tror det blir enklare om man går över till rympolära koordinater och anger de r, theta och phi som definierar glasstruten. Man kan räkna som du gör också, men då skall z gå från sqrt(x^2+y^2) till sqrt(1-(x^2+y^2)) och det gäller att tänka på övre begränsning för x^2+y^2. (Konen är 45°-kon så skärning med sfären sker ej då x^2+y^2=1.)
Här är en enkel och tydlig beskrivning på rymdpolärt koordinatbyte
https://courses.mai.liu.se/GU/TATA69/M/presentationer/teori11del2.pdf
Trinity2 skrev:destiny99 skrev:Trinity2 skrev:
Under glasstruten har vi x^2+y^2+z^2<=1 menar du? Men isåfall har vi området x^2+y^2<=1 för xy planet och z går från 0 till sqrt(x^2+y^2)? Hur påverkas gränserna för vinkel t för polära koordinater byte? Är det fortfarande 0 till 2pi?
Jag tror det blir enklare om man går över till rympolära koordinater och anger de r, theta och phi som definierar glasstruten. Man kan räkna som du gör också, men då skall z gå från sqrt(x^2+y^2) till sqrt(1-(x^2+y^2)) och det gäller att tänka på övre begränsning för x^2+y^2. (Konen är 45°-kon så skärning med sfären sker ej då x^2+y^2=1.)
Här är en enkel och tydlig beskrivning på rymdpolärt koordinatbyte
https://courses.mai.liu.se/GU/TATA69/M/presentationer/teori11del2.pdf
Ja precis! Jag får fortfarande inte rätt svar dock. Så med vilka gränser varierar r då om vinkeln går mellan 0 till pi/4

destiny99 skrev:Trinity2 skrev:destiny99 skrev:Trinity2 skrev:
Under glasstruten har vi x^2+y^2+z^2<=1 menar du? Men isåfall har vi området x^2+y^2<=1 för xy planet och z går från 0 till sqrt(x^2+y^2)? Hur påverkas gränserna för vinkel t för polära koordinater byte? Är det fortfarande 0 till 2pi?
Jag tror det blir enklare om man går över till rympolära koordinater och anger de r, theta och phi som definierar glasstruten. Man kan räkna som du gör också, men då skall z gå från sqrt(x^2+y^2) till sqrt(1-(x^2+y^2)) och det gäller att tänka på övre begränsning för x^2+y^2. (Konen är 45°-kon så skärning med sfären sker ej då x^2+y^2=1.)
Här är en enkel och tydlig beskrivning på rymdpolärt koordinatbyte
https://courses.mai.liu.se/GU/TATA69/M/presentationer/teori11del2.pdf
Ja precis! Jag får fortfarande inte rätt svar dock. Så med vilka gränser varierar r då om vinkeln går mellan 0 till pi/4
Jag tror du rör ihop begreppen en aning.
Antingen så arbetar du i xy-planet med 0≤x^2+y^2≤1/sqrt(2) och efter ha eliminerat integralen i z-led går över till polära koordinater med 0≤r≤1/sqrt(2) och 0≤theta≤2π, eller så går du över till rympolära med 0≤r≤1, 0≤theta≤π/4 och 0≤phi≤2π.
Vilken metod vill du använda så skall vi försöka lotsa dig fram (vid behov).
Trinity2 skrev:destiny99 skrev:Trinity2 skrev:destiny99 skrev:Trinity2 skrev:
Under glasstruten har vi x^2+y^2+z^2<=1 menar du? Men isåfall har vi området x^2+y^2<=1 för xy planet och z går från 0 till sqrt(x^2+y^2)? Hur påverkas gränserna för vinkel t för polära koordinater byte? Är det fortfarande 0 till 2pi?
Jag tror det blir enklare om man går över till rympolära koordinater och anger de r, theta och phi som definierar glasstruten. Man kan räkna som du gör också, men då skall z gå från sqrt(x^2+y^2) till sqrt(1-(x^2+y^2)) och det gäller att tänka på övre begränsning för x^2+y^2. (Konen är 45°-kon så skärning med sfären sker ej då x^2+y^2=1.)
Här är en enkel och tydlig beskrivning på rymdpolärt koordinatbyte
https://courses.mai.liu.se/GU/TATA69/M/presentationer/teori11del2.pdf
Ja precis! Jag får fortfarande inte rätt svar dock. Så med vilka gränser varierar r då om vinkeln går mellan 0 till pi/4
Jag tror du rör ihop begreppen en aning.
Antingen så arbetar du i xy-planet med 0≤x^2+y^2≤1/sqrt(2) och efter ha eliminerat integralen i z-led går över till polära koordinater med 0≤r≤1/sqrt(2) och 0≤theta≤2π, eller så går du över till rympolära med 0≤r≤1, 0≤theta≤π/4 och 0≤phi≤2π.
Vilkan metod vill du använda så skall vi försöka lotsa dig fram (vid behov).
Jag tänkte fortsätta med min metod och går över till rymdpolära koordinater i andra frågor. Annars blir det bara rörigt pendla mellan dessa två metoder. Så vi kan gärna fortsätta där jag är justnu med min nuvarande metod och se vad jag behöver rätta till så gör jag det
destiny99 skrev:Trinity2 skrev:destiny99 skrev:Trinity2 skrev:destiny99 skrev:Trinity2 skrev:
Under glasstruten har vi x^2+y^2+z^2<=1 menar du? Men isåfall har vi området x^2+y^2<=1 för xy planet och z går från 0 till sqrt(x^2+y^2)? Hur påverkas gränserna för vinkel t för polära koordinater byte? Är det fortfarande 0 till 2pi?
Jag tror det blir enklare om man går över till rympolära koordinater och anger de r, theta och phi som definierar glasstruten. Man kan räkna som du gör också, men då skall z gå från sqrt(x^2+y^2) till sqrt(1-(x^2+y^2)) och det gäller att tänka på övre begränsning för x^2+y^2. (Konen är 45°-kon så skärning med sfären sker ej då x^2+y^2=1.)
Här är en enkel och tydlig beskrivning på rymdpolärt koordinatbyte
https://courses.mai.liu.se/GU/TATA69/M/presentationer/teori11del2.pdf
Ja precis! Jag får fortfarande inte rätt svar dock. Så med vilka gränser varierar r då om vinkeln går mellan 0 till pi/4
Jag tror du rör ihop begreppen en aning.
Antingen så arbetar du i xy-planet med 0≤x^2+y^2≤1/sqrt(2) och efter ha eliminerat integralen i z-led går över till polära koordinater med 0≤r≤1/sqrt(2) och 0≤theta≤2π, eller så går du över till rympolära med 0≤r≤1, 0≤theta≤π/4 och 0≤phi≤2π.
Vilkan metod vill du använda så skall vi försöka lotsa dig fram (vid behov).
Jag tänkte fortsätta med min metod och går över till rymdpolära koordinater i andra frågor. Annars blir det bara rörigt pendla mellan dessa två metoder.
OK, då stannar vi i xy-planet. z rör sig mellan sqrt(x^2+y^2) och sqrt(1-(x^2+y^2)) för något talpar (x,y) som vi inte behöver bry oss om nu. Kan du eliminera integralen i z-led?
Trinity2 skrev:destiny99 skrev:Trinity2 skrev:destiny99 skrev:Trinity2 skrev:destiny99 skrev:Trinity2 skrev:
Under glasstruten har vi x^2+y^2+z^2<=1 menar du? Men isåfall har vi området x^2+y^2<=1 för xy planet och z går från 0 till sqrt(x^2+y^2)? Hur påverkas gränserna för vinkel t för polära koordinater byte? Är det fortfarande 0 till 2pi?
Jag tror det blir enklare om man går över till rympolära koordinater och anger de r, theta och phi som definierar glasstruten. Man kan räkna som du gör också, men då skall z gå från sqrt(x^2+y^2) till sqrt(1-(x^2+y^2)) och det gäller att tänka på övre begränsning för x^2+y^2. (Konen är 45°-kon så skärning med sfären sker ej då x^2+y^2=1.)
Här är en enkel och tydlig beskrivning på rymdpolärt koordinatbyte
https://courses.mai.liu.se/GU/TATA69/M/presentationer/teori11del2.pdf
Ja precis! Jag får fortfarande inte rätt svar dock. Så med vilka gränser varierar r då om vinkeln går mellan 0 till pi/4
Jag tror du rör ihop begreppen en aning.
Antingen så arbetar du i xy-planet med 0≤x^2+y^2≤1/sqrt(2) och efter ha eliminerat integralen i z-led går över till polära koordinater med 0≤r≤1/sqrt(2) och 0≤theta≤2π, eller så går du över till rympolära med 0≤r≤1, 0≤theta≤π/4 och 0≤phi≤2π.
Vilkan metod vill du använda så skall vi försöka lotsa dig fram (vid behov).
Jag tänkte fortsätta med min metod och går över till rymdpolära koordinater i andra frågor. Annars blir det bara rörigt pendla mellan dessa två metoder.
OK, då stannar vi i xy-planet. z rör sig mellan sqrt(x^2+y^2) och sqrt(1-(x^2+y^2)) för något talpar (x,y) som vi inte behöver bry oss om nu. Kan du eliminera integralen i z-led?
Yes jag skrev ju om sqrt(x^2+y^2) och roten ur (1-r^2)som sqrt(r) i någon av mina lösningar. Jag antar att man inte får göra så?
destiny99 skrev:Trinity2 skrev:destiny99 skrev:Trinity2 skrev:destiny99 skrev:Trinity2 skrev:destiny99 skrev:Trinity2 skrev:
Under glasstruten har vi x^2+y^2+z^2<=1 menar du? Men isåfall har vi området x^2+y^2<=1 för xy planet och z går från 0 till sqrt(x^2+y^2)? Hur påverkas gränserna för vinkel t för polära koordinater byte? Är det fortfarande 0 till 2pi?
Jag tror det blir enklare om man går över till rympolära koordinater och anger de r, theta och phi som definierar glasstruten. Man kan räkna som du gör också, men då skall z gå från sqrt(x^2+y^2) till sqrt(1-(x^2+y^2)) och det gäller att tänka på övre begränsning för x^2+y^2. (Konen är 45°-kon så skärning med sfären sker ej då x^2+y^2=1.)
Här är en enkel och tydlig beskrivning på rymdpolärt koordinatbyte
https://courses.mai.liu.se/GU/TATA69/M/presentationer/teori11del2.pdf
Ja precis! Jag får fortfarande inte rätt svar dock. Så med vilka gränser varierar r då om vinkeln går mellan 0 till pi/4
Jag tror du rör ihop begreppen en aning.
Antingen så arbetar du i xy-planet med 0≤x^2+y^2≤1/sqrt(2) och efter ha eliminerat integralen i z-led går över till polära koordinater med 0≤r≤1/sqrt(2) och 0≤theta≤2π, eller så går du över till rympolära med 0≤r≤1, 0≤theta≤π/4 och 0≤phi≤2π.
Vilkan metod vill du använda så skall vi försöka lotsa dig fram (vid behov).
Jag tänkte fortsätta med min metod och går över till rymdpolära koordinater i andra frågor. Annars blir det bara rörigt pendla mellan dessa två metoder.
OK, då stannar vi i xy-planet. z rör sig mellan sqrt(x^2+y^2) och sqrt(1-(x^2+y^2)) för något talpar (x,y) som vi inte behöver bry oss om nu. Kan du eliminera integralen i z-led?
Yes jag skrev ju om sqrt(x^2+y^2) och roten ur (1-r^2)som sqrt(r) i någon av mina lösningar. Jag antar att man inte får göra så?
Ja, men du räknar så snabbt i huvet och inför variabler lite fort att det blir fel på vägen. Ta det lugnt och skriv ut varje steg.
Trinity2 skrev:destiny99 skrev:Trinity2 skrev:destiny99 skrev:Trinity2 skrev:destiny99 skrev:Trinity2 skrev:destiny99 skrev:Trinity2 skrev:
Under glasstruten har vi x^2+y^2+z^2<=1 menar du? Men isåfall har vi området x^2+y^2<=1 för xy planet och z går från 0 till sqrt(x^2+y^2)? Hur påverkas gränserna för vinkel t för polära koordinater byte? Är det fortfarande 0 till 2pi?
Jag tror det blir enklare om man går över till rympolära koordinater och anger de r, theta och phi som definierar glasstruten. Man kan räkna som du gör också, men då skall z gå från sqrt(x^2+y^2) till sqrt(1-(x^2+y^2)) och det gäller att tänka på övre begränsning för x^2+y^2. (Konen är 45°-kon så skärning med sfären sker ej då x^2+y^2=1.)
Här är en enkel och tydlig beskrivning på rymdpolärt koordinatbyte
https://courses.mai.liu.se/GU/TATA69/M/presentationer/teori11del2.pdf
Ja precis! Jag får fortfarande inte rätt svar dock. Så med vilka gränser varierar r då om vinkeln går mellan 0 till pi/4
Jag tror du rör ihop begreppen en aning.
Antingen så arbetar du i xy-planet med 0≤x^2+y^2≤1/sqrt(2) och efter ha eliminerat integralen i z-led går över till polära koordinater med 0≤r≤1/sqrt(2) och 0≤theta≤2π, eller så går du över till rympolära med 0≤r≤1, 0≤theta≤π/4 och 0≤phi≤2π.
Vilkan metod vill du använda så skall vi försöka lotsa dig fram (vid behov).
Jag tänkte fortsätta med min metod och går över till rymdpolära koordinater i andra frågor. Annars blir det bara rörigt pendla mellan dessa två metoder.
OK, då stannar vi i xy-planet. z rör sig mellan sqrt(x^2+y^2) och sqrt(1-(x^2+y^2)) för något talpar (x,y) som vi inte behöver bry oss om nu. Kan du eliminera integralen i z-led?
Yes jag skrev ju om sqrt(x^2+y^2) och roten ur (1-r^2)som sqrt(r) i någon av mina lösningar. Jag antar att man inte får göra så?
Ja, men du räknar så snabbt i huvet och inför variabler lite fort att det blir fel på vägen. Ta det lugnt och skriv ut varje steg.
Ah sorry jag började först integrera först map på z och de gränserna vi pratat om som den är emellan. Här är resultatet jag fick.

Inte så dumt, kan du skriva om det lite till så vi får "x^2+y^2" som "grupp" överallt?
Trinity2 skrev:Inte så dumt, kan du skriva om det lite till så vi får "x^2+y^2" som "grupp" överallt?
Hur då omskrivning?
Detta
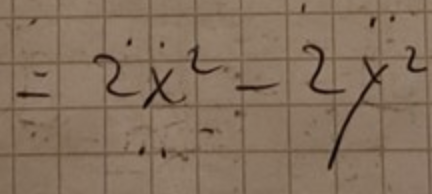
kan "förbättras"
Trinity2 skrev:Detta
kan "förbättras"
Ah såhär långt kom jag med min omskrivning.

Mkt bra!
Du bör nu ha en integral

Trinity2 skrev:Mkt bra!
Du bör nu ha en integral
Ja precis men gränserna för x och y. Kan man möjligen gå över till polära? Hur blir det med gränserna i denna kon?
destiny99 skrev:Trinity2 skrev:Mkt bra!
Du bör nu ha en integral
Ja precis men gränserna för x och y. Kan man möjligen gå över till polära? Hur blir det med gränserna i denna kon?
Ja, det är nästa steg, att gå över till polära i planet. Vi börjar med att skriva om integranden och funderar på gränserna senare. Vad blir den "polära integralen" (utan några gränser just nu)?
Trinity2 skrev:destiny99 skrev:Trinity2 skrev:Mkt bra!
Du bör nu ha en integral
Ja precis men gränserna för x och y. Kan man möjligen gå över till polära? Hur blir det med gränserna i denna kon?
Ja, det är nästa steg, att gå över till polära i planet. Vi börjar med att skriva om integranden och funderar på gränserna senare. Vad blir den "polära integralen" (utan några gränser just nu)?
Om man sätter x=rcost och y=rsint så får jag följande:

Tillägg: 14 feb 2025 17:07
Lyckades lösa integralen mha gränserna för r som är mellan 0 och 1/sqrt(2) och vinkeln mellan 0 och 2pi. Dock förstår jag inte varför vinkeln ska vara mellan 0 och 2pi (ser typ ej det i figuren). Men dessa gav iaf rätt svar.
(x,y) befinner sig på cirkelskivan x^2+y^2≤2 varför 0≤theta≤2π, annars blir det ej en hel cirkelskiva.
Trinity2 skrev:(x,y) befinner sig på cirkelskivan x^2+y^2≤2 varför 0≤theta≤2π, annars blir det ej en hel cirkelskiva.
Var kommer 2an ifrån i HL? Ska det inte vara x^2+y^2<=1/2?
destiny99 skrev:Trinity2 skrev:(x,y) befinner sig på cirkelskivan x^2+y^2≤2 varför 0≤theta≤2π, annars blir det ej en hel cirkelskiva.
Var kommer 2an ifrån i HL? Ska det inte vara x^2+y^2<=1/2?
Självklart skall det vara det! Mitt fel! Jag måste ha lite mat för att förse hjärnan med energi märker jag...