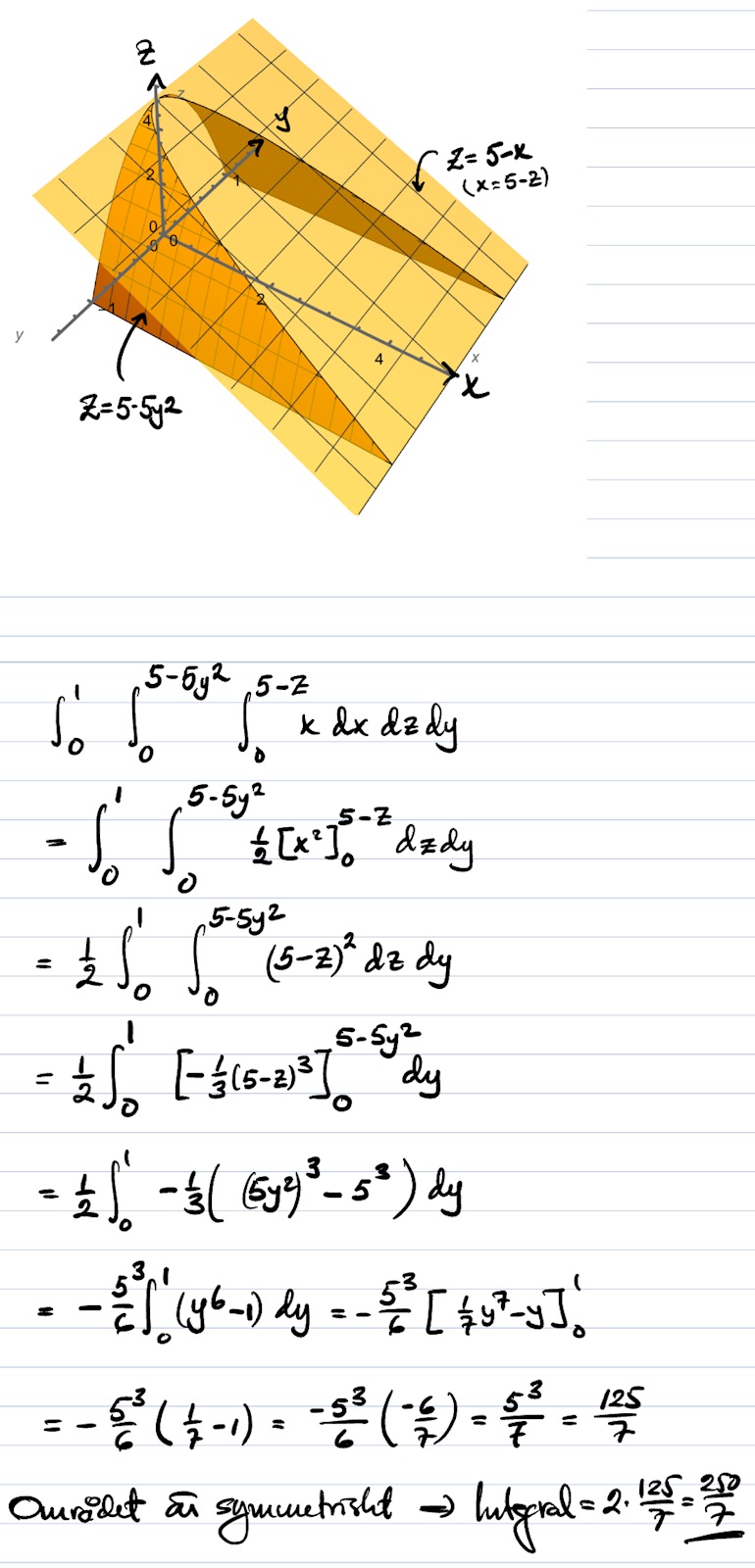Trippelintegral - område begränsat av en parabolisk cylinder
Jag trodde att jag förstod hur man löste trippelintegraler men tydligen inte. Får till en uppställning men den är så bedrövlig att jag börjar gråta halvvägs igenom. Det måste finnas lättare sätt att ställa upp det än
Ni får gärna också förklara tankesättet för lösning av trippelint. Nu har jag försökt lösa det genom att jag ställer upp en variabel med gränser som beror på de två andra variablerna, löser den integralen och sedan ser projektionen på de övriga variablerna som ett nytt område att integrera över.
Det du har ställt upp fungerar bra. När man jobbar med trippelintegraler kan det bli VÄLDIGT mycket räknande och många möjligheter för räknefel. Alltid när man löser dubbel- och trippelintegraler så vill man ha en ide över hur området ser ut vilket hjälper till när man ska bestämma integrationsgränserna. Det kan hjälpa att rita hur figuren ser ut från olika sidor. T.ex i den här uppgiften om vi kollar på figuren i yz-planet ser den ut på följande sätt: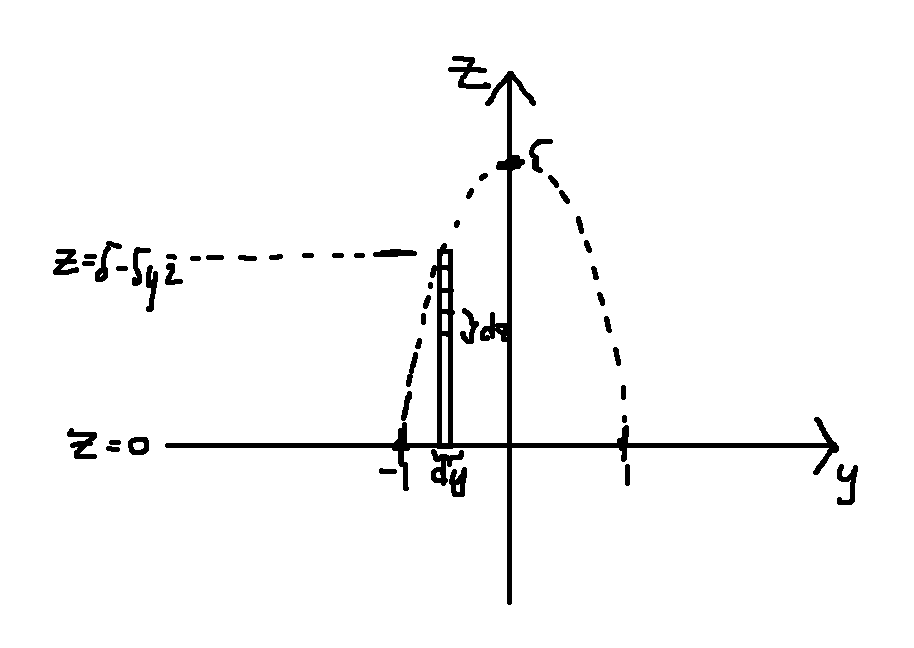 
Då ser vi tydligt att vi kan ställa upp gränser för den ytan. Sedan vet vi att ytan x = 5 - z begränsar området uppifrån och då kan vi lägga till gränsen från 0 till 5 - z map. x.
Som sagt, uppställningen ser bra ut, frågan blir mer om den kan lösas på ett snyggt sätt. Kanske finns det något variabelbyte man kan införa? Annars är den inte superkomplicerad. Det jobbigaste man behöver göra är att utveckla (5 - 5y^2)^3. Hoppas detta hjälper något, det var ett tag sen jag läste flervarren så är lite rostig :)
Edit: glömde nämna att man kan kolla på hur något tvärsnitt av området ser ut och hur det förändras genom området.
Ja, okej. Då har jag nog förstått. Jag får nog bara acceptera att lite räkning krävs för dessa uppgifter.. hehe.
MrPotatohead skrev:Ja, okej. Då har jag nog förstått. Jag får nog bara acceptera att lite räkning krävs för dessa uppgifter.. hehe.
Förslag på räkning som är hyfsat överkomlig hoppas jag
Trinity2 skrev:MrPotatohead skrev:Ja, okej. Då har jag nog förstått. Jag får nog bara acceptera att lite räkning krävs för dessa uppgifter.. hehe.
Förslag på räkning som är hyfsat överkomlig hoppas jag
Wow vilken snygg figur, är det i GeoGebra eller något helt annat?
