Två av kvadratens sidor ligger på de positiva koordinataxlarna… (A-nivå) (Matematik/Matte 2/Funktioner och grafer)

Hej.

Du beräknar funktionens nollställen, dvs de punkter där parabeln skär x-axeln.

Men den informationen har du ingen nytta av.

Försök istället att använda det faktum att ett av kvadratens hörn ligger på parabeln, vilket innebär att detta hörns koordinater (x, y) uppfyller sambandet y = 19,25+3x-x².

Sedan finns det även ett annat användbart samband mellan x och y, som hänger ihop med att det är en kvadrat.

maratmatorkin skrev:
Behöver hjälp.

Så har jag aldrig sett det. Jag tycker att det inte ser bra ut, och jag skulle rekommendera att du inte skriver så.

Yngve skrev:
Hej.

Du beräknar funktionens nollställen, dvs de punkter där parabeln skär x-axeln.

Men den informationen har du ingen nytta av.

Försök istället att använda det faktum att ett av kvadratens hörn ligger på parabeln, vilket innebär att detta hörns koordinater (x, y) uppfyller sambandet y = 19,25+3x-x².

Sedan finns det även ett annat användbart samband mellan x och y, som hänger ihop med att det är en kvadrat.

Ok. Det var lite så jag tänkte och började fundera på avståndsformeln. Nyss tänkte jag så. Men tror det också är fel.

Pieter Kuiper skrev:
maratmatorkin skrev:
Behöver hjälp.

Så har jag aldrig sett det. Jag tycker att det inte ser bra ut, och jag skulle rekommendera att du inte skriver så.

Ok, tack! Alltså likhetstecken under roten menar du?

Kan du förklara varför du löser ekvationen -x²+3x+19,25 = 0?

Yngve skrev:
Kan du förklara varför du löser ekvationen -x²+3x+19,25 = 0?

För att jag inte ska behöva göra något i HL. Tänker nog fel där.

maratmatorkin skrev:
Pieter Kuiper skrev:
maratmatorkin skrev:
Behöver hjälp.

Så har jag aldrig sett det. Jag tycker att det inte ser bra ut, och jag skulle rekommendera att du inte skriver så.

Ok, tack! Alltså likhetstecken under roten menar du?

Ja, det är inte standard.

(Det kan vara så att du hade en lärare eller en Youtuber som gör så, men det ser inte alls bra ut.)

maratmatorkin skrev:

För att jag inte ska behöva göra något i HL. Tänker nog fel där.

Vilket högerled?

Bilden visar en parabel som beskrivs av en funktion y = -x²+3x+19,25.

När du löser ekvationen -x²+3x+19,25 = 0 så kommer du att få fram funktionens nollställen, dvs x-koordinaterna för de punkter där parabeln skär x-axeln.

Jag har markerat dessa punkter i blått och kallat dem A och B i bilden.

Vad tänkte du att du ska göra med den informationen?

Yngve skrev:
maratmatorkin skrev:

För att jag inte ska behöva göra något i HL. Tänker nog fel där.

Vilket högerled?

Bilden visar en parabel som beskrivs av en funktion y = -x²+3x+19,25.

När du löser ekvationen -x²+3x+19,25 = 0 så kommer du att få fram funktionens nollställen, dvs x-koordinaterna för de punkter där parabeln skär x-axeln.

Jag har markerat dessa punkter i blått och kallat dem A och B i bilden.

Vad tänkte du att du ska göra med den informationen?

Inget. Vilket jag redan demonstrerat högst upp med "D". :)

Pieter Kuiper skrev:
maratmatorkin skrev:
Pieter Kuiper skrev:
maratmatorkin skrev:
Behöver hjälp.

Så har jag aldrig sett det. Jag tycker att det inte ser bra ut, och jag skulle rekommendera att du inte skriver så.

Ok, tack! Alltså likhetstecken under roten menar du?

Ja, det är inte standard.

(Det kan vara så att du hade en lärare eller en Youtuber som gör så, men det ser inte alls bra ut.)

Jag började göra så själv för att det sparar mig bördan att behöva skriva om det mesta på nästa rad bara för att visuellt visa att de är likvärdiga. :)

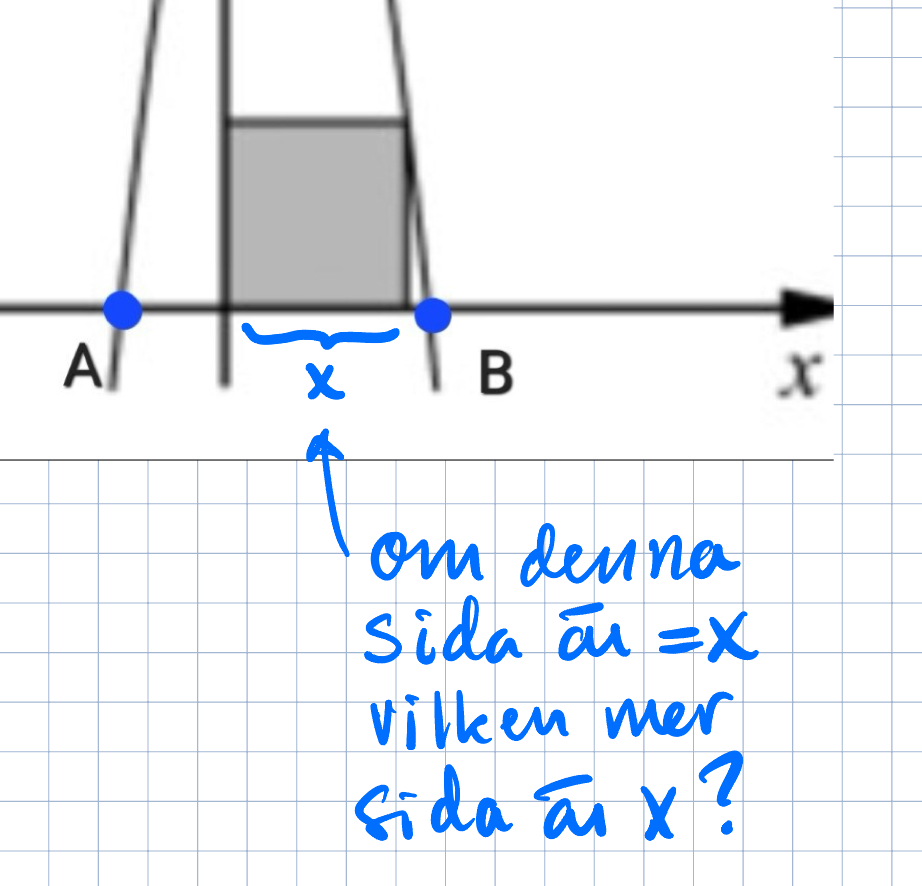
Om du låter kvadraten ha sidan x. vad kan du säga om höjden längs y-axeln? Hur lång är den?

Kan du finna en till vertikal sträcka som är lika lång?

Trinity2 skrev:
Om du låter kvadraten ha sidan x. vad kan du säga om höjden längs y-axeln? Hur lång är den?

Kan du finna en till vertikal sträcka som är lika lång?

Precis. Även ritat upp detta högst upp. Tänkte lite i banorna att avståndsformeln borde ge mig nåt? Kanske (x, y)^2? Dvs x^2 + x^2. I en uppgift såg jag att (x, y)^2 tolkas som x + y. Vet ej varför det blir så. Men vi ser ju exempelvis (x, 0). Sedan (0, x)...

Punkten C har koordinaterna (x, y).

Eftersom punkten C ligger på parabeln så uppfyller dessa koordinater sambandet y = -x²+3x+19,25.

Är du med på det?

Sedan finns det även ett annar, enklare samband mellan x och y. Detta enklare samband hänger ihop med att C är ett hörn i en kvadrat.

maratmatorkin skrev:
Trinity2 skrev:
Om du låter kvadraten ha sidan x. vad kan du säga om höjden längs y-axeln? Hur lång är den?

Kan du finna en till vertikal sträcka som är lika lång?

Precis. Även ritat upp detta högst upp. Tänkte lite i banorna att avståndsformeln borde ge mig nåt? Kanske (x, y)^2? Dvs x^2 + x^2. I en uppgift såg jag att (x, y)^2 tolkas som x + y. Vet ej varför det blir så. Men vi ser ju exempelvis (x, 0). Sedan (0, x)...

Yngve skrev:
Punkten C har koordinaterna (x, y).

Eftersom punkten C ligger på parabeln så uppfyller dessa koordinater sambandet y = -x²+3x+19,25.

Är du med på det?

Sedan finns det även ett annar, enklare samband mellan x och y. Detta enklare samband hänger ihop med att C är ett hörn i en kvadrat.

:D C ja, haha. En sekund, måste börja skissa.

Trinity2 skrev:
maratmatorkin skrev:
Trinity2 skrev:
Om du låter kvadraten ha sidan x. vad kan du säga om höjden längs y-axeln? Hur lång är den?

Kan du finna en till vertikal sträcka som är lika lång?

Precis. Även ritat upp detta högst upp. Tänkte lite i banorna att avståndsformeln borde ge mig nåt? Kanske (x, y)^2? Dvs x^2 + x^2. I en uppgift såg jag att (x, y)^2 tolkas som x + y. Vet ej varför det blir så. Men vi ser ju exempelvis (x, 0). Sedan (0, x)...

Alla givetvis. Det är ju en kvadrat.. :)

Yngve skrev:
Punkten C har koordinaterna (x, y).

Eftersom punkten C ligger på parabeln så uppfyller dessa koordinater sambandet y = -x²+3x+19,25.

Är du med på det?

Sedan finns det även ett annar, enklare samband mellan x och y. Detta enklare samband hänger ihop med att C är ett hörn i en kvadrat.

Kan detta stämma? Får dock inte att y=19,25

maratmatorkin skrev:
Yngve skrev:
Punkten C har koordinaterna (x, y).

Eftersom punkten C ligger på parabeln så uppfyller dessa koordinater sambandet y = -x²+3x+19,25.

Är du med på det?

Sedan finns det även ett annar, enklare samband mellan x och y. Detta enklare samband hänger ihop med att C är ett hörn i en kvadrat.

Kan detta stämma? Får dock inte att y=19,25

Parabeln tangerar kvadraten vid x (kvadratens sida)

Då parabeln tangerar vid x, kan du stoppa y=x, dvs -x^2 +3x +19,25=x

Lös sedan för X genom att få över alla termer till en sida och stoppa HL=0.

Att ta reda på nollställen här kommer inte vara relevant, då du endast vill ta reda på hur parabeln förhåller sig till själva kvadraten.

maratmatorkin skrev:

Kan detta stämma? Får dock inte att y=19,25

Nej, det stämmer inte.

Om f(x) = -x²+3x+19,25 så ger

f(0) y-koordinaten för parabelns skärningspunkt med y-axeln, dvs y = 19,25.
f(19,25) y-koordinaten för den punkt på parabeln där x-värdet är 19,25., dvs y = -293.5625.

Ingen av dessa punkter har något med kvadraten att göra.

Tanken med de ledtrådar jag gav var att de skulle leda fram till att det för punkten C med koordinaterna (x, y) gäller att

y = -x²+3x+19,25 (eftersom punkten ligger på parabeln)
y = x (eftersom kvadratens sidor är lika långa)

Detta är ett ekvationssystem med två ekvationer. Du kan lösa det med metoden som aaaa1111 beskrev. Lösningen till ekvationssystemet ger dig kvadratens sidlängd.

Det viktiga här är att du förstår varför de två ekvationerna gäller vid punkt C.

Yngve skrev:
maratmatorkin skrev:

Kan detta stämma? Får dock inte att y=19,25

Nej, det stämmer inte.

Om f(x) = -x²+3x+19,25 så ger

f(0) y-koordinaten för parabelns skärningspunkt med y-axeln, dvs y = 19,25.

f(19,25) y-koordinaten för den punkt på parabeln där x-värdet är 19,25., dvs y = -293.5625.

Ingen av dessa punkter har något med kvadraten att göra.

Tanken med de ledtrådar jag gav var att de skulle leda fram till att det för punkten C med koordinaterna (x, y) gäller att

y = -x²+3x+19,25 (eftersom punkten ligger på parabeln)

y = x (eftersom kvadratens sidor är lika långa)

Detta är ett ekvationssystem med två ekvationer. Du kan lösa det med metoden som aaaa1111 beskrev. Lösningen till ekvationssystemet ger dig kvadratens sidlängd.

Det viktiga här är att du förstår varför de två ekvationerna gäller vid punkt C.

Tack Yngve! Tänker över frukosten vad ni menar. Återkommer.

maratmatorkin skrev:

Tack Yngve! Tänker över frukosten vad ni menar. Återkommer.

OK bra.

Rätta mig om jag har fel, men det verkar som att du bara räknar, utan att egentligen veta vad det är du räknar eller varför du gör det.

====

I så fall tror jag att du har mycket att tjäna på att öka förståelsen för hur saker hänger ihop, t.ex. kopplingen mellan ett funktionsuttryck och motsvarande graf (i det här fallet en andragradsfunktion och en parabel).

Säg till om det är vissa partier i din lärobok som du tycker är svåra att förstå. I så fall kan vi hjälpa dig med detta.

Yngve skrev:
maratmatorkin skrev:

Tack Yngve! Tänker över frukosten vad ni menar. Återkommer.

OK bra.

Rätta mig om jag har fel, men det verkar som att du bara räknar, utan att egentligen veta vad det är du räknar eller varför du gör det.

====

I så fall tror jag att du har mycket att tjäna på att öka förståelsen för hur saker hänger ihop, t.ex. kopplingen mellan ett funktionsuttryck och motsvarande graf (i det här fallet en andragradsfunktion och en parabel).

Säg till om det är vissa partier i din lärobok som du tycker är svåra att förstå. I så fall kan vi hjälpa dig med detta.

Ibland.. klargjorde kvadratrotsmetoden igår på Eddler. I boken 5000 2012 var förklaringen sådär.

Jag har ju koll på nollställen (iaf den korta period jag kunnat det), parabel, glad/ledsen gubbe (koefficienten i ’ax’), symmetrilinjen (högsta/minsta y-värde där x = -(b/2a), vad de olika koefficienterna gör grafiskt, t ex c i ax+bx+c (flyttas upp och ned) etc. Sen glömmer jag vissa delar så har väl inte skapats alla banor i minnescellerna/nervbanorna ännu; vilket kräver repetition. I panik testar jag gå på intuition genom att testa olika saker. Ibland fungerar det; oftast inte.

Ja, jag behöver hjälp med det mesta i livet.

maratmatorkin skrev:

Ibland.. klargjorde kvadratrotsmetoden igår på Eddler. I boken 5000 2012 var förklaringen sådär.

Bra att du söker andra källor om din bok inte lyckas förklara tillräckligt bra.

Jag har ju koll på nollställen (iaf den korta period jag kunnat det), parabel, glad/ledsen gubbe (koefficienten i ’ax’), symmetrilinjen (högsta/minsta y-värde där x = -(b/2a), vad de olika koefficienterna gör grafiskt, t ex c i ax+bx+c (flyttas upp och ned) etc.

Utmärkt. Har du även koll på sambandet mellan funktionsuttryck och funktionsgraf?

Exempel, säg att vi har en andragradsfunktion y = 3x²×5x-12 och att vi har ritat motsvarande parabel i ett koordinatsystem.

Då gäller följande:

Alla punkter (x, y) som ligger på parabeln uppfyller sambandet y = 3x²+5x-12
Alla punkter (x, y) som uppfyller sambandet y = 3x²+5x-12 ligger på parabeln.

Detta är inte unikt för andragradsfunktioner utan det gäller för alla funktioner med tillhörande grafer.

Sen glömmer jag vissa delar så har väl inte skapats alla banor i minnescellerna/nervbanorna ännu; vilket kräver repetition. I panik testar jag gå på intuition genom att testa olika saker. Ibland fungerar det; oftast inte.

OK, det förklarar saken. En positiv sak är att ju fler uppgifter du räknar, desto mer kommer minnescelleena/nervbanorna att vänja sig vid detta och det blir lättare för dig att se mönster och öka chanserna att påbörja en lösning på ett framkomlig sätt.

Ja, jag behöver hjälp med det mesta i livet.

Tack för att du vågar dela. Det underlättar för alla hjälpare att anpassa hjälpen på rätt sätt. Jag rekommenderar dig att ställa följdfrågor när du är osäker på vad du ska göra med de tips och råd som du får i trådarna här.

Yngve skrev:
maratmatorkin skrev:

Ibland.. klargjorde kvadratrotsmetoden igår på Eddler. I boken 5000 2012 var förklaringen sådär.

Bra att du söker andra källor om din bok inte lyckas förklara tillräckligt bra.

Jag har ju koll på nollställen (iaf den korta period jag kunnat det), parabel, glad/ledsen gubbe (koefficienten i ’ax’), symmetrilinjen (högsta/minsta y-värde där x = -(b/2a), vad de olika koefficienterna gör grafiskt, t ex c i ax+bx+c (flyttas upp och ned) etc.

Utmärkt. Har du även koll på sambandet mellan funktionsuttryck och funktionsgraf?

Exempel, säg att vi har en andragradsfunktion y = 3x²×5x-12 och att vi har ritat motsvarande parabel i ett koordinatsystem.

Då gäller följande:

Alla punkter (x, y) som ligger på parabeln uppfyller sambandet y = 3x²+5x-12

Alla punkter (x, y) som uppfyller sambandet y = 3x²+5x-12 ligger på parabeln.

Detta är inte unikt för andragradsfunktioner utan det gäller för alla funktioner med tillhörande grafer.

Sen glömmer jag vissa delar så har väl inte skapats alla banor i minnescellerna/nervbanorna ännu; vilket kräver repetition. I panik testar jag gå på intuition genom att testa olika saker. Ibland fungerar det; oftast inte.

OK, det förklarar saken. En positiv sak är att ju fler uppgifter du räknar, desto mer kommer minnescelleena/nervbanorna att vänja sig vid detta och det blir lättare för dig att se mönster och öka chanserna att påbörja en lösning på ett framkomlig sätt.

Ja, jag behöver hjälp med det mesta i livet.

Tack för att du vågar dela. Det underlättar för alla hjälpare att anpassa hjälpen på rätt sätt. Jag rekommenderar dig att ställa följdfrågor när du är osäker på vad du ska göra med de tips och råd som du får i trådarna här.

”

f(0) y-koordinaten för parabelns skärningspunkt med y-axeln, dvs y = 19,25.”

så är det givetvis, ja! Vet inte hur jag tänkte igår.

”OK, det förklarar saken. En positiv sak är att ju fler uppgifter du räknar, desto mer kommer minnescelleena/nervbanorna att vänja sig vid detta och det blir lättare för dig att se mönster och öka chanserna att påbörja en lösning på ett framkomlig sätt.”

det och 100 andra saker.

Ja! Precis som du säger så ger övning färdighet. Det är därför jag envisas med A-frågor vilket antingen kommer brista, eller bära; bli min undergång, eller bästa vän.

”

Tack för att du vågar dela. Det underlättar för alla hjälpare att anpassa hjälpen på rätt sätt. Jag rekommenderar dig att ställa följdfrågor när du är osäker på vad du ska göra med de tips och råd som du får i trådarna här.”

tack för tipsen. Ska ha det i åtanke. Återkommer när jag löst uppgiften eller har följdfrågor.

Alla punkter (x, y) som ligger på parabeln uppfyller sambandet y = 3x²+5x-12

Alla punkter (x, y) som uppfyller sambandet y = 3x²+5x-12 ligger på parabeln.

Ekvivalens?😁

Yngve skrev:
maratmatorkin skrev:

Kan detta stämma? Får dock inte att y=19,25

Nej, det stämmer inte.

Om f(x) = -x²+3x+19,25 så ger

f(0) y-koordinaten för parabelns skärningspunkt med y-axeln, dvs y = 19,25.

f(19,25) y-koordinaten för den punkt på parabeln där x-värdet är 19,25., dvs y = -293.5625.

Ingen av dessa punkter har något med kvadraten att göra.

Tanken med de ledtrådar jag gav var att de skulle leda fram till att det för punkten C med koordinaterna (x, y) gäller att

y = -x²+3x+19,25 (eftersom punkten ligger på parabeln)

y = x (eftersom kvadratens sidor är lika långa)

Detta är ett ekvationssystem med två ekvationer. Du kan lösa det med metoden som aaaa1111 beskrev. Lösningen till ekvationssystemet ger dig kvadratens sidlängd.

Det viktiga här är att du förstår varför de två ekvationerna gäller vid punkt C.

Korrekt? Jag fixade även till min kvadratkomplettering så att den nu är korrekt 🙂 Nu förstår jag kvadratkomplettering dessutom. Tyckte väl jag hade missförstått något.

Tack för allas visade tålamod🙏

Pieter Kuiper skrev:
maratmatorkin skrev:
Pieter Kuiper skrev:
maratmatorkin skrev:
Behöver hjälp.

Så har jag aldrig sett det. Jag tycker att det inte ser bra ut, och jag skulle rekommendera att du inte skriver så.

Ok, tack! Alltså likhetstecken under roten menar du?

Ja, det är inte standard.

(Det kan vara så att du hade en lärare eller en Youtuber som gör så, men det ser inte alls bra ut.)

Och Pieter, jag hittade ett exempel som du kanske menar vore bättre.

maratmatorkin skrev:

Alla punkter (x, y) som ligger på parabeln uppfyller sambandet y = 3x²+5x-12

Alla punkter (x, y) som uppfyller sambandet y = 3x²+5x-12 ligger på parabeln.

Ekvivalens?😁

Yngve skrev:
maratmatorkin skrev:

Kan detta stämma? Får dock inte att y=19,25

Nej, det stämmer inte.

Om f(x) = -x²+3x+19,25 så ger

f(0) y-koordinaten för parabelns skärningspunkt med y-axeln, dvs y = 19,25.

f(19,25) y-koordinaten för den punkt på parabeln där x-värdet är 19,25., dvs y = -293.5625.

Ingen av dessa punkter har något med kvadraten att göra.

Tanken med de ledtrådar jag gav var att de skulle leda fram till att det för punkten C med koordinaterna (x, y) gäller att

y = -x²+3x+19,25 (eftersom punkten ligger på parabeln)

y = x (eftersom kvadratens sidor är lika långa)

Detta är ett ekvationssystem med två ekvationer. Du kan lösa det med metoden som aaaa1111 beskrev. Lösningen till ekvationssystemet ger dig kvadratens sidlängd.

Det viktiga här är att du förstår varför de två ekvationerna gäller vid punkt C.

Korrekt? Jag fixade även till min kvadratkomplettering så att den nu är korrekt 🙂 Nu förstår jag kvadratkomplettering dessutom. Tyckte väl jag hade missförstått något.

Tack för allas visade tålamod🙏

Det ser bra ut! Glöm inte att exkludera den negativa lösningen sen, jag fick lära mig det den hårda vägen genom poängavdrag på prov..

Förstår du stegen, dvs teorin bakom det? Det är nog viktigare än själva lösningen i sig. När du förstått teorin, kommer du kunna lösa uppgifter hur lätt som helst.

aaaa1111 skrev:
maratmatorkin skrev:

Alla punkter (x, y) som ligger på parabeln uppfyller sambandet y = 3x²+5x-12

Alla punkter (x, y) som uppfyller sambandet y = 3x²+5x-12 ligger på parabeln.

Ekvivalens?😁

Yngve skrev:
maratmatorkin skrev:

Kan detta stämma? Får dock inte att y=19,25

Nej, det stämmer inte.

Om f(x) = -x²+3x+19,25 så ger

f(0) y-koordinaten för parabelns skärningspunkt med y-axeln, dvs y = 19,25.

f(19,25) y-koordinaten för den punkt på parabeln där x-värdet är 19,25., dvs y = -293.5625.

Ingen av dessa punkter har något med kvadraten att göra.

Tanken med de ledtrådar jag gav var att de skulle leda fram till att det för punkten C med koordinaterna (x, y) gäller att

y = -x²+3x+19,25 (eftersom punkten ligger på parabeln)

y = x (eftersom kvadratens sidor är lika långa)

Detta är ett ekvationssystem med två ekvationer. Du kan lösa det med metoden som aaaa1111 beskrev. Lösningen till ekvationssystemet ger dig kvadratens sidlängd.

Det viktiga här är att du förstår varför de två ekvationerna gäller vid punkt C.

Korrekt? Jag fixade även till min kvadratkomplettering så att den nu är korrekt 🙂 Nu förstår jag kvadratkomplettering dessutom. Tyckte väl jag hade missförstått något.

Tack för allas visade tålamod🙏

Det ser bra ut! Glöm inte att exkludera den negativa lösningen sen, jag fick lära mig det den hårda vägen genom poängavdrag på prov..

Förstår du stegen, dvs teorin bakom det? Det är nog viktigare än själva lösningen i sig. När du förstått teorin, kommer du kunna lösa uppgifter hur lätt som helst.

Tack för tipset. Hur gör jag det? Bara ta sudda bort den uträkningen eller lägga till den positiva roten efter ”Svar:…”

Poletten trillade ned vid x=y och ekvationssystem. Har fortfarande lite svårt för att förstå ekvationssystem i huvudet men stundtals ser jag glimtar av lösningen innan den försvinner igen.

maratmatorkin skrev:
aaaa1111 skrev:
maratmatorkin skrev:

Alla punkter (x, y) som ligger på parabeln uppfyller sambandet y = 3x²+5x-12

Alla punkter (x, y) som uppfyller sambandet y = 3x²+5x-12 ligger på parabeln.

Ekvivalens?😁

Yngve skrev:
maratmatorkin skrev:

Kan detta stämma? Får dock inte att y=19,25

Nej, det stämmer inte.

Om f(x) = -x²+3x+19,25 så ger

f(0) y-koordinaten för parabelns skärningspunkt med y-axeln, dvs y = 19,25.

f(19,25) y-koordinaten för den punkt på parabeln där x-värdet är 19,25., dvs y = -293.5625.

Ingen av dessa punkter har något med kvadraten att göra.

Tanken med de ledtrådar jag gav var att de skulle leda fram till att det för punkten C med koordinaterna (x, y) gäller att

y = -x²+3x+19,25 (eftersom punkten ligger på parabeln)

y = x (eftersom kvadratens sidor är lika långa)

Detta är ett ekvationssystem med två ekvationer. Du kan lösa det med metoden som aaaa1111 beskrev. Lösningen till ekvationssystemet ger dig kvadratens sidlängd.

Det viktiga här är att du förstår varför de två ekvationerna gäller vid punkt C.

Korrekt? Jag fixade även till min kvadratkomplettering så att den nu är korrekt 🙂 Nu förstår jag kvadratkomplettering dessutom. Tyckte väl jag hade missförstått något.

Tack för allas visade tålamod🙏

Det ser bra ut! Glöm inte att exkludera den negativa lösningen sen, jag fick lära mig det den hårda vägen genom poängavdrag på prov..

Förstår du stegen, dvs teorin bakom det? Det är nog viktigare än själva lösningen i sig. När du förstått teorin, kommer du kunna lösa uppgifter hur lätt som helst.

Tack för tipset. Hur gör jag det? Bara ta sudda bort den uträkningen eller lägga till den positiva roten efter ”Svar:…”

Poletten trillade ned vid x=y och ekvationssystem. Har fortfarande lite svårt för att förstå ekvationssystem i huvudet men stundtals ser jag glimtar av lösningen innan den försvinner igen.

Bara exkludera den roten, dvs att du vara skriver det positiva svaret! (En kvadrat kan inte ha en negativ längd ;) )

Då har du till stor del förstått teorin bakom det! Så fort jag såg att parabeln nuddade kvadratens sida tänkte jag direkt att jag stoppar de två lika med varandra, vilket brukar kunna vara ett knep på de flesta uppgifter av högre nivå.

Det handlar egentligen om att hitta genvägar och kunna visualisera dem. Ekvationssystem är klurigt men försök ta det stegvis, och fråga dig själv om det har relevans till uppgiften!

Bra jobbat igen! 😁

aaaa1111 skrev:
maratmatorkin skrev:
aaaa1111 skrev:
maratmatorkin skrev:

Alla punkter (x, y) som ligger på parabeln uppfyller sambandet y = 3x²+5x-12

Alla punkter (x, y) som uppfyller sambandet y = 3x²+5x-12 ligger på parabeln.

Ekvivalens?😁

Yngve skrev:
maratmatorkin skrev:

Kan detta stämma? Får dock inte att y=19,25

Nej, det stämmer inte.

Om f(x) = -x²+3x+19,25 så ger

f(0) y-koordinaten för parabelns skärningspunkt med y-axeln, dvs y = 19,25.

f(19,25) y-koordinaten för den punkt på parabeln där x-värdet är 19,25., dvs y = -293.5625.

Ingen av dessa punkter har något med kvadraten att göra.

Tanken med de ledtrådar jag gav var att de skulle leda fram till att det för punkten C med koordinaterna (x, y) gäller att

y = -x²+3x+19,25 (eftersom punkten ligger på parabeln)

y = x (eftersom kvadratens sidor är lika långa)

Detta är ett ekvationssystem med två ekvationer. Du kan lösa det med metoden som aaaa1111 beskrev. Lösningen till ekvationssystemet ger dig kvadratens sidlängd.

Det viktiga här är att du förstår varför de två ekvationerna gäller vid punkt C.

Korrekt? Jag fixade även till min kvadratkomplettering så att den nu är korrekt 🙂 Nu förstår jag kvadratkomplettering dessutom. Tyckte väl jag hade missförstått något.

Tack för allas visade tålamod🙏

Det ser bra ut! Glöm inte att exkludera den negativa lösningen sen, jag fick lära mig det den hårda vägen genom poängavdrag på prov..

Förstår du stegen, dvs teorin bakom det? Det är nog viktigare än själva lösningen i sig. När du förstått teorin, kommer du kunna lösa uppgifter hur lätt som helst.

Tack för tipset. Hur gör jag det? Bara ta sudda bort den uträkningen eller lägga till den positiva roten efter ”Svar:…”

Poletten trillade ned vid x=y och ekvationssystem. Har fortfarande lite svårt för att förstå ekvationssystem i huvudet men stundtals ser jag glimtar av lösningen innan den försvinner igen.

Bara exkludera den roten, dvs att du vara skriver det positiva svaret! (En kvadrat kan inte ha en negativ längd ;) )

Då har du till stor del förstått teorin bakom det! Så fort jag såg att parabeln nuddade kvadratens sida tänkte jag direkt att jag stoppar de två lika med varandra, vilket brukar kunna vara ett knep på de flesta uppgifter av högre nivå.

Det handlar egentligen om att hitta genvägar och kunna visualisera dem. Ekvationssystem är klurigt men försök ta det stegvis, och fråga dig själv om det har relevans till uppgiften!

Bra jobbat igen! 😁

🙏🙏 klarmarkerar