Två kluriga bevis...
- Bevisa att √6 är ett irrationellt tal.
- Bevisa att √3 + √2 är ett irrationellt tal
Jag har löst en liknande uppgift där det ska bevisas att √2 är ett irrationellt tal. Gäller samma princip här? I rt.ex. första delen kan jag inte bevisa att både a och b är jämna om antaget är att √2 =1,414 a/b där SGD(a,b) =1 och a/b är skrivet på enklaste form. Hur är det då två irrationella tal divideras?
Ja, visa först att 61/2 är irrationellt på sedvanligt sätt. Antag sedan att r= 31/2+21/2 är rationellt. Då är också r2= 3+2•31/2•21/2+2=5+2•61/2rationellt. Då du ovan visat att 61/2 är irrationellt så strider detta mot att såväl produkten som summan av ett rationellt tal och ett irrationellt är ett irrationellt tal. (Vilket får anses känt /annars lätt visat.) Notera dock att summan av två irrationella tal kan vara rationell.,t ex talen 61/2 och (-61/2).
Hur kan det annars bevisas: Då du ovan visat att 61/2 är irrationellt så strider detta mot att såväl produkten som summan av ett rationellt tal och ett irrationellt är ett irrationellt tal. (Vilket får anses känt /annars lätt visat.)
Låt r vara rationellt och x irrationellt och antag att summan r+x =y är rationellt. Då är x=y+(-r) rationellt eftersom summan av två rationella tal är rationell. (Q sluten under addition). Men detta strider mot förutsättningen att x var irrationellt. Bev.
Här är ett alternativ som brukar förekomma.

Hoppsan
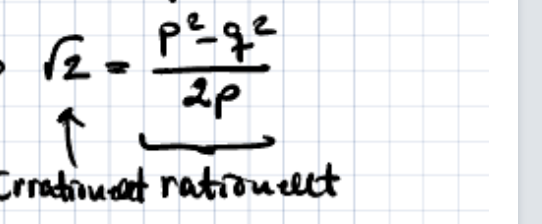
Nog ska det inte vara 2pq i nämnaren i det sista uttrycket?
Det ändrar dock inte slutsatsen
Hoppsan
Skulle stå:
Nog ska det väl vara 2pq i nämnaren i det sista uttrycket?
Arktos skrev:Hoppsan
Nog ska det inte vara 2pq i nämnaren i det sista uttrycket?
Det ändrar dock inte slutsatsen
Observant! Bra. Slarvigt av mig.
Varför blir roten ur två irrationellt i det sista uttrycket?