Två kulor som faller

Så här tolkar jag uppgiften

Du har räknat ut hur långt den första kulan har fallit när den andra släpps, men är det samma avstånd när den första har fallit 15 m?

Nu har du ju markerat uppgiften som att du inte behöver mer hjälp, men som Laguna skriver har du inte rätt svar. Du behöver använda 15 meter för att lösa problemet.

kan jag tänka mig att$s_1=s_2=15 m$

kan jag använda fomreln ${v_f}^2-{v_i}^2=2as$?

Arup skrev:

kan jag tänka mig att$s_1=s_2=15 m$

Nej, det är nog ingen bra ansats. Fundera inte så mycket på vilken formel du kan använda, utan klura på vad som händer. 

Den första kulan skall falla 15 meter. Det kommer att ta den en viss tid t₁. Du kan beräkna tiden med den formel du har.

Vi den tidpunkten t₁ har den andra kulan inte fallit lika länge, utan t₁-1 sekunder.

Hur långt har den hunnit då? Samma formel, men nu söker du sträckan.

Till sist kan du beräkna avståndet mellan dem.

kan jag uttnyttja riden som jag löste i den första ekvationen till den andra ?

Det här mitt nya försök

sictransit skrev:

Arup skrev:

kan jag tänka mig att$s_1=s_2=15 m$

Nej, det är nog ingen bra ansats. Fundera inte så mycket på vilken formel du kan använda, utan klura på vad som händer. 

Den första kulan skall falla 15 meter. Det kommer att ta den en viss tid t₁. Du kan beräkna tiden med den formel du har.

Vi den tidpunkten t₁ har den andra kulan inte fallit lika länge, utan t₁-1 sekunder.

Hur långt har den hunnit då? Samma formel, men nu söker du sträckan.

Till sist kan du beräkna avståndet mellan dem.

Visa spoiler

Jag får det till lite drygt 12 meter.

Jag förstår inte hur du menar ? Asså jag försökte göra som du sa i #9 men får bara fel

Mitt svar var #7, men det spelar mindre roll.

Kika här och fundera lite på vad du räknat ut, samt (som jag sade) vad som händer uppgiften:

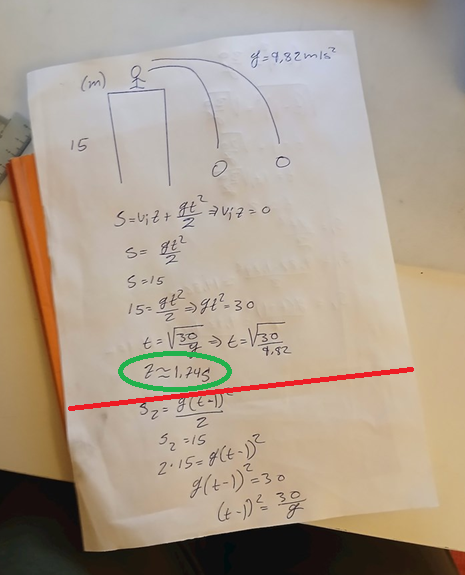
Det tar den första kulan ungefär 1,75 sekunder att falla 15 meter. Se det jag ringat in med grönt och notera att jag skriver 1,75. Avrunda korrekt om du måste avrunda.

Sedan, efter mitt röda streck, sätter du s₂=15. Varför då?

Uppgiften säger att den andra kulan släpps 1,0 sekunder efter den första, så som jag skrev i #7 borde du istället sätta t₂ till 1,75-1=0,75 sekunder. 

Du behöver räkna ut hur långt den andra kulan fallit på den tiden. När du vet hur långt båda fallit så kan du räkna ut avståndet mellan dem.

Jag ser på en av dina skisser att du kanske inte har koll på vad som händer. Så här skulle jag rita:

Kommer du vidare nu?

kan jag använda s=vt här ?

s = v*t gäller alltid. Men eftersom hastigheten v inte är konstant så blir det ändå inte så enkelt.

======

Om du har kört fast på de tidigare spåren så föreslår jag här ett annat sätt att visualisera och sedan ta sig an uppgiften.

Rita två v/t-grafer, en för kula 1 (K1) och en för kula 2 (K2). Eftersom accelerationen är konstant så blir båda v/t-graferna räta linjer.

Den tillryggalagda sträckan för kulorna är lika stor som arean under respektive graf (trianglarna).

Säg att K1 fallit 15 meter vid tidpunkten t₁.

Då är avståndet mellan de båda kulorna lika stort som skillnaden mellan areorna. Jag har markerat denna i bilden.

Kommer du vidare då?

jag försåtår vilken formel jag ska använda är det den här $s=v_{i}t+\frac{a{t}^2}{2}$

eller $s=vt$?

Jag tror nog jag föredrar Sictransit:s bild eftersom den liknar min bild i  #2 och 

hjälper visulalisera förloppet.

Arup skrev:

jag försåtår vilken formel jag ska använda är det den här $s=v_{i}t+\frac{a{t}^2}{2}$

eller $s=vt$?

 Den förstnämnda (om du med v_i menar ursprungshastigheten).

Generellt gäller för rörelse med konstant acceleration (i det här fallet, fritt fall) att positionen $s(t)=s_0+v_0t+\frac{at^2}{2}$

Om rörelsen utgår från origo så blir $s_0=0$ och man får då formeln du angav.

Om dessutom rörelsen startar från vila så blir $v_0=0$ och formeln blir då helt enkelt $s(t)=\frac{at^2}{2}$.

Som Yngve skriver är det $s=\frac{\mathrm{g}{t}^2}{2}$ du behöver använda, två gånger.

Du har redan klarat av den första, där du bestämde t₁≈1,75 sekunder. Det är tiden det tar kula #1 att falla s₁=15 meter.

Nu behöver du använda den igen för att beräkna s₂, alltså hur långt kula #2 har fallit. Den har inte fallit lika länge som kula #1, utan t₂=t₁-1 sekunder.

sictransit skrev:

Som Yngve skriver är det $s=\frac{\mathrm{g}{t}^2}{2}$ du behöver använda, två gånger.

Du har redan klarat av den första, där du bestämde t₁≈1,75 sekunder. Det är tiden det tar kula #1 att falla s₁=15 meter.

Nu behöver du använda den igen för att beräkna s₂, alltså hur långt kula #2 har fallit. Den har inte fallit lika länge som kula #1, utan t₂=t₁-1 sekunder.

Då undrar jag det röd markerade i #12 blev fel ?

Arup skrev:

Då undrar jag det röd markerade i #12 blev fel ?

Det som står under det röda strecket i #12 är fel, ja 

Du ska inte sätta s₂ till 15, du ska istället ta reda på vad s₂ är då kula 1 har fallit 15 meter, dvs då kula 1 har fallit 1,75 sekunder, dvs då kula 2 har fallit 1,75-1 = 0,75 sekunder.

Det ger dig s₂ och du kan sedan beräkna avståndet mellan kulorna med hjälp av 15-s₂

Kan man uttrycka den andra kulans falltid som t-1 sekunder ?

Arup skrev:

Kan man uttrycka den andra kulans falltid som t-1 sekunder ?

Absolut. Det är så den är definierad i uppgiften: t₂=t₁-1

Då kommer du att få en funktion s₂(t₁). 

Nu har du ju beräknat t₁ givet s₁, så du kan ta det ett steg till och få s₂(s₁). Avståndet mellan dem är då S=s₁-s₂(s₁). Se där! En funktion som ger S enbart av s₁. 

Allt detta är dock mer hjärngympa än en lösning på frågan hur långt det är mellan kulorna. Prova om du har tid och lust, så bör du kunna sätta in 15 meter och få avståndet S. 

Varför kan jag inte uttrycks den andra kulans falltid som s=v0t+g(t-1)^2/2 ?

Jag är lite osäker på vd du menar här.

s står för position, inte falltid.

s(t) = v₀t+at²/2 ger dig nämligen positionen vid tidpunkten t.

=======

För kula #2 gäller att v₀ = 0, vilket ger dig att s(t) = at²/2

Du vet att när den första kulan har fallit t₁ sekunder så har den andra kulan fallit t₁-1 sekunder.

Den andra kulans position är då s(t₁-1) = a(t₁-1)²/2.

Accelerationen är väl 9,82 m/s^2 eftersom vi är i fritt fall så då kan jag väl använda mig av tyngdaccelerationen i det här fallet g~9,82

Så S(t-1)= g(t-1)^2/2 

Eller hur?

Ja, det stämmer (om du sätter att positiv riktning är neråt).

Varför hade då sictransit rödmarkerat det i #12 ?

Under der röda strecket har du skrivit att s₂ = 15. Det stämmer inte.

(onödigt inlägg av mig)

Så, Löst!

Jag undrar bara varför den andra kulans sträcka inte också är 15 m ?

Bra löst!

Som svar på din fråga: Du släpper kulorna från tornet med 1 sek mellanrum. När den första hunnit falla 15 meter, så har den andra inte hunnit falla lika långt. Den har ju fallit 1 sek kortare tid. 

jag kikade på facit och det verkar som jag har gjort fel här:

Arup skrev:

jag kikade på facit och det verkar som jag har gjort fel här:

Uppgiften frågar ju efter en sträcka och inte en tid. Är det facit till rätt uppgift?

oj, jag kikade på fel uppgift, men i huvusak har jag gjort rätt. Vet dock ej om jag hade fått alla poäng på denna uppgift

Jag är ju inte lärare eller så, men här kommer några spontana kommentarer på din lösning. Den är ju korrekt, så bra jobbat!

Kanske kan några av mina små noteringar ändå vara till nytta. 

Gör med dem vad du vill.

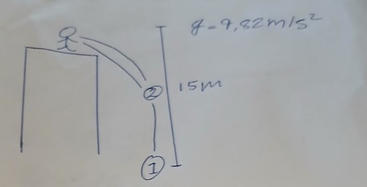
Bra med en bild! Då ser man att du förstått vad som händer.

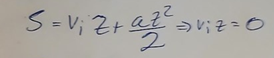
Här skulle jag ha nöjt mig med att visa att jag hittat rätt formel: s=v₀t+at²/2.

Sedan skulle jag ha skrivit något i stil med: Den initiala hastigheten v₀=0 så vi kan stryka termen. 

Jag är van att skriva text i uträkningar och det verkar som facit också förväntar sig det för A-poäng.

Typ: Kula #1 har fallit fritt i a=g=9,82 m/s² under s₁=15 meter. Vi söker tiden t₁ det tar: s₁=15=at₁²/2.

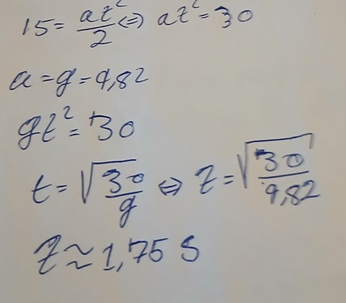
Sedan räknar du ut t1≈1,75 s, men det skadar inte att skriva ut enheter på vägen.

Du kallar dessutom tiden för t, men i nästa steg använder du t₁.

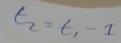
Här inför du t2, men utan kommentar. 

Kanske så här: Kula #2 släpps 1,0 s efter kula #1, så den har fallit i t₂=t₁-1,0≈0,75 s.

Här kommer ett Δt in i bilden, men det är ju inte något du använder senare. Ett Δt skulle jag spontant tycka vore 1,0 sekunder, alltså intervallet mellan kulorna släpps. Det känns inte naturligt för mig med ett Δt som är hur länge kula #2 fallit.

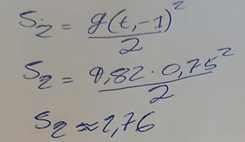
Sedan kommer uträkningen av s₂, som är alldeles korrekt. Däremot använder du inte t₂ som du nyss definierat utan istället t₁-1.

Kanske en kommentar också: Vid tiden t₂ har kula #2 fallit s₂ meter.

Till sist räknar du ut Δs, alltså avståndet mellan kulorna.  Du använder 15, men det är ju s1.

Δs=s₁-s₂ anser åtminstone jag vara lite mer konsekvent.

Svar: När kula #1 fallit 15 meter är avståndet mellan kulorna ca 12 meter.

Åter igen: Bra jobbat! Detta är bara några små synpunkter eftersom du själv ställde frågan om A-poäng.