Två lika reella rötter

Använd pq-formeln direkt på $x^2+ax+a=0$. Eftersom vi skall ha en dubbelrot skall diskriminanten vara lika med 0, d v s $\frac{a^2}{4}-a=0$. Denna andragradsekvation har lösningarna a=2 och a=-2. Alltså har funktionen en dubbelrot när a =2 eller a=-2.

EDIT: Fel, se nedan.

istället för att använda p=4 och q=4 så skall du använda p=a och q=a

diskriminanten blir då   $\frac{a^2}{4}-a$.  För vilka a är detta lika med 0?

Smaragdalena skrev:

Använd pq-formeln direkt på $x^2+ax+a=0$. Eftersom vi skall ha en dubbelrot skall diskriminanten vara lika med 0, d v s $\frac{a^2}{4}-a=0$. Denna andragradsekvation har lösningarna a=2 och a=-2. Alltså har funktionen en dubbelrot när a =2 eller a=-2.

Nja ... a=2 och a=-2 känns inte rätt. 
a=4 och a=0

Smaragdalena skrev:

Använd pq-formeln direkt på $x^2+ax+a=0$. Eftersom vi skall ha en dubbelrot skall diskriminanten vara lika med 0, d v s $\frac{a^2}{4}-a=0$. Denna andragradsekvation har lösningarna a=2 och a=-2. Alltså har funktionen en dubbelrot när a =2 eller a=-2.

Just det, jag fick också fram att jag ska ta reda på vilka värden på a som får $\frac{a^2}{4}-a=0.$ Där kan jag ju se att 0 eller 4 i stället för a gör att HL blir 0.

Men svaret ska ju enligt facit vara att ekvationen $x^2+ax+a=0$ har en dubbelrot när a = 0 och när a = 4 (inte när $a=\pm 2$).

Lisa Mårtensson skrev:

Hej!

Uppgiften jag skulle vilja ha råd kring lyder:

"För vilka värden på konstanten a har ekvationen $x^2+ax+a=0$ två lika reella rötter?"

Jag förstår att jag kan använda pq-formeln och se när det som står under rottecknet (diskriminanten) är noll. Då har jag en dubbelrot.

Jag kan även lista ut att värdena som konstanten a kan ha är 0 eller 4, eftersom sätter jag in 0 eller fyra på platsen för a i andragradsekvationen får jag 0 under rottecknet:

$$\begin{gathered} x^2+4x+4=0 p=4, q=4 \\ x=-\frac{4}{2}\pm \sqrt{{\left(\frac{4}{2}\right)}^2-4} \\ x=-2\pm \sqrt{0} \end{gathered}$$

Detta visar att för a = 4 har vi en dubbelrot vid x-värdet -2.

$x_1= -2, x_2 = -2$.

När a = 0 har vi en dubbelrot vid x-värdet 0.

Men hur visar jag detta på ett snyggt sätt?

Det svåra här tycker jag är att både p och q i pq-formeln har ersatts med a.

Jag vill ju kunna lösa ut a på ett snyggt sätt och hade lösningarna inte varit lika uppenbara så hade jag velat ha en bra metod för att lösa denna typ av uppgift.

Tar tacksamt emot råd!

Sätt p=a och q=a och använd pq-formeln som tidigare. Räkna ut den obekanta variabeln (a) som man gör med pq-formeln. Villkoret är att diskriminanten skall vara 0 och då kan du enkelt sätta upp en ekvation för att lösa problemet. Gjorde en snabb skiss men det blev inte jättetydligt så fråga gärna om det är något som är oklart.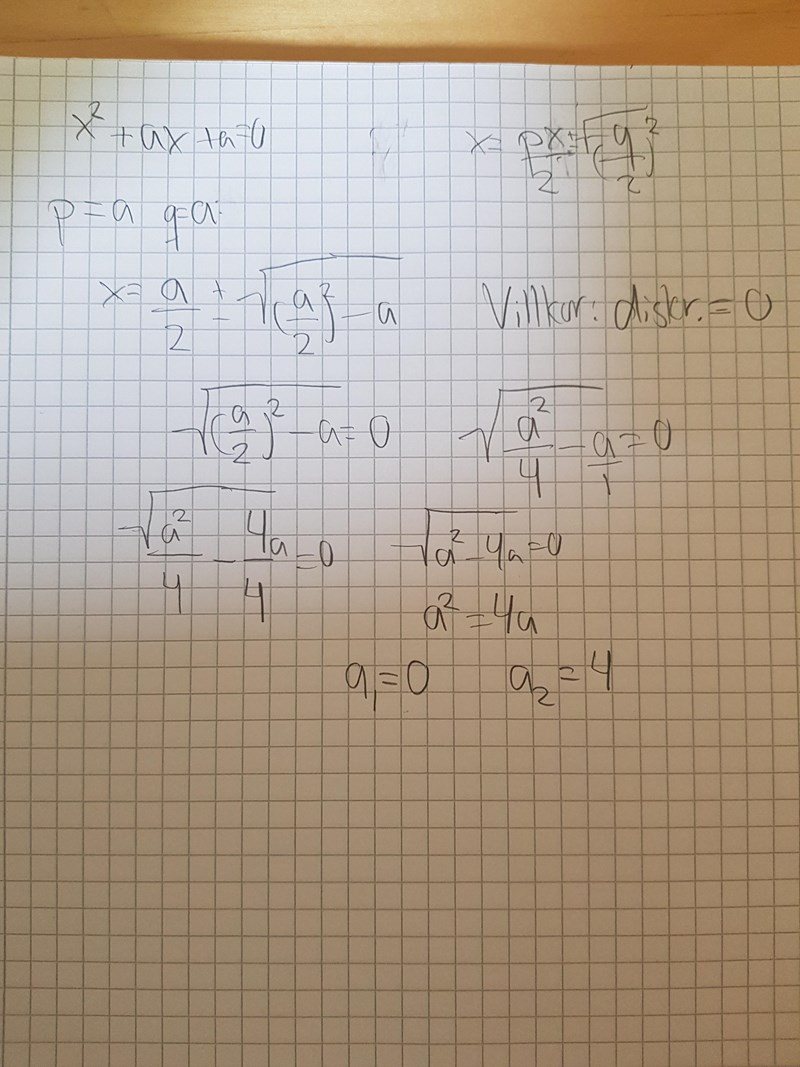

Man kan lösa andragradsekvationen $\frac{a^2}{4}-a=0$ genom att först multiplicera alla termer med 4 och sedan bryta ut a.

Då har vi att

$a^2-4a=0$ och därefter

$a(a-4)=0$.

Då¨blir det tydligt att när a = 0 eller a = 4 då är HL=0.

Jag löste andragradsekvationen på det sättet som man gör när man saknar q-värde, genom att faktorisera.

Tack alla ni som hjälpte mig.

För att jag läste din lösning och halkade in på fel spår. Ekvationen $\frac{a^2}{4}-a=0$ kan skrivas om till $a(a-4)=0$ och då ser man direkt att lösningarna är a=0 och a=4.

Smaragdalena skrev:

För att jag läste din lösning och halkade in på fel spår. Ekvationen $\frac{a^2}{4}-a=0$ kan skrivas om till $a(a-4)=0$ och då ser man direkt att lösningarna är a=0 och a=4.

Ja, Smaragdalena, jag kom på att jag hade lärt mig detta på matte 2, att lösa andragradsekvationer som saknar q-värde. Men det tog mig en stund att inse det.

Jag krånglade till det lite genom att tala om vid vilka x-värden som dubbelrötterna fanns. Det var inte det som var frågan i uppgiften.

Tack!

Hej! Låt b vara en dubbelrot till polynomet, som då kan skrivas

    $(x-b)^2=x^2-2bx+b^2$.

Identifikation med det givna polynomet ger kraven $a=b^2$ och $a=-2b$ vilket ger ekvationen $b^2+2b=0$ vars lösningar är $b=0$ och $b=-2$.