Under hur lång tid är a(t)>60 cm/s^2 (Matematik/Matte 4/Derivata)

Hej.

Du löser ekvationen y'(t) = 0, men du ska istället lösa olikheten y''(t) > 60.

Yngve skrev:
Hej.

Du löser ekvationen y'(t) = 0, men du ska istället lösa olikheten y''(t) > 60.

Men facit får t=0.549 s. Var får de ifrån?

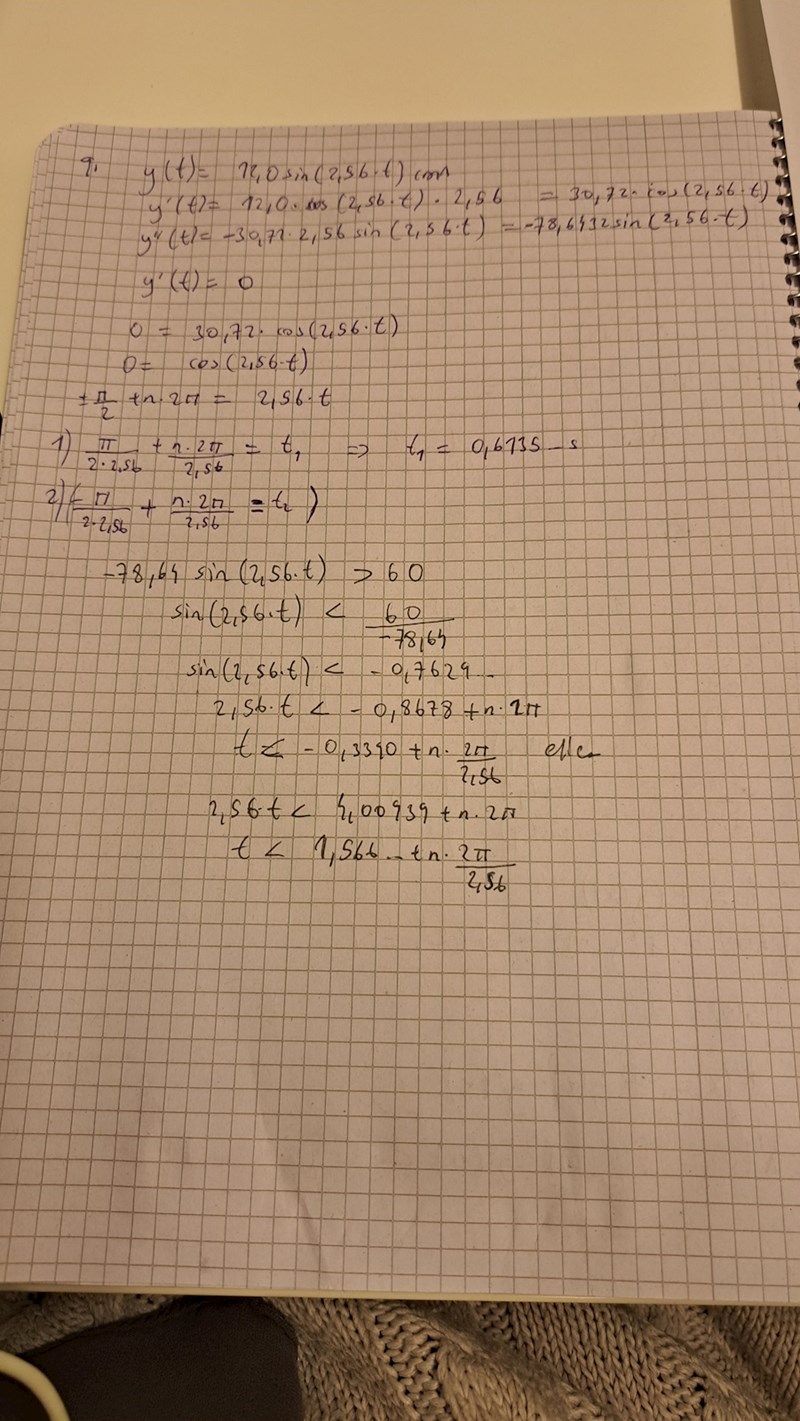
Det är rätt fram hit (översta raden).

Efter det behöver du nog använda någon illustration av olikheten sin(2,56t) < 5/2,56² för att kunna komma fram till vilka värden på t som uppfyller denna olikhet.

Använd gärna enhetscirkeln.

Yngve skrev:
Det är rätt fram hit (översta raden).

Efter det behöver du nog använda någon illustration av olikheten sin(2,56t) < 5/2,56² för att kunna komma fram till vilka värden på t som uppfyller denna olikhet.

Använd gärna enhetscirkeln.

Nu hänger jag ej med på var du får 5/2.56^2 ifrån? Jag ser ej hur vi kan använda enhetscirkeln.

Jag glömde ett minustecken, det ska vara

-5/2,56².

Det kommer från följande:

y(t) = 12*sin(2,56t)

y'(t) = 2,56*12*cos(2,56t)

y''(t) = -2,56²*12*sin(2,56t)

y''(t) > 60 ger nu -2,56²*12*sin(2,56t) > 60, vilket i sin tur ger sin(2,56t) < -5/2,56²

Det är samma resultat som du kom fram till, fast utan avrundning.

=========

Vad gäller enhetscirkeln:

Det är lurigt med olikheter där trigonometriska funktioner är inblandade. Då är enhetscirkeln ett utmärkt hjälpmedel som hjälper oss att navigera rätt.

Gör så här

Rita en enhetscirkel.
Rita en horisontell linje på höjden -5/2,56², dvs ungefär vid höjden -0,76.
Markera den del av cirkelbågen som motsvarar olikheten sin(2,56t) < -0,76.
Markera de två vinklar i intervallet [0, 2pi] som motsvarar gränsen för olikheten, dvs lösningarna till ekvationen sin(2,56t) = -5/2,56²
Visa din bild.

Yngve skrev:
Jag glömde ett minustecken, det ska vara

-5/2,56².

Det kommer från följande:

y(t) = 12*sin(2,56t)

y'(t) = 2,56*12*cos(2,56t)

y''(t) = -2,56²*12*sin(2,56t)

y''(t) > 60 ger nu -2,56²*12*sin(2,56t) > 60, vilket i sin tur ger sin(2,56t) < -5/2,56²

Det är samma resultat som du kom fram till, fast utan avrundning.

=========

Vad gäller enhetscirkeln:

Det är lurigt med olikheter där trigonometriska funktioner är inblandade. Då är enhetscirkeln ett utmärkt hjälpmedel som hjälper oss att navigera rätt.

Gör så här

Rita en enhetscirkel.

Rita en horisontell linje på höjden -5/2,56², dvs ungefär vid höjden -0,76.

Markera den del av cirkelbågen som motsvarar olikheten sin(2,56t) < -0,76.

Markera de två vinklar i intervallet [0, 2pi] som motsvarar gränsen för olikheten, dvs lösningarna till ekvationen sin(2,56t) = -5/2,56²

Visa din bild.

OK bra.

Markera nu den del av cirkelbågen som motsvarar olikheten. Det är just detta steg som hjälper dig att få fram rätt intervall för vinkeln.

Yngve skrev:
OK bra.

Markera nu den del av cirkelbågen som motsvarar olikheten. Det är just detta steg som hjälper dig att få fram rätt intervall för vinkeln.

Bra, helt rätt.

Tänk dig nu att du börjar med vinkeln 0 och ökar den tills du kommer in i det "tillåtna" området (i kvadrant 3).

Detta blir den undre gränsen för vinkeln, som vi kan kalla a. Beräkna vinkeln a vid denna gräns.

Fortsött sedan att öka vinkeln tills du lämnar det tillåtna området (i kvadrant 4).

Detta blir den övre gränsen för vinkeln, som vi kan kalla b. Beräkna vinkeln b vid denna gräns.

Olikheten är nu uppfylld för a < 2,56t < b.

Kommer du vidare då?

Yngve skrev:
Bra, helt rätt.

Tänk dig nu att du börjar med vinkeln 0 och ökar den tills du kommer in i det "tillåtna" området (i kvadrant 3).

Detta blir den undre gränsen för vinkeln, som vi kan kalla a. Beräkna vinkeln a vid denna gräns.

Fortsött sedan att öka vinkeln tills du lämnar det tillåtna området (i kvadrant 4).

Detta blir den övre gränsen för vinkeln, som vi kan kalla b. Beräkna vinkeln b vid denna gräns.

Olikheten är nu uppfylld för a < 2,56t < b.

Kommer du vidare då?

Du menar att jag ska räkna ut a=180-arcsin(-0.76) och sedan b=arcsin(-0.76)?

Ja, plus/minus lämpligt antal 2pi så att du får fram de vinklar jag har markerat som a och b i bilden:

Du ser att a bör vara mellan pi och 3pi/2 samt att b bör vara mellan 3pi/2 och 2pi.

Yngve skrev:
Ja, plus/minus lämpligt antal 2pi så att du får fram de vinklar jag har markerat som a och b i bilden:

Du ser att a bör vara mellan pi och 3pi/2 samt att b bör vara mellan 3pi/2 och 2pi.

Okej jag ser ej hur a ligger mellan pi och 3pi/2 och att b ligger mellan 3pi/2 och 2pi i figuren.

destiny99 skrev:

Okej jag ser ej hur a ligger mellan pi och 3pi/2 och att b ligger mellan 3pi/2 och 2pi i figuren.

Är du med på att vinklarna pi, 3pi/2 och 2pi är de som jag har markerat I bilden?

Yngve skrev:
destiny99 skrev:

Okej jag ser ej hur a ligger mellan pi och 3pi/2 och att b ligger mellan 3pi/2 och 2pi i figuren.

Är du med på att vinklarna pi, 3pi/2 och 2pi är de som jag har markerat I bilden?

Ja jag är med.

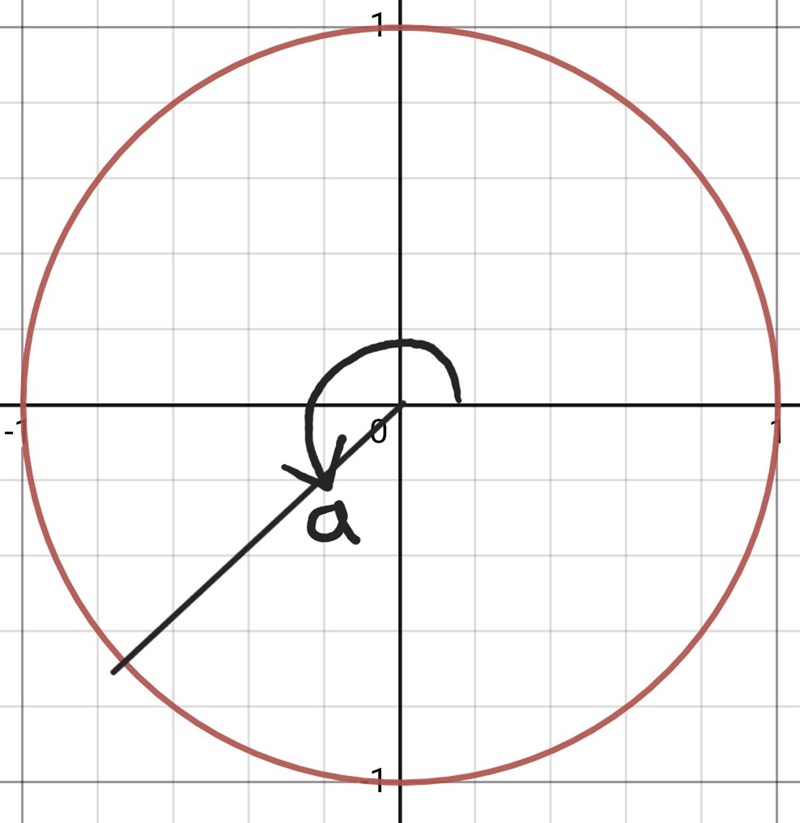
OK bra. Är du då även med på

att den vinkel jag kallar a i bilden är större än pi och mindre än 3pi/2 radianer?
att det betyder att a ligger mellan pi och 3pi/2 radianer?
att, på samma sätt, vinkeln b ligger mellan 3pi/2 och 2pi radianer?

Yngve skrev:
OK bra. Är du då även med på

att den vinkel jag kallar a i bilden är större än pi och mindre än 3pi/2 radianer?

att det betyder att a ligger mellan pi och 3pi/2 radianer?

att, på samma sätt, vinkeln b ligger mellan 3pi/2 och 2pi radianer?

Aa jag är med på det.

OK bra. Kan du då fortsätta från svar #12?

Yngve skrev:
OK bra. Kan du då fortsätta från svar #12?

a = -49.4641 grader

b= 229.46 grader

Jag tror att du blandar ihop det lite.

Vinkel a är ungefär 229°, dvs ungefär 4 radianer, se bild..

Vinkel b är ju mellan 270° och 360°, dvs mellan 3pi/2 radianer och 2pi radianer, se bild.

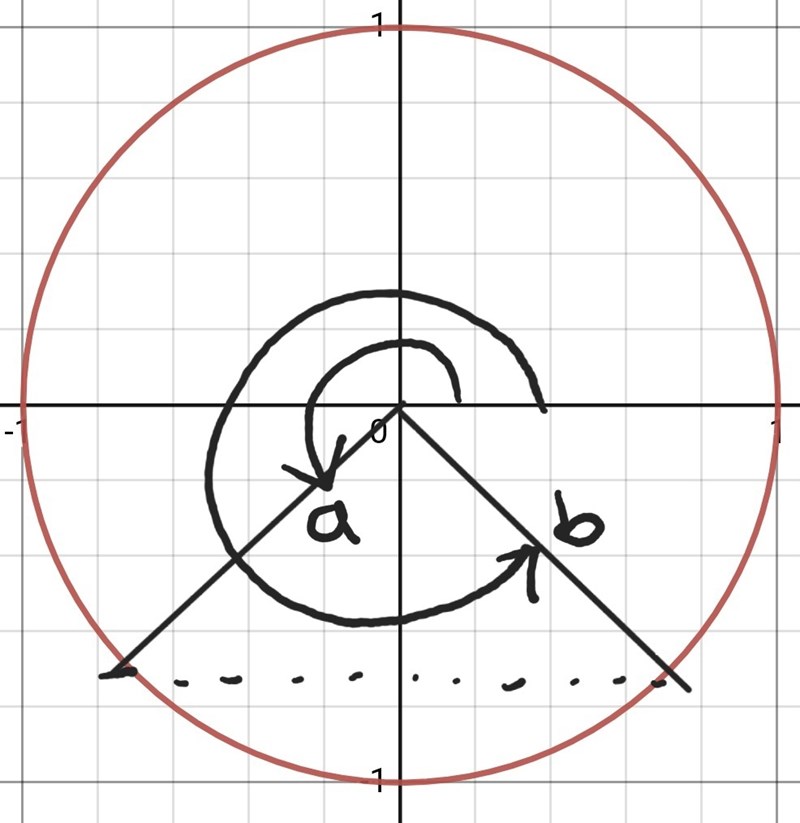
Vet du hur du ska få fram denna vinkel?

Tips: Addera ett lämpligt antal 360°/2pi radianer till en av dina lösningar.

Yngve skrev:
Jag tror att du blandar ihop det lite.

Vinkel a är ungefär 229°, dvs ungefär 4 radianer, se bild..

Vinkel b är ju mellan 270° och 360°, dvs mellan 3pi/2 radianer och 2pi radianer, se bild.

Vet du hur du ska få fram denna vinkel?

Tips: Addera ett lämpligt antal 360°/2pi radianer till en av dina lösningar.

Jag antar att man ska addera -49 grader med 360 grader för att då b? Men a är rätt eller?

destiny99 skrev:

Jag antar att man ska addera -49 grader med 360 grader för att då b?

Ja, och det är viktigt att du förstår varför det är så. Och du ska räkna i radianer

Men a är rätt eller?

Det stämner att storleken på vinkeln a är ungefär 4 radianer.

Yngve skrev:
destiny99 skrev:

Jag antar att man ska addera -49 grader med 360 grader för att då b?

Ja, och det är viktigt att du förstår varför det är så. Och du ska räkna i radianer

Men a är rätt eller?

Det stämner att storleken på vinkeln a är ungefär 4 radianer.

Eftersom vinkel b är mellan 3pi/2 och 2pi så ska man ju addera med 2pi för att komma till vinkel b. Men jag får att a= -0.8633 i radianer nu.

och b= 2pi-(-0.8633)=7.146498 radianer

destiny99 skrev:

Eftersom vinkel b är mellan 3pi/2 och 2pi så ska man ju addera med 2pi för att komma till vinkel b. Men jag får att a= -0.8633 i radianer nu.

och b= 2pi-(-0.8633)=7.146498 radianer

Visa i detalj hur du räknar ut det.

Yngve skrev:
destiny99 skrev:

Eftersom vinkel b är mellan 3pi/2 och 2pi så ska man ju addera med 2pi för att komma till vinkel b. Men jag får att a= -0.8633 i radianer nu.

och b= 2pi-(-0.8633)=7.146498 radianer

Visa i detalj hur du räknar ut det.

Jag knappade bara på räknaren arcsin(-0.76) för att få a i radianer och sedan tog jag 2pi-arcsin(-0.76) för att b i radianer. Är detta fel eller?

destiny99 skrev:

Jag knappade bara på räknaren arcsin(-0.76) för att få a i radianer och sedan tog jag 2pi-arcsin(-0.76) för att b i radianer. Är detta fel eller?

-0,86 radianer är rätt, det motsvarar -49,5°.

Om du adderar 2pi radianer till denna vinkel så får du binkel b, inte a.

Flr att få vinkel a ska du ta pi-(-0,86), inte 2pi-(-0,86).

Yngve skrev:
destiny99 skrev:

Jag knappade bara på räknaren arcsin(-0.76) för att få a i radianer och sedan tog jag 2pi-arcsin(-0.76) för att b i radianer. Är detta fel eller?

-0,86 radianer är rätt, det motsvarar -49,5°.

Om du adderar 2pi radianer till denna vinkel så får du binkel b, inte a.

Flr att få vinkel a ska du ta pi-(-0,86), inte 2pi-(-0,86).

Okej. varför skall jag ta pi-(-0.86) för att få a? Du sa precis att -0.86 radianer är rätt. Varför kan ej det värdet motsvara a ?

destiny99 skrev:
Okej. varför skall jag ta pi-(-0.86) för att få a?

Du sa precis att -0.86 radianer är rätt. Varför kan ej det värdet motsvara a ?

Vinkeln -0,86 radianer motsvarar vinkeln jag i bilden kallar c (alltså ungefär lika med -49,5°).

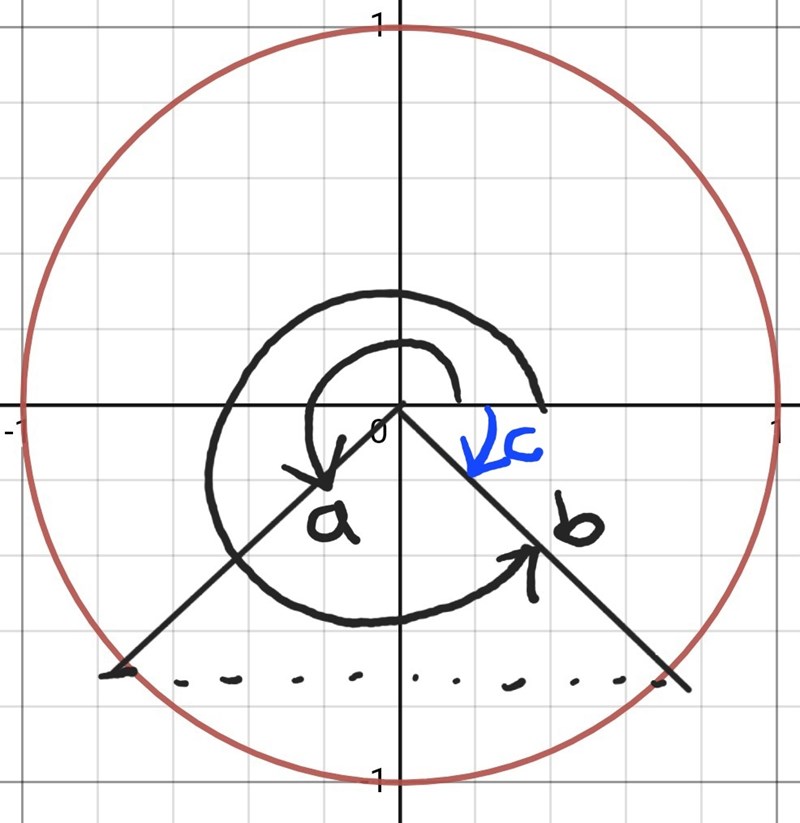
För att få vinkel a (som ligger i tredje kvadranten) så ska du ta pi-(-0,86), vilket motsvarar 180°-(-49,5°) om du räknar i grader. Detta eftersom 180° = pi radianer.

För att få vinkel b ska du ta -0,86+2pi. Se bild.

=======

Jag misdtänker att du blir förvirrad av att räkna i radianer. Släpp då det ett tag, räkna istället fram vinkel a och b i grader först och översätt först därefter dessa till radianer innan du går vidare.

Yngve skrev:
destiny99 skrev:
Okej. varför skall jag ta pi-(-0.86) för att få a?

Du sa precis att -0.86 radianer är rätt. Varför kan ej det värdet motsvara a ?

Vinkeln -0,86 radianer motsvarar vinkeln jag i bilden kallar c (alltså ungefär lika med -49,5°).

För att få vinkel a (som ligger i tredje kvadranten) så ska du ta pi-(-0,86), vilket motsvarar 180°-(-49,5°) om du räknar i grader. Detta eftersom 180° = pi radianer.

För att få vinkel b ska du ta -0,86+2pi. Se bild.

=======

Jag misdtänker att du blir förvirrad av att räkna i radianer. Släpp då det ett tag, räkna istället fram vinkel a och b i grader först och översätt först därefter dessa till radianer innan du går vidare.

Nej jag är ej förvirrad av radianer riktigt. Jag förväntade mig att vi skulle räkna på grader i denna uppgift men jag kan tänka mig radianer är bättre eller passande för uppgiften i fråga. Mha radianer får jag a till 4.00159 och b= 5.42318

OK bra, det stämmer.

Om vi ska vara noga så blir $a\approx4.009440579$ och $b\approx5.415337382$ .

Avrundat blir det $a\approx4.009$ och $b\approx5.415$ .

Kan du fortsätta därifrån?

Yngve skrev:
OK bra, det stämmer.

Om vi ska vara noga så blir $a\approx4.009440579$ och $b\approx5.415337382$ .

Avrundat blir det $a\approx4.009$ och $b\approx5.415$ .

Kan du fortsätta därifrån?

Precis jag tog ej med alla decimaler för de är för många. Tack ändå!

Vad ska jag fortsätta med ?

destiny99 skrev:

Precis jag tog ej med alla decimaler för de är för många. Tack ändå!

Vad ska jag fortsätta med ?

Bra. Du kan nu läsa svar #10 igen. Där står det hur du kan fortsätta.

Men det är viktigt att du förstår varför det som står där är nästa steg.

Yngve skrev:
destiny99 skrev:

Precis jag tog ej med alla decimaler för de är för många. Tack ändå!

Vad ska jag fortsätta med ?

Bra. Du kan nu läsa svar #10 igen. Där står det hur du kan fortsätta.

Men det är viktigt att du förstår varför det som står där är nästa steg.

Vi ska alltså ha olikheten 4.009/2.56<t<5.415/2.56

Ja, det stämmer.

Och det är hör det blir skillnad på om vi använder radianer eller grader.

Yngve skrev:
Ja, det stämmer.

Och det är hör det blir skillnad på om vi använder radianer eller grader.

Ja men nu har vi använt radianer

Japp, så det är bara att köra vidare. Du är väldigt nära svaret nu.

Yngve skrev:
Japp, så det är bara att köra vidare. Du är väldigt nära svaret nu.

Nu har jag 1.5660<t<2.11523

OK. Kan du besvara frågan då?

Yngve skrev:
OK. Kan du besvara frågan då?

Jag vet ej hur jag ska besvara frågan. Vi har fått att t ligger mellan ett intervall.

Frågan lyder "Under hur lång tid är a(t) > 60 cm/s² i varje period?"

Du har kommit fram till att olikheten gäller från t $\approx$ 1,6 s till t $\approx$ 2,1 s (i första perioden).

Hur lång tid är det?

Yngve skrev:
Frågan lyder "Under hur lång tid är a(t) > 60 cm/s² i varje period?"

Du har kommit fram till att olikheten gäller från t $\approx$ 1,6 s till t $\approx$ 2,1 s (i första perioden).

Hur lång tid är det?

0.5 s

Ja, det är svaret.

Bra att du är envis och tålmodig.

Fundera på om det är något steg i lösningen som du vill att vi förklarar mer ingående.

Yngve skrev:
Ja, det är svaret.

Bra att du är envis och tålmodig.

Fundera på om det är något steg i lösningen som du vill att vi förklarar mer ingående.

Ok tack ändå!