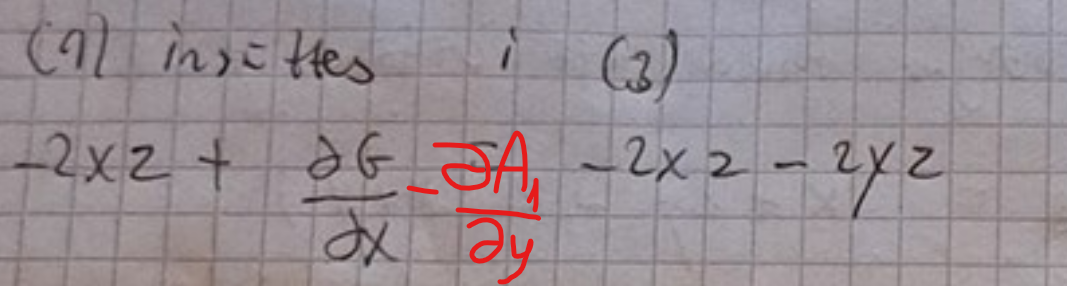Undersök om B har vektorpotential och bestämma den så den är vinkelrät mot ez

Genom att beräkna div B och få 0 visar du att vektorfältet B verkligen har en vektorpotential (Sats 7.7).

För att sedan hitta vektorpotentialen A, så utgår man från vektorpotentialens definition (7.19), d.v.s. rot A = B.

Man söker alltså vektorfältet $\mathbf{A}\left(x,y,z\right) = \begin{pmatrix} A_1(x,y,z) \\ A_2(x,y,z) \\ A_3(x,y,z)\end{pmatrix}$ som är vinkelrät mot vektorn $\mathbf{e}_z = \begin{pmatrix}0\\0\\1\end{pmatrix}$.

Skalärprodukten mellan A och e_z ska således vara 0. I synnerhet är $A_3(x,y,z)=0$. Det återstår att hitta $A_1(x,y,z)$ och $A_2(x,y,z)$. Teckna rot A och lös ut $A_1$ och $A_2$ ur differentialekvationssystemet rot A = B.

LuMa07 skrev:

Genom att beräkna div B och få 0 visar du att vektorfältet B verkligen har en vektorpotential (Sats 7.7).

För att sedan hitta vektorpotentialen A, så utgår man från vektorpotentialens definition (7.19), d.v.s. rot A = B.

Man söker alltså vektorfältet $\mathbf{A}\left(x,y,z\right) = \begin{pmatrix} A_1(x,y,z) \\ A_2(x,y,z) \\ A_3(x,y,z)\end{pmatrix}$ som är vinkelrät mot vektorn $\mathbf{e}_z = \begin{pmatrix}0\\0\\1\end{pmatrix}$.

Skalärprodukten mellan A och e_z ska således vara 0. I synnerhet är $A_3(x,y,z)=0$. Det återstår att hitta $A_1(x,y,z)$ och $A_2(x,y,z)$. Teckna rot A och lös ut $A_1$ och $A_2$ ur differentialekvationssystemet rot A = B.

Hm jag är med på att undersöka om B har en vektorpotential enligt satsen. Men jag är osäker på om jag ska först utföra rotA och sätta lika med B som första steg och sen sätta A3 =1 pga skalärprodukten då A och ez ska vara ortgonala. 

Om skalärprodukten mellan A och e_z skall vara noll, så måste $A_3$ vara noll (d.v.s. inte 1).

Den sökta potentialen A uppfyller rot A = B, där

$\mathrm{rot}\,\mathbf{A}=\mathrm{rot}\,\begin{pmatrix}A_1\\A_2\\0\end{pmatrix} = \begin{pmatrix}-\partial A_2/\partial z \\ \partial A_1/\partial z \\ \partial A_2/\partial x - \partial A_1/\partial y \end{pmatrix}$

och detta skall vara lika med $\mathbf{B} = \begin{pmatrix}x^2 \\ y^2 \\ -2xz - 2yz\end{pmatrix}$

LuMa07 skrev:

Om skalärprodukten mellan A och e_z skall vara noll, så måste $A_3$ vara noll (d.v.s. inte 1).

 

Den sökta potentialen A uppfyller rot A = B, där

$\mathrm{rot}\,\mathbf{A}=\mathrm{rot}\,\begin{pmatrix}A_1\\A_2\\0\end{pmatrix} = \begin{pmatrix}-\partial A_2/\partial z \\ \partial A_1/\partial z \\ \partial A_2/\partial x - \partial A_1/\partial y \end{pmatrix}$

och detta skall vara lika med $\mathbf{B} = \begin{pmatrix}x^2 \\ y^2 \\ -2xz - 2yz\end{pmatrix}$

Ja okej. Jag får detta till slut som svar på vad vektorpotential A blir.

Följande steg är inte korrekt då $A_1$ ännu inte tagits fram och termen $\partial A_1/\partial y$ får inte bara försvinna i ekvationen (3):

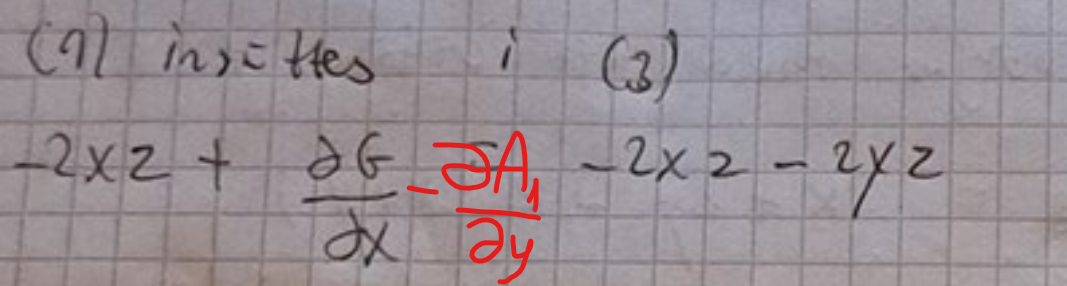
Från (1) tar man fram $A_2$. (Det har du gjort)

Från (2) tar man fram $A_1$. (Det har du inte gjort)

DÄREFTER sätts både $A_1$ och $A_2$ in i (3)

LuMa07 skrev:

Följande steg är inte korrekt då $A_1$ ännu inte tagits fram och termen $\partial A_1/\partial y$ får inte bara försvinna i ekvationen (3):

 

Från (1) tar man fram $A_2$. (Det har du gjort)

Från (2) tar man fram $A_1$. (Det har du inte gjort)

DÄREFTER sätts både $A_1$ och $A_2$ in i (3)

Ah ok. Ja jag kan tänka mig det blir dG/dx-dA1/dy=-2yz=> 

G(x)=-2xyz+A₁(x,y,z)+F(y). Vad gör man i nästa steg ?

Vad är ditt $A_1$ som du beräknat m.h.a. ekvationen (2): $\dfrac{\partial A_1}{\partial z} = y^2$?

Sätt in det i (3).

LuMa07 skrev:

Vad är ditt $A_1$ som du beräknat m.h.a. ekvationen (2): $\dfrac{\partial A_1}{\partial z} = y^2$?

Sätt in det i (3).

Det här är vad jag har nu. Se bild nedan.

Resten suddade jag för de var felaktiga som jag förstod. 

Det stämmer ju inte att integralen av $\frac{\partial A_1}{\partial y}$ med avseende på $x$ skulle ge $A_1$.

Du har korrekt kommit fram till att

$A_2=-x^2z+G(x,y)$

För att inte krångla till det är det bättre om du fortsätter lösa ett liknande uttryck för $A_1$ genom din andra ekvation

$\displaystyle \frac{\partial A_1}{\partial z}=y^2$

Slutligen sätter du in uttrycken för $A_1$ och $A_2$ i din sista ekvation, då får du ett samband mellan konstantfunktionerna. Det är också värt att lägga märke till att uppgiften söker "en" potentialfunktion, du behöver alltså egentligen inte ta fram en allmän lösning, även om det är en bra övning.

D4NIEL skrev:

Det stämmer ju inte att integralen av $\frac{\partial A_1}{\partial y}$ med avseende på $x$ skulle ge $A_1$.

Du har korrekt kommit fram till att

$A_2=-x^2z+G(x,y)$

För att inte krångla till det är det bättre om du fortsätter lösa ett liknande uttryck för $A_1$ genom din andra ekvation

$\displaystyle \frac{\partial A_1}{\partial z}=y^2$

Slutligen sätter du in uttrycken för $A_1$ och $A_2$ i din sista ekvation, då får du ett samband mellan konstantfunktionerna. Det är också värt att lägga märke till att uppgiften söker "en" potentialfunktion, du behöver alltså egentligen inte ta fram en allmän lösning, även om det är en bra övning.

Ja okej jag vet inte i vilket steg jag ska börja med för att fortsätta med (2) eller hur du menar att man ska göra där?

Justnu har jag detta. Men jag antar att jag ska ta bort eller återkomma till den?

Din andra ekvation säger att 

$\displaystyle \frac{\partial A_1}{\partial z}=y^2 \implies A_1=y^2z+H\left(x,y\right)$

Nu har du uttryck för $A_1$ och $A_2$, därmed kan du ställa upp ekvation 3 och finna ett samband mellan dina okända konstantfunktioner $G(x,y)$ och $H(x,y)$.

D4NIEL skrev:

Din andra ekvation säger att 

$\displaystyle \frac{\partial A_1}{\partial z}=y^2 \implies A_1=y^2z+H\left(x,y\right)$

Nu har du uttryck för $A_1$ och $A_2$, därmed kan du ställa upp ekvation 3 och finna ett samband mellan dina okända konstantfunktioner $G(x,y)$ och $H(x,y)$.

Ja precis jag har nu uttryck för A1 och A2. Men ska jag derivera dem för att sätta in ekvation 3) ? Jag förstår inte vad du menar med att ställa upp ekvation 3.

Ja, din tredje ekvation säger ju att

$\displaystyle \frac{\partial A_2}{\partial x}-\frac{\partial A_1}{\partial y} =-2xz-2yz$

Det ger ett samband mellan $H(x,y)$ och $G(x,y)$. 

D4NIEL skrev:

Ja, din tredje ekvation säger ju att

$\displaystyle \frac{\partial A_2}{\partial x}-\frac{\partial A_1}{\partial y} =-2xz-2yz$

Det ger ett samband mellan $H(x,y)$ och $G(x,y)$. 

Ja jag får detta system och samband. Hur går jag vidare sen?

Jag tror det har blivit slarvfel i räkningarna.

$A_1=y^2z+h(x,y)$

$A_2=-x^2z+g(x,y)$

Ekvation 3, dvs 

$\frac{\partial A_2}{\partial x}-\frac{\partial A_1}{\partial y}=-2(x+y)z$

Förenklas till

$\frac{\partial g(x,y)}{\partial x}-\frac{\partial h(x,y)}{\partial y}=0$

D4NIEL skrev:

Jag tror det har blivit slarvfel i räkningarna.

$A_1=y^2z+h(x,y)$

$A_2=-x^2z+g(x,y)$

Ekvation 3, dvs 

$\frac{\partial A_2}{\partial x}-\frac{\partial A_1}{\partial y}=-2(x+y)z$

Förenklas till

$\frac{\partial g(x,y)}{\partial x}-\frac{\partial h(x,y)}{\partial y}=0$

 Såhär får jag nu. Hur ska vi hitta funktionerna h och g?

Blir potentialfunktionen bara phi(x,y,z)=A₁+A₂ ? Jag vet inte hur vi ska hantera h och g när differensen av deras partiella derivator map på x och y blir 0. 

Det du gör nu är kanske överkurs.

Vektorpotentialen till ett vektorfält är aldrig entydigt bestämd av $\nabla \times \mathbf{A}=\mathbf{B}$ eftersom vi alltid kan ansätta gradienten av en skalär funktion $\psi$ så här:

$\mathbf{A}\to \mathbf{A}^\prime=A+\nabla \psi$ (1)

Nu uppfyller detta nya fält också grundekvationen eftersom

$\nabla \times (\mathbf{A}+\nabla \psi)=\nabla \times \mathbf{A}+\nabla \times (\nabla \psi)=\nabla \times  \mathbf{A}$

En ändring av vektorpotentialen enligt (1) kallas gaugetransformation. Jämför med hur den "vanliga" potentialen endast kan bestämmas på en konstant när.

Från ekvationen $\nabla \times \mathbf{A}=\mathbf{B}$ kan vi alltså inte förvänta oss ett entydigt fält. Med det extra villkoret $A_3=0$ förenklas gaugevillkoret till det klassiska villkoret för blandade partialderivator i två dimensioner.

Om du sätter $h=\psi_x,\quad g=\psi_y$ är villkoret $\partial_x g=\partial_y h$ ett (lokalt) nödvändigt och tillräckligt villkor för att fullständigt skapa potentialfunktionen $\psi$.

Du har löst uppgiften och kommit fram till att

$\mathbf{A}=(y^2z+\psi_x, -x^2z+\psi_y,0)$

Om du vill kan du sätta $\psi=0$. Då har du hittat _en_  vektorpotential $\mathbf{A}$ vilket är vad uppgiften kräver om du läser uppgiftsformuleringen noga. 

Om du vill krångla till det kan du t.ex. definiera det skalära fältet $\psi\left(x,y\right)=\frac13x^3y-\cos\left(y\right)$ som uppfyller villkoret för de blandade derivatorna och därmed är 

$\mathbf{A}=(y^2z+x^2y, -x^2z+\frac13x^3+\sin\left(y\right),0)$

också en vektorpotential. Så länge din skalära funktion $\psi$ uppfyller villkoret som du tagit fram för $g$ och $h$ kan du alltså skapa oändligt många olika vektorpotentialer $\mathbf{A}$.

D4NIEL skrev:

Det du gör nu är kanske överkurs.

Vektorpotentialen till ett vektorfält är aldrig entydigt bestämd av $\nabla \times \mathbf{A}=\mathbf{B}$ eftersom vi alltid kan ansätta gradienten av en skalär funktion $\psi$ så här:

$\mathbf{A}\to \mathbf{A}^\prime=A+\nabla \psi$ (1)

Nu uppfyller detta nya fält också grundekvationen eftersom

$\nabla \times (\mathbf{A}+\nabla \psi)=\nabla \times \mathbf{A}+\nabla \times (\nabla \psi)=\nabla \times  \mathbf{A}$

En ändring av vektorpotentialen enligt (1) kallas gaugetransformation. Jämför med hur den "vanliga" potentialen endast kan bestämmas på en konstant när.

Från ekvationen $\nabla \times \mathbf{A}=\mathbf{B}$ kan vi alltså inte förvänta oss ett entydigt fält. Med det extra villkoret $A_3=0$ förenklas gaugevillkoret till det klassiska villkoret för blandade partialderivator i två dimensioner.

Om du sätter $h=\psi_x,\quad g=\psi_y$ är villkoret $\partial_x g=\partial_y h$ ett (lokalt) nödvändigt och tillräckligt villkor för att fullständigt skapa potentialfunktionen $\psi$.

Du har löst uppgiften och kommit fram till att

$\mathbf{A}=(y^2z+\psi_x, -x^2z+\psi_y,0)$

Om du vill kan du sätta $\psi=0$. Då har du hittat _en_  vektorpotential $\mathbf{A}$ vilket är vad uppgiften kräver om du läser uppgiftsformuleringen noga. 

Om du vill krångla till det kan du t.ex. definiera det skalära fältet $\psi\left(x,y\right)=\frac13x^3y-\cos\left(y\right)$ som uppfyller villkoret för de blandade derivatorna och därmed är 

$\mathbf{A}=(y^2z+x^2y, -x^2z+\frac13x^3+\sin\left(y\right),0)$

också en vektorpotential. Så länge din skalära funktion $\psi$ uppfyller villkoret som du tagit fram för $g$ och $h$ kan du alltså skapa oändligt många olika vektorpotentialer $\mathbf{A}$.

Jag tänker det kanske bara räcker att säga att det finns oändligt många vektorpotentialer och det finns bara denna vektorpotential A=(y^2z+g(x,y),-xz^2+h(x,y),0).

Ja, men tänk på att villkoret och ordningen måste specificeras, annars passar inte funktionerna ihop. Som du räknat blir det omvänd ordning, dvs

$A=(y^2z+h\left(x,y\right), -xz^2+g\left(x,y\right),0)$

med villkoret $\partial_xg-\partial_yh=0$