Undersök om man kan bestämma talet a

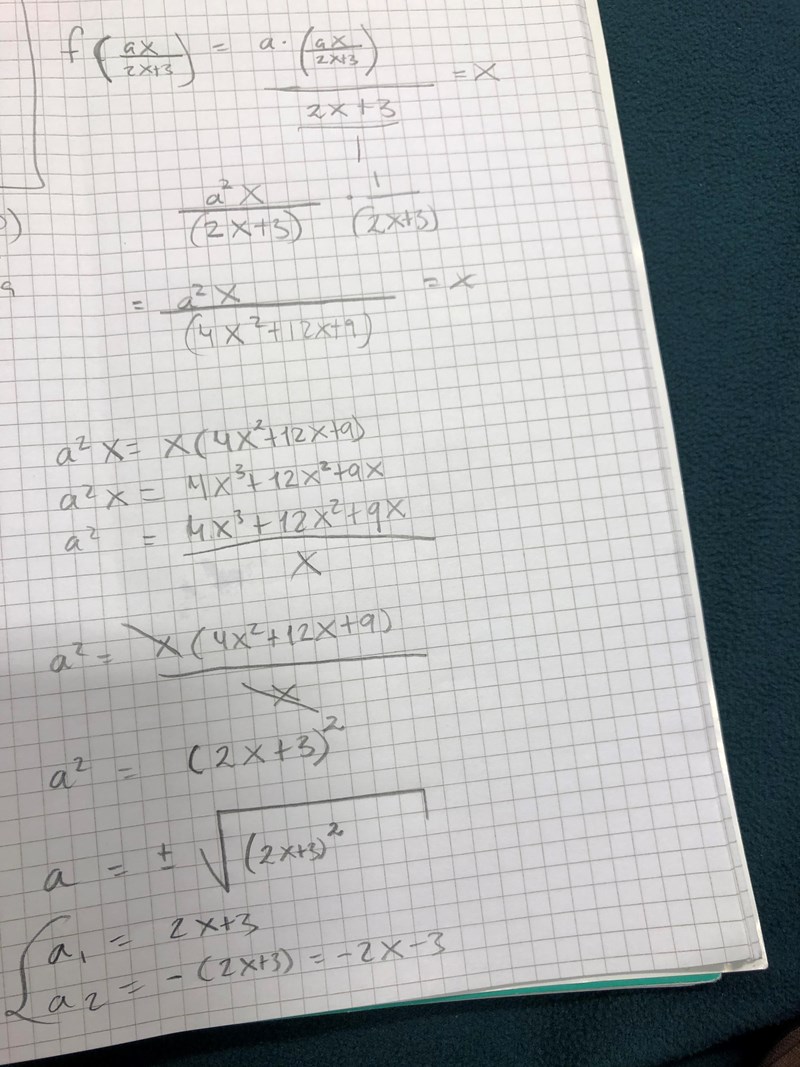 Har jag tänkt rätt?
Har jag tänkt rätt?
Nej, det ser ut som om du inte har satt in att i nämnaren, bara i täljaren.
Jag tycker att du gör rätt hela vägen, men då du drar roten ur uttrycken så bör du pröva båda lösningarna och finner då att endast den ena stämmer. Vilken?
Är det rätt nu? :
 Edit. Såg nyss att jag hade glömt lägga ”+3” i nämnaren.. Så långt har jag kommit i min nya uträkning
Edit. Såg nyss att jag hade glömt lägga ”+3” i nämnaren.. Så långt har jag kommit i min nya uträkning
 Hur kommer jag vidare?
Hur kommer jag vidare?
Det är mer rätt nu, men du har glömt termen +3 i nämnaren i första ledet
Se min nya uträkning ovan
Rätt så långt. Detta bråk ska ju sättas lika med x.
Då får du en 2-gradsekvation i a att lösa
Det blev lite krångligt här mot slutet.

Då du får fram 2-gradsekvationen i a och skriver den på normalform blir det:
Den kan du lösa med pq-formeln - lite krångligt men nyttig övning.
De två rötter du får bör du pröva - kanske är bara en rot riktig
Hur kan jag lösa en sån andragradsekvation?
är det ”-2a” som jag ska istället för p och (-6x-9) istället för q?
Ja, precis
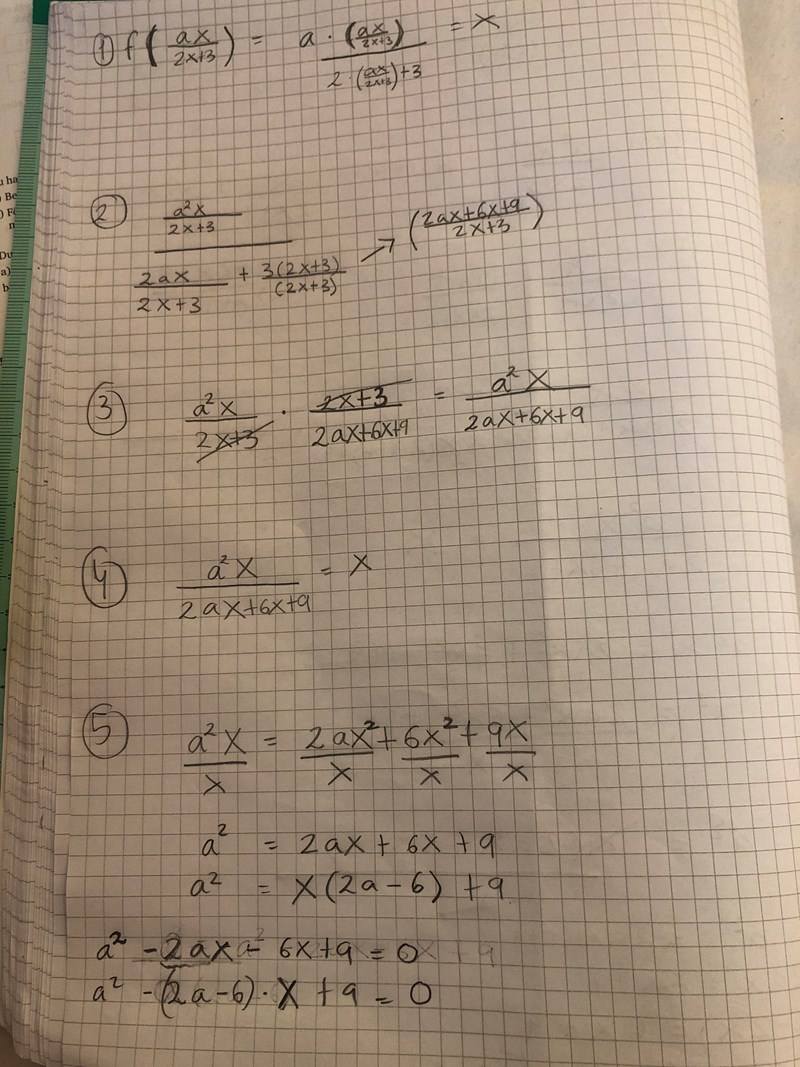
 Så löser jag den
Så löser jag den
Nja, det är lätt att blanda ihop a- och x-termerna.
Du har ekvationen:
pq-formeln ger:
Hur utvecklar du vidare?
Jag får två värden på a. 
 Eftersom att de i frågan skriver bestäm ”talet” och inte ”uttrycket” så borde a vara -3
Eftersom att de i frågan skriver bestäm ”talet” och inte ”uttrycket” så borde a vara -3
Henning skrev:Nja, det är lätt att blanda ihop a- och x-termerna.
Du har ekvationen:
pq-formeln ger:
Hur utvecklar du vidare?
Som du ser i min lösning ovan så är det x som är konstant i denna uträkning och inte a.
Så du får:
Uttrycket under rottecknet kan du skriva om med kvadreringsregeln 'baklänges' så att det blir:
Då får du: samt
Dessa två rötter bör du pröva genom att sätta in i ursprungsuttrycket
Det här som du har kommit fram till är korrekt:
a2x = 2ax2 + 6x2 + 9x
Men sedan händer konstiga saker. Vi söker ett a så att den där ekvationen är sann för alla x. Då måste x2-termerna vara lika och x-termerna vara lika. Dvs. a2 = 9 och 2a+6 = 0.
På något sätt kommer du fram till rätt värde på a, men jag tycker det verkar vara en slump.
Det känns som att jag bara blandar ihop a och x. Hur ska man kunna avgöra vad som är konstant och vad som inte är det?
Henning skrev:Henning skrev:Nja, det är lätt att blanda ihop a- och x-termerna.
Du har ekvationen:
pq-formeln ger:
Hur utvecklar du vidare?
Som du ser i min lösning ovan så är det x som är konstant i denna uträkning och inte a.
Så du får:
Uttrycket under rottecknet kan du skriva om med kvadreringsregeln 'baklänges' så att det blir:
Då får du: samt
Dessa två rötter bör du pröva genom att sätta in i oursprungsuttrycket
Nytt försök
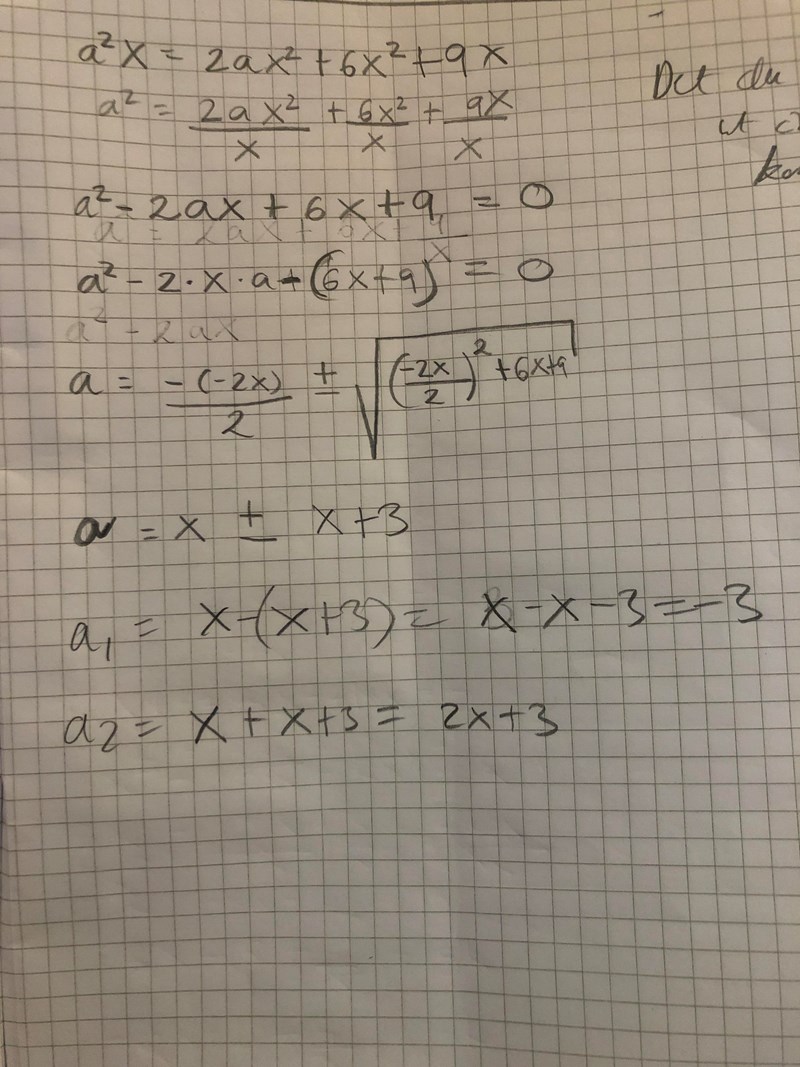
Ja, det här som du gjort senast tycker jag är rätt.
Och prövar du detta i utgångsuttrycket så stämmer båda rötterna.
Denna uppgift är verkligen inte lätt.
Är det en Ma2-uppgift?
Oavsett, så ger den matteträning på en mängd olika sätt
Bra jobbat !
solskenet skrev:Det känns som att jag bara blandar ihop a och x. Hur ska man kunna avgöra vad som är konstant och vad som inte är det?
I denna uppgift är man ute efter värden på a oberoende av x och då blir det a som är variabel.
Men verkligen inte lätt att hålla isär, särskilt då vanligen x är variabeln.
Det är därför jag undrar vilken nivå denna uppgift är placerad på
Tror att det ligger på en ma2c till 3c nivå (osäker på det iaf)
Alternativ lösning medelst invers.
...
Applicera inversen i VL & HL:
...




