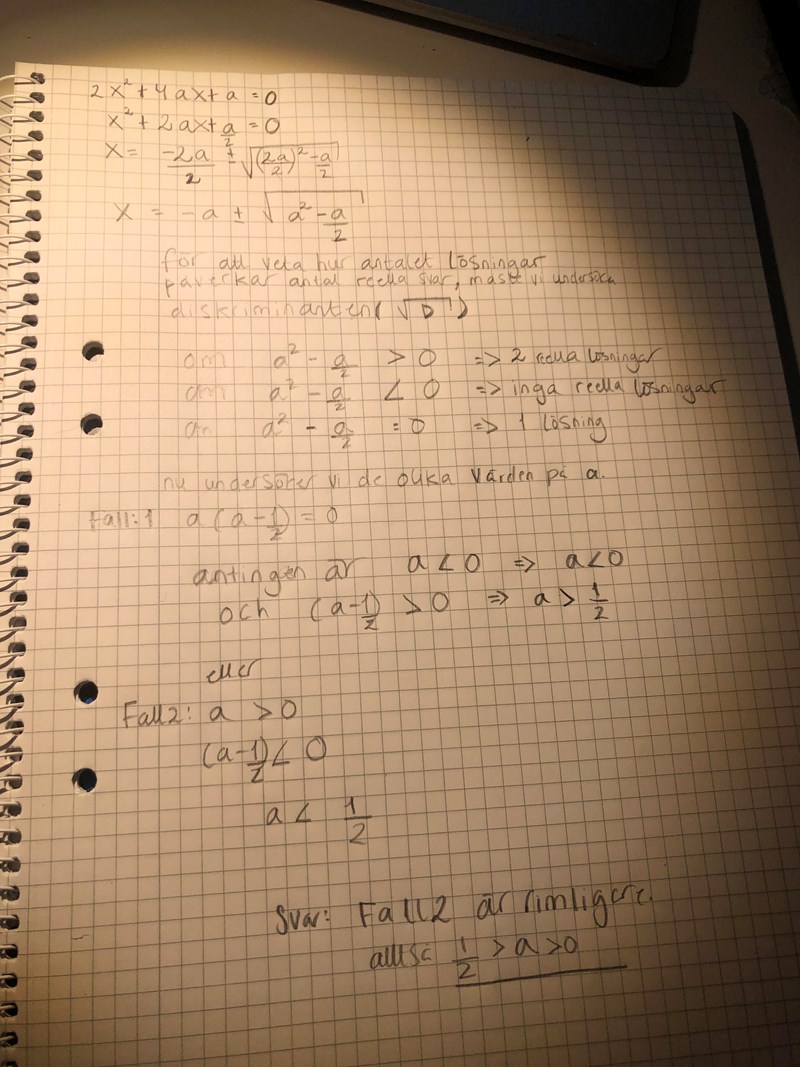Undersök värdet på a (Matematik/Matte 2/Algebra)

$2 x^{2} + 4 a x + a = 0 . D e l a m a l l t m e d 2 (p g a 2 x^{2}, m a n v i l l h a x^{2} - t e r m e n f r i) g e r o s s : x^{2} + 2 a x + \frac{a}{2} = 0 S e d a n a n v ä n d e r d u p q - f o r m e l : x = \frac{- 2 a x}{2} \pm \sqrt{{(\frac{- 2 a x}{2})}^{2} - \frac{a}{2}} \leftrightarrow - a x \pm \sqrt{{(- a x)}^{2} - \frac{a}{2}}$

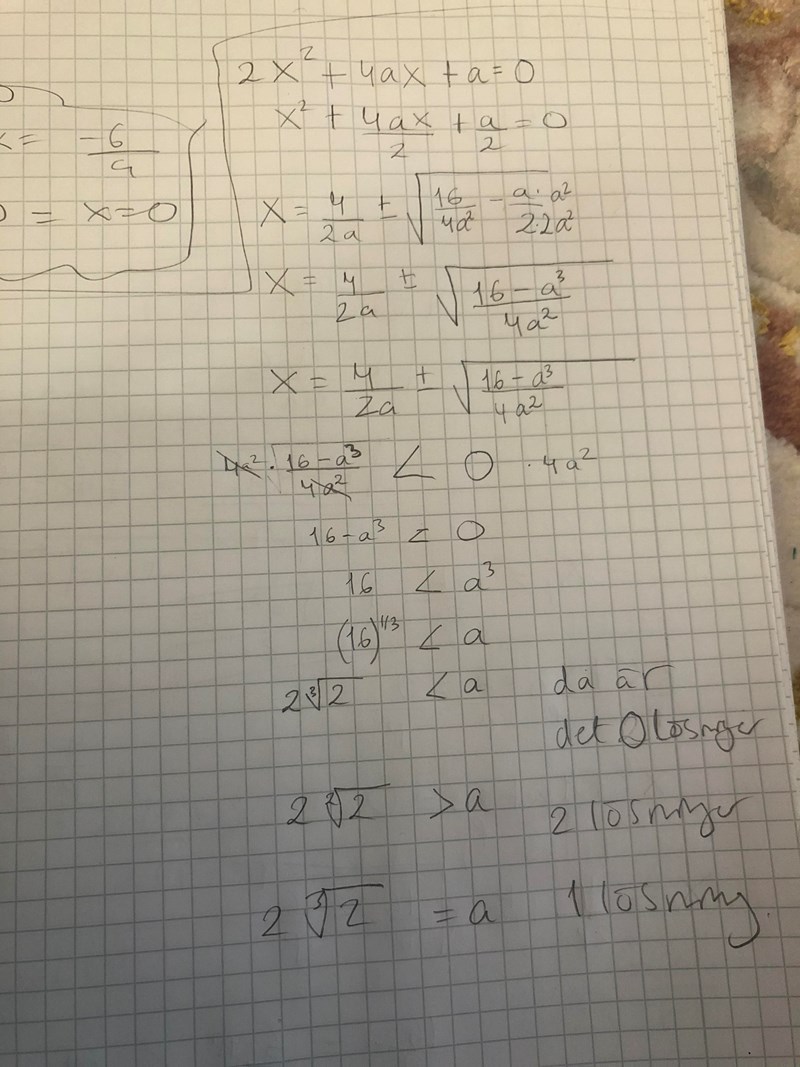
Kan du lösa uppgiften efter detta?

Har jag löst uppgiften fel?

I det första rotuttrycket har du multiplicerat täljaren med a² men nämnaren med 2a². Därifrån är det fel.

questionable 1 har använt pq-formeln fel, det skall inte vara några x i uttrycket för x.

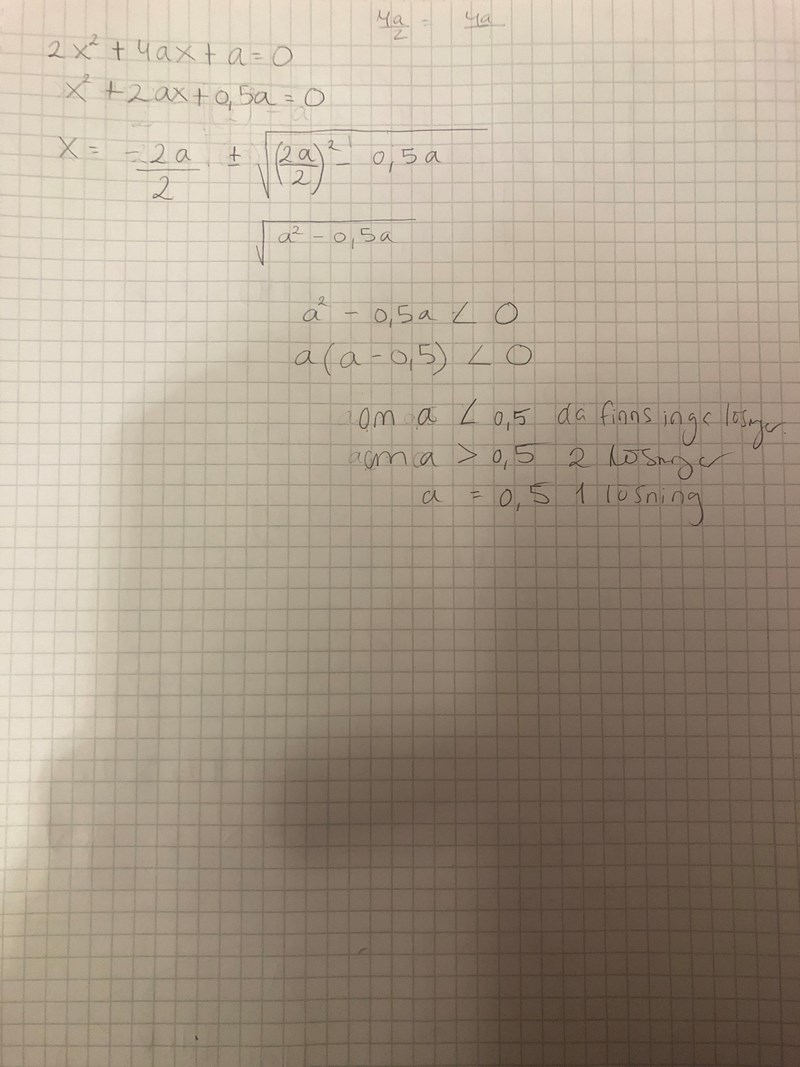Är det rätt

Nej det stämmer inte riktigt. Om a(a-0,5)<0 så måste den ena faktorn vara positiv och den andra negativ. fDu måste undersöka alla kombinationer.

Det kan finnas 2 olika fall på a

om a1=0,5 då blir uttrycket 0

om a=0 då blir uttrycket oxå noll

Du behöver motivera mer utförligt.

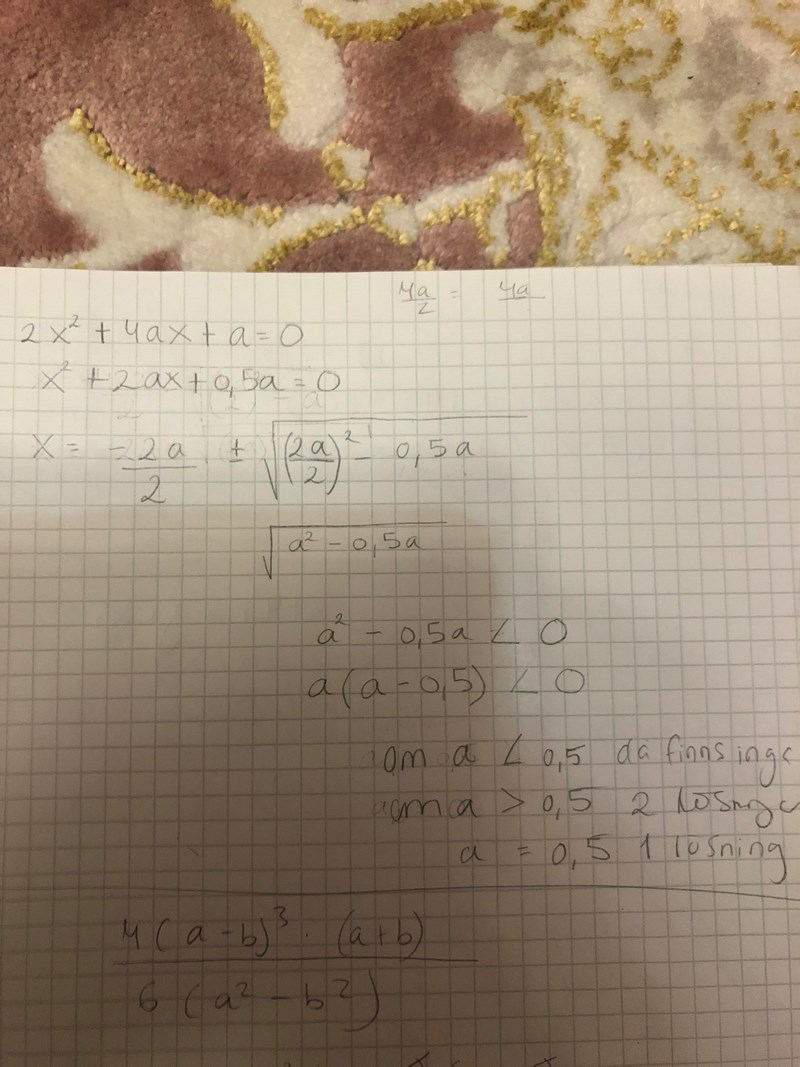Så skrev jag.

Du har redan visat den bilden och fått kommentarer.

Vad gäller för t.ex. a = -1?

Det ska stå

att om

a< 0,5 då kmr det finns 2 lösningar

om a>0,5 då finns 0 lösningar

om a=0,5 då finns 1 lösning

solskenet skrev:
Det ska stå
att om
a< 0,5 då kmr det finns 2 lösningar
om a>0,5 då finns 0 lösningar
om a=0,5 då finns 1 lösning

Det har du skrivit tidigare, och det är fortfarande inte fullständigt. Det finns t ex 2 olika värden på a som ger en dubbelrot.

Jag förstår inte hur jag ska komma fram till det svaret. Kan du hjälpa?

När är a(a-0,5) = 0?

Om a är noll och när a är 0,5

solskenet skrev:
Om a är noll och när a är 0,5

Så det finns tre intressanta intervall för att studera tecknet på a(a-0,5), nämligen:
a < 0
0 < a < 0,5 och
a > 0,5

När är a(a-0,5) < 0?

När a> 0,5

solskenet skrev:
När a> 0,5

Har du provat?

oj Det ska stå tvärtom när a<0,5 . Jag blandade ihop. Om a är tex 0,4 då kmr

0,4(0,4-0,5)=0,4*-0,1=-0,04 vilket är < 0,5

Vilket tecken (positivt eller negativt) har uttrycket a(a-½) i intervallet

a>½
0<a<½
a<0

???

Jag tror att du menar vilket tecken uttrycket a(a-0,5a) har..

Om a > 0,5 då är det + tecken

om a< 0,5 då är det - tecken

om a < 0 då är det - tecken

solskenet skrev:
Jag tror att du menar vilket tecken uttrycket a(a-0,5a) har..
Om a > 0,5 då är det + tecken
om a< 0,5 då är det - tecken
om a < 0 då är det - tecken

Nej, jag menar det jag skriver, alltså a^2-0,5a

Jag bryter ut a från uttrycket a^2 -0,5a

det blir a(a-0,5)

”vad händer om a är större än 1/2”? Svar : uttrycket får ett positivt värde alltså + tecken

vad händer om a är större än 0 men mindre än 0,5 då blir uttrycket negativt

om a är mindre än 0 uttrycket blir positivt (+ tecken)

Just det. Vad betyder det för antalet reella lösningar till ekvationen i uppgiften?

Om det är negativt finns inga reella lösningar och diskriminanten blir 0 så finns 1 lösningar. 2 lösningar finns om svaret underroteckenet blir större än 0

Just det. Vad betyder det för antalet reella lösningar till ekvationen i uppgiften?

Alltså

Om a > 0,5 då är det + tecken

om a< 0,5 då är det - tecken

om a < 0 då är det - tecken

Vilket betyderagg det endast finns reella lösningar då a> 0,5

Är det rätt tänkt?

Nej det är inte rätt.

Lösningsförslag. Läs, förstå och försök att göra på liknande sätt i dina egna lösningar framöver, dvs skriv förklarande text och skriv lösningen steg för steg.

Ekvationen är $2x^2+4ax+a=0$

Dividera båda sidor med 2:

$x^2+2ax+\frac{a}{2}=0$

Pq-formeln ger oss lösningarna

$x=-a\pm\sqrt{D}$ , där diskriminanten $D=a^2-\frac{a}{2}=a(a-\frac{1}{2})$

Vi vet att vi har

två reella lösningar då $D>0$
en reell lösning (dubbelrot) då $D=0$
inga reella lösningar då $D<0$

Frågan gäller hur värdet på $a$ påverkar antalet reella lösningar.

-------------------------------------------

Vi undersöker först fallet två reella lösningar, dvs $D>0$

Då gäller att $a(a-\frac{1}{2})>0$

För att en produkt av två faktorer ska vara större än 0 måste det gälla att båda faktorerna har samma tecken, dvs antingen är båda faktorerna mindre än 0 eller så är båda faktorerna större än 0.

Att båda faktorerna är mindre än 0 ger villkoren $a<0$ och $a-\frac{1}{2}<0$ , dvs $a<0$ och $a<\frac{1}{2}$ , dvs $a<0$

Att båda faktorerna är större än 0 ger villkoren $a>0$ och $a-\frac{1}{2}>0$ , dvs $a>0$ och $a>\frac{1}{2}$ , dvs $a>\frac{1}{2}$

Sammantaget ger det oss att ekvationen har två reella lösningar då antingen $a<0$ eller $a>\frac{1}{2}$

-------------------------------------------

Vi undersöker sedan fallet en reell lösning (dubbelrot), dvs $D=0$

Då gäller att $a(a-\frac{1}{2})=0$

Enligt nollproduktmetoden så ger det oss de två möjligheterna $a=0$ och $a-\frac{1}{2}=0$ , dvs $a=0$ och $a=\frac{1}{2}$ .

Sammantaget ger det oss att ekvationen har en reell lösning (dubbelrot) då antingen $a=0$ eller $a=\frac{1}{2}$

--------------------------

Egentligen kan vi sluta här, för resten av fallen, dvs $0<a<\frac{1}{2}$ måste ge oss det tredje alternativet, att ekvationen saknar reella lösningar.

Men för att visa hur den beräkningen går till så tar jag med den ändå.

Vi undersöker fallet ingen reell lösning, dvs $D<0$

Då gäller att $a(a-\frac{1}{2})<0$

För att en produkt av två faktorer ska vara mindre än 0 måste det gälla att de båda faktorerna har olika tecken, dvs antingen är den ena faktorn mindre än 0 och den andra faktorn större än 0 eller så är det tvärtom.

Det ger oss följande två möjligheter:

$a<0$ och $a-\frac{1}{2}>0$ , dvs $a<0$ och $a>\frac{1}{2}$ . Dessa två villkor motsäger varandra så det fallet kan inte inträffa.

eller

$a>0$ och $a-\frac{1}{2}<0$ , dvs $a>0$ och $a<\frac{1}{2}$ , dvs $0<a<\frac{1}{2}$ . Det är en möjlighet.

Sammantaget ger det oss att ekvationen saknar reella lösningar då $0<a<\frac{1}{2}$

-------------------------

Om vi lägger ihop allting så får vi nu följande:

$a<0$ : Två reella lösningar

$a=0$ : En reell lösning (dubbelrot)

$0<a<\frac{1}{2}$ : Inga reella lösningar

$a=\frac{1}{2}$ : En reell lösning (dubbelrot)

$a>\frac{1}{2}$ : Två reella lösningar

Yngve skrev:
Nej det är inte rätt.
Lösningsförslag. Läs, förstå och försök att göra på liknande sätt i dina egna lösningar framöver, dvs skriv förklarande text och skriv lösningen steg för steg.
Ekvationen är $2x^2+4ax+a=0$
Dividera båda sidor med 2:
$x^2+2ax+\frac{a}{2}=0$
Pq-formeln ger oss lösningarna
$x=-a\pm\sqrt{D}$ , där diskriminanten $D=a^2-\frac{a}{2}=a(a-\frac{1}{2})$
Vi vet att vi har
två reella lösningar då $D>0$
en reell lösning (dubbelrot) då $D=0$
inga reella lösningar då $D<0$
Frågan gäller hur värdet på $a$ påverkar antalet reella lösningar.
-------------------------------------------
Vi undersöker först fallet två reella lösningar, dvs $D>0$
Då gäller att $a(a-\frac{1}{2})>0$
För att en produkt av två faktorer ska vara större än 0 måste det gälla att båda faktorerna har samma tecken, dvs antingen är båda faktorerna mindre än 0 eller så är båda faktorerna större än 0.
Att båda faktorerna är mindre än 0 ger villkoren $a<0$ och $a-\frac{1}{2}<0$ , dvs $a<0$ och $a<\frac{1}{2}$ , dvs $a<0$
Att båda faktorerna är större än 0 ger villkoren $a>0$ och $a-\frac{1}{2}>0$ , dvs $a>0$ och $a>\frac{1}{2}$ , dvs $a>\frac{1}{2}$
Sammantaget ger det oss att ekvationen har två reella lösningar då antingen $a<0$ eller $a>\frac{1}{2}$
-------------------------------------------
Vi undersöker sedan fallet en reell lösning (dubbelrot), dvs $D=0$
Då gäller att $a(a-\frac{1}{2})=0$
Enligt nollproduktmetoden så ger det oss de två möjligheterna $a=0$ och $a-\frac{1}{2}=0$ , dvs $a=0$ och $a=\frac{1}{2}$ .
Sammantaget ger det oss att ekvationen har en reell lösning (dubbelrot) då antingen $a=0$ eller $a=\frac{1}{2}$
--------------------------
Egentligen kan vi sluta här, för resten av fallen, dvs $0<a<\frac{1}{2}$ måste ge oss det tredje alternativet, att ekvationen saknar reella lösningar.
Men för att visa hur den beräkningen går till så tar jag med den ändå.
Vi undersöker fallet ingen reell lösning, dvs $D<0$
Då gäller att $a(a-\frac{1}{2})<0$
För att en produkt av två faktorer ska vara mindre än 0 måste det gälla att de båda faktorerna har olika tecken, dvs antingen är den ena faktorn mindre än 0 och den andra faktorn större än 0 eller så är det tvärtom.
Det ger oss följande två möjligheter:
$a<0$ och $a-\frac{1}{2}>0$ , dvs $a<0$ och $a>\frac{1}{2}$ . Dessa två villkor motsäger varandra så det fallet kan inte inträffa.
eller
$a>0$ och $a-\frac{1}{2}<0$ , dvs $a>0$ och $a<\frac{1}{2}$ , dvs $0<a<\frac{1}{2}$ . Det är en möjlighet.
Sammantaget ger det oss att ekvationen saknar reella lösningar då $0<a<\frac{1}{2}$
-------------------------
Om vi lägger ihop allting så får vi nu följande:
$a<0$ : Två reella lösningar
$a=0$ : En reell lösning (dubbelrot)
$0<a<\frac{1}{2}$ : Inga reella lösningar
$a=\frac{1}{2}$ : En reell lösning (dubbelrot)
$a>\frac{1}{2}$ : Två reella lösningar

När du undersöker antalet oreella lösningar skriver du att svaret är att. 1/2 > a> 0 . Hur kan det stämma? Om a är större än en halv då kommer summan av talen inuti parentesen att alltid vara + dvs det finns 2 lösningar. Om jag tex skriver 0,8-0,5=0,3. Jag får en positiv lösning. Det blir inget negativt svar.? Jag förstår inte hur du kom framtill till att >1/2 >a>0varför just större än 0?

Jag tror att du bara har missförstått skrivsättet 0 < a < 1/2.

Det är bara ett kortare sätt att skriva "a > 0 och a < 1/2", dvs "a ligger mellan 0 och 1/2".

Exempel:

Talet a = 0,8 ligger alltså inte i det intervallet eftersom det inte uppfyller villkoret a < 1/2.
Talet a = -23 ligger inte heller i intervallet eftersom det inte uppfyller villkoret a > 0.
Däremot ligger talet a = 0,1 i intervallet eftersom det uppfyller båda villkoren, dvs 0 < 0,1 < 1/2.

jag har fortfarande svårt att se hur du kom fram till att 0 <a< 1/2 . Allt annat förstår jag

OK.

Vid vilket av följande steg i resonemanget tappar jag bort dig?

Vi undersöker fallet ingen reell lösning, dvs $D<0$ . Då gäller att $a(a-1/2)<0$ . Detta är en produkt av de två faktorerna $a$ och $a-1/2$ .
För att en produkt av två faktorer ska vara mindre än 0 måste det gälla att de båda faktorerna har olika tecken, dvs antingen är den ena faktorn mindre än 0 och den andra faktorn större än 0 eller så är det tvärtom.
Det ger oss följande två möjligheter: Antingen är $a<0$ och $a-1/2>0$ dvs $a<0$ och $a>1/2$ eller så är $a>0$ och $a-1/2<0$ , dvs $a>0$ och $a<1/2$ .
Den första möjligheten kan inte inträffa, eftersom $a$ inte kan vara både mindre än 0 och större än 1/2.
Den andra möjligheten kan dock inträffa, dvs att a är större än 0 och mindre än 1/2.
Sammantaget ger det oss att ekvationen saknar reella lösningar då $0<a<1/2$ .

Nu fattar jag! Tack :)