Undersökning av serie

Hej! Uppgiften lyder:

Undersök om följande serie är konvergent eller divergent:

$\sum_{k = 2}^{\infty} \frac{1}{(\ln k)^{100}}$ . Bokens lösningsförslag är som följer:

$\frac{1}{(\ln k)^{100}} \to 0 d å k \to \infty$ men mycket långsamt, t.ex. $\frac{1}{(\ln k)^{100}} > \frac{1}{k} \Leftrightarrow (\ln k)^{100} < k \Leftrightarrow \ln k < k^{1 / 100} \Leftrightarrow \frac{\ln k}{k^{1 / 100}} < 1$ som gäller för stora k ty $\frac{\ln k}{k^{1 / 100}} \to 0 d å k \to \infty$ .

$\sum_{k = 1}^{\infty} \frac{1}{k}$ divergent $\Rightarrow$ den givna serien är divergent.

Jag förstår inte deras resonemang. På vilket sätt går $\frac{1}{(\ln k)^{100}}$ mot 0 väldigt långsamt? Det är väl ändå tvärtom? När k > 2 så växer den ju löjligt fort. Olikheten $\frac{1}{(\ln k)^{100}} > \frac{1}{k}$ tycker jag också ser helt tokig ut. Det gäller ju endast för k = 2?

Någon som tycker sig kunna bringa klarhet till lösningsförslaget? Är det bara jag som helt missuppfattar resonemanget, eller vad är det frågan om?

Du har att

ln(x)/x^a

går mot 0 då x går mot oändligheten för alla a > 0.

Dr. G skrev:
Du har att
ln(x)/x^a
går mot 0 då x går mot oändligheten för alla a > 0.

Jo, det är jag med på. Men sättet de tar sig dit på tycker jag är underligt. I mitt huvud stämmer inte olikheterna som de använder för att skriva om uttrycket...

Vad är det som växer löjligt fort om k > 2? Funktionen $f(k)=\frac{1}{(\ln k)^{100}}$ blir ju bara mindre och mindre ju större k blir, så det kan inte vara den funktionen du menar.

Smaragdalena skrev:
Vad är det som växer löjligt fort om k > 2? Funktionen $f(k)=\frac{1}{(\ln k)^{100}}$ blir ju bara mindre och mindre ju större k blir, så det kan inte vara den funktionen du menar.

Slarvigt uttryckt från min sida. Menar att uttrycket i nämnaren växer fort, och att kvoten därför går mot 0 fort, snarare än "mycket långsamt" som det står i lösningsförslaget.

Det är inte möjligen så att det står $\ln k^{100}$ i stället i nämnaren?

Smaragdalena skrev:
Det är inte möjligen så att det står $\ln k^{100}$ i stället i nämnaren?

Det skulle kunna vara ett feltryck i boken och att det är som du säger. Då går ju uttrycket mot 0 betydligt långsammare, men olikheten de använder stämmer fortfarande inte...

Kan du lägga in en bild från boken?

För stora k blir tillslut

ln(k)^100 < k

så alltså

1/ln(k)^100 > 1/k

Serien med 1/k är divergent, så då blir även den här serien divergent.

Smaragdalena skrev:
Kan du lägga in en bild från boken?

Bifogar uppgift och ledning.

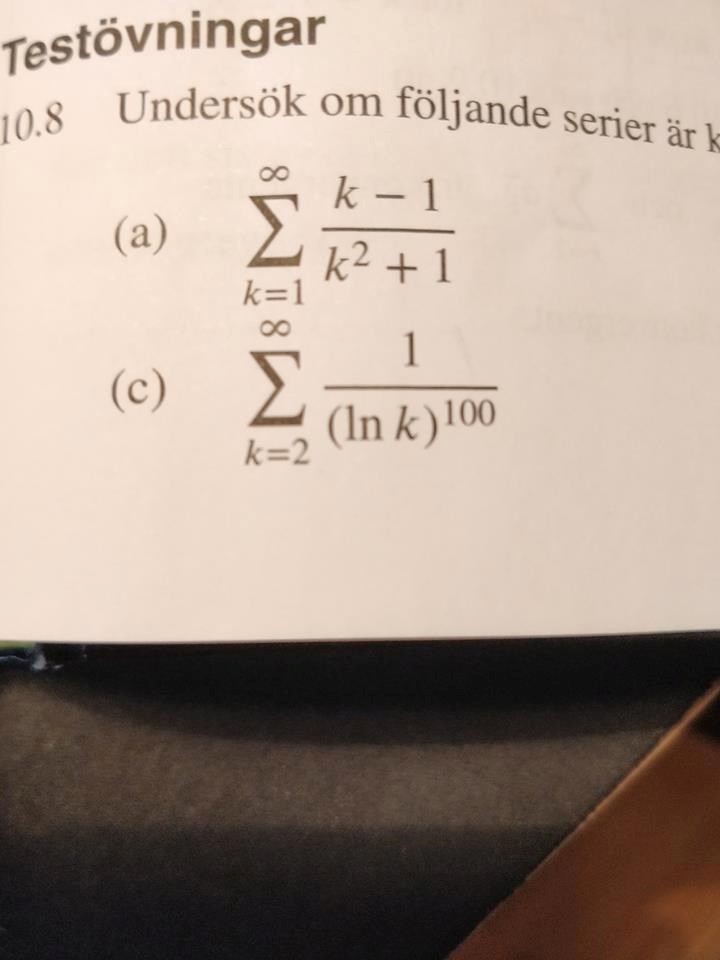
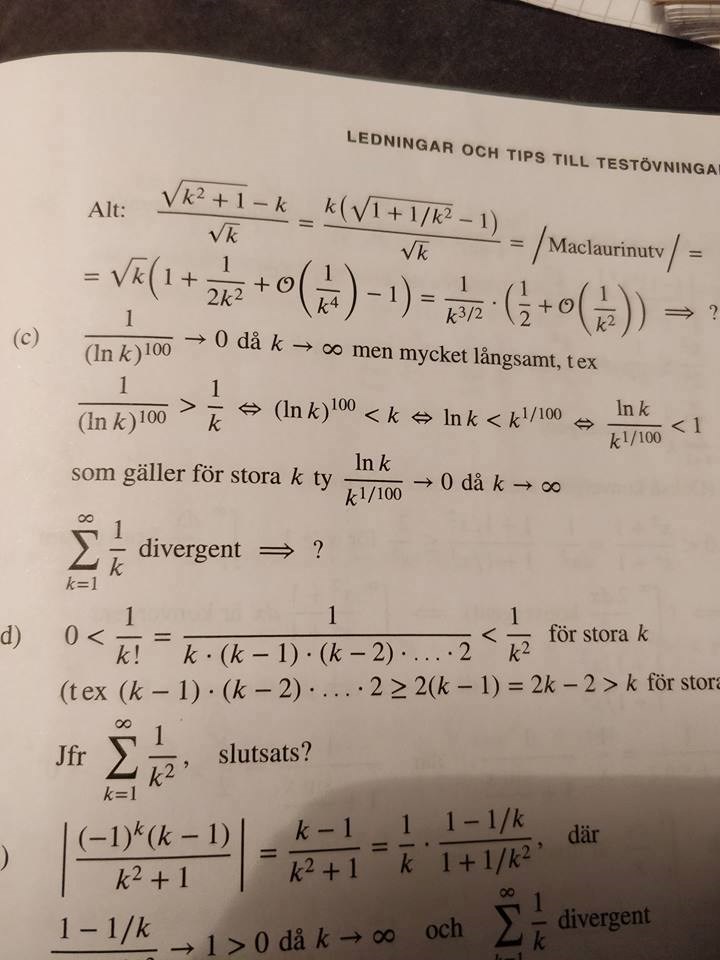
Dr. G skrev:
För stora k blir tillslut
ln(k)^100 < k
så alltså
1/ln(k)^100 > 1/k
Serien med 1/k är divergent, så då blir även den här serien divergent.

Tack, det är nog jag som har tänkt lite för ytligt och jämfört olikheten lite snabbt för olika k. Det står ju i lösningsförslaget att det gäller "för stora k". Jag tänkte inte riktigt på att olikheten bara gäller för tillräckligt stora k.

Svara

Visa senaste svar