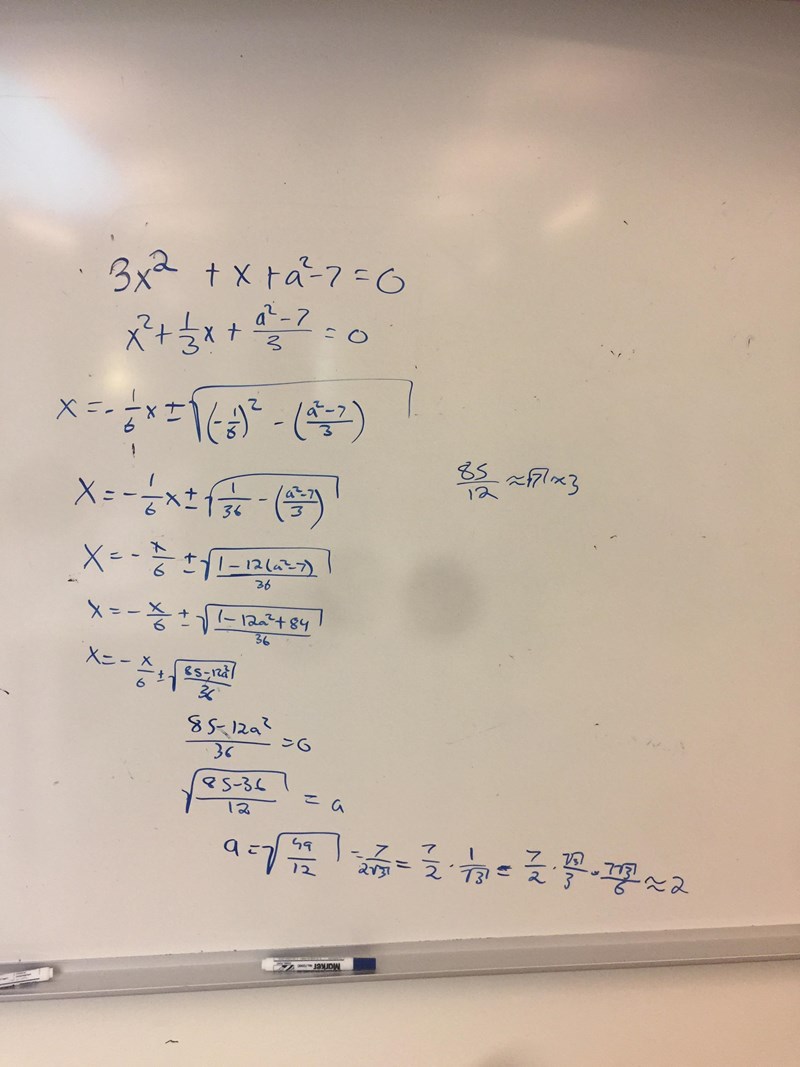Uppgift 22 på KTH/Chalmers matematik och fysikprov 2015, mattedel

Välkommen till Pluggakuten!

Flyttade tråden från Kluringar till Ma4, som är den matematik-nivå man beräknas behärska om man söker till teknisk högskola. I själva verket räcker det gott med Ma2 för den här uppgiften.

Hur har du tänkt själv? Det står i Pluggakutens regler att du skall visa hur du har försökt och hur långt du har kommit.  /moderator

Euleroid skrev:

Ange det största heltal a sådant att ekvationen 3x^2 + x + a^2 − 7 = 0 har minst en reell lösning.

Skulle någon kunna visa mig hela uträckningen på denna ekvation?

Kommer inte längre än detta i denna uträckning

2ax+7 står det inte i uttrycket som du hade i början.

Laguna skrev:

2ax+7 står det inte i uttrycket som du hade i början.

Oj hoppsan.

Euleroid skrev:

Euleroid skrev:

Ange det största heltal a sådant att ekvationen 3x^2 + x + a^2 − 7 = 0 har minst en reell lösning.

Skulle någon kunna visa mig hela uträckningen på denna ekvation?

Kommer inte längre än detta i denna uträckning

Du ska inte ha med x under rottecknet.

Laguna skrev:

Du ska inte ha med x under rottecknet.

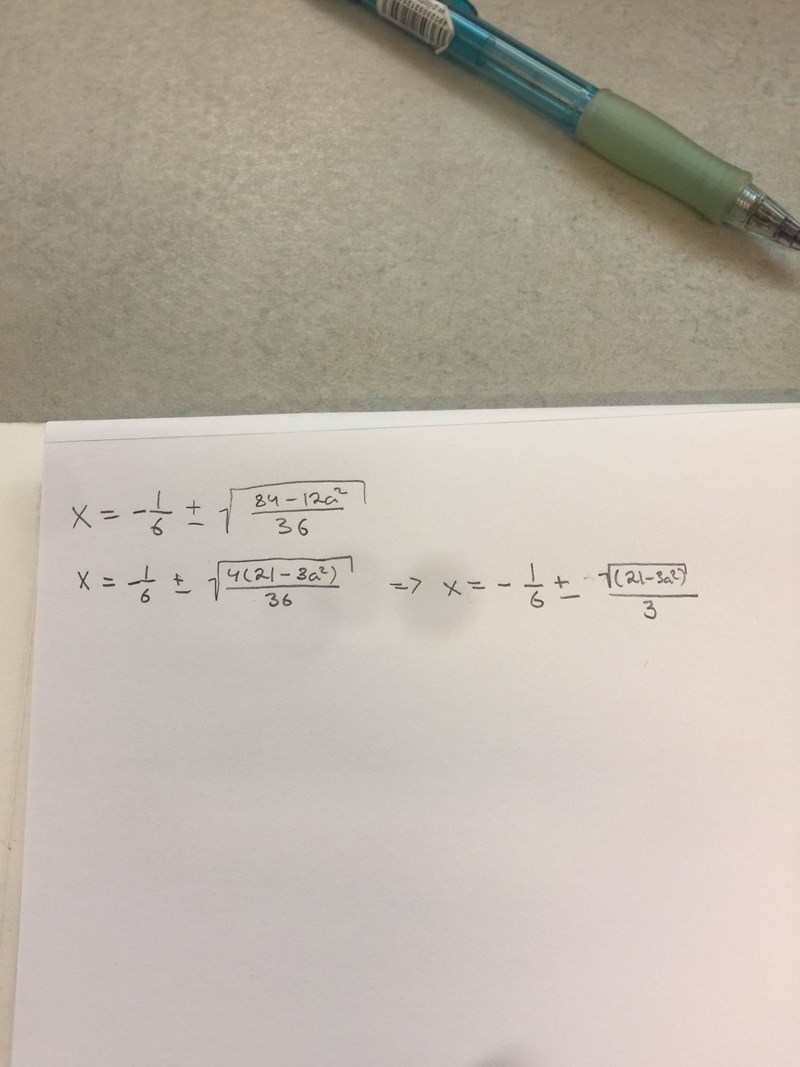
För vilka värden på a är uttrycket under rottecknet icke-negativt? D v s för vilka värden på a finns det reella rötter?

Smaragdalena skrev:

För vilka värden på a är uttrycket under rottecknet icke-negativt? D v s för vilka värden på a finns det reella rötter?

Är det då a = sqrt(7)

Det finns många olika värden på a som ger reella rötter, inte bara ett värde.

Smaragdalena skrev:

Det finns många olika värden på a som ger reella rötter, inte bara ett värde.

Hur kan man begränsa det till att specifikt söka det största a-värdet?

Förlåt, jag mindes frågan fel. De frågade bara efter ett största heltal a, inte alla värden på a som min minnesbild var.

Smaragdalena skrev:

Förlåt, jag mindes frågan fel. De frågade bara efter ett största heltal a, inte alla värden på a som min minnesbild var.

Det stämmer

Kommer inget vidare med denna uppgift, skulle någon kunna ge mig fler tips.

Svaret ska bli två. Eftersom man söker efter ett heltalsvärde, tänker jag rätt?

Det går väldigt fort där på slutet.

Hur kan du få

$\dfrac{85-12a^2}{36}=0$

till

$\sqrt{\dfrac{85-36}{12}}=a$

Det är tyvärr fel.

(Dock avrundas det riktiga $a$-värdet också nedåt till två, men det är en ren tillfällighet att du fått rätt svar)

85 - 12a²  = 36, 85 - 36 = 12a² => a = sqrt((85 - 36)/12))

Det stämmer inte.

Om du multiplicerar båda led med $36$ får du ju:

$\dfrac{85-12a^2}{36}\cdot36=0\cdot36$

$85-12a^2=0$

Du verkar ha räknat som om det stod $1$ istället för $0$ i högerled.

AlvinB skrev:

Det stämmer inte.

Om du multiplicerar båda led med $36$ får du ju:

$\dfrac{85-12a^2}{36}\cdot36=0\cdot36$

$85-12a^2=0$

Du verkar ha räknat som om det stod $1$ istället för $0$ i högerled.

Det stämmer

Vet du hur andragradare med positiv koefficient på x^2-termen ser ut på en plot? För då hade du sett att a dyker upp som en konstant, den flytta parabeln uppåt eller nedåt när du ändrar värden på a. 

Eftersom du vill ha minst en reell lösning så är detta när du stoppar in ett a-värde så att parabeln får en dubbelrot på x-axeln. D.v.s när du gör pq-formeln eller kvadrat kompliterar så ska roten ur uttrycket vara lika med noll. Sedan avrundar det talet neråt till närmsta heltal under.

Jag skulle börja med att rita upp kurvan 3x²+x-7=0, d v s att a = 0 och undersöka vilket y-värde jag har i minimipunkten (jag vet ju att det är en minimipunkte eftersom koefficienten för x²-termen är positiv).Man behöver inte ens lösa hela PQ-formeln för att få fram vilket som är x-värdet för minimipunkten. Sedan borde det gå snabbt att undersöka vilken kvadrat som är den största som inte gör att minimivärdet blir positivt.

När du använder pq-formeln är det det som står under rottecknet (det har något fint namn som undgår mig just nu) som bestämmer om du har två reella rötter, en reell (dubbel) rot eller komplexa rötter. Det vill säga om:$$\begin{gathered} (\frac{p}{2}{)}^2-q = 0 en dubbelrot \\ (\frac{p}{2}{)}^2-q > 0 två reella rötter \\ (\frac{p}{2}{)}^2-q < 0 två komplexa rötter \end{gathered}$$

Så du hamnar i att om $85-12a^2\ge 0$ har denna minst en reell lösning.

Hej!

Med kvadratkomplettering kan ekvationen skrivas

    $(6x+1)^2+12a^2-85=0.$

Kvadraten $(6x+1)^2$ är aldrig negativ så man ser direkt följande:

• Om $12a^2-85>0$ saknas reella lösningar.
• Om $12a^2-85=0$ har ekvationen en enda reell lösning $x=-1/6$.
• Om $12a^2-85<0$ har ekvationen två olika reella lösningar.

Själva uppgiften handlar nu om att finna det största heltal $a$ sådant att

    $12a^2-85\leq0$.

Notera att $85=12\cdot 7+1$ så olikheten kan skrivas $12(a^2-7)-1\leq0$. Finns det några heltal som uppfyller denna olikhet?

Får olikheten till att bli a = sqrt(85/12)

AndersW skrev:

När du använder pq-formeln är det det som står under rottecknet (det har något fint namn som undgår mig just nu) ...

Det heter diskriminant.

Euleroid skrev:

Får olikheten till att bli a = sqrt(85/12)

Nej, det är en lösning till likheten. Vilket är nu det största heltal som uppfyller olikheten?

Blir lösningen till olikheten a större eller lika med sqrt(85/12)? Om det är så borde detta innebära att det största heltal som uppfyller detta är 2.

Euleroid skrev:

Blir lösningen till olikheten a större eller lika med sqrt(85/12)? Om det är så borde detta innebära att det största heltal som uppfyller detta är 2.

Ja.

Jag skulle sökt minimum:

$b=\min_x (3x^2+x-7)$

Sedan söks $a$ sådant att:

$a^2=-b$

och avrundning sker nedåt av lösningen till närmsta heltal ($a>0$).

Tack för hjälpen laguna :). Bra idé tomast80.

Olikheten $12(a^2-7)\leq 1$ är samma sak som olikheten $a^2\leq 7+1/12.$  Det finns fem heltal som uppfyller denna olikhet: $a\in\{-2, -1, 0, 1, 2\}.$  Det största av dessa är uppenbarligen $2$ som därför är svaret på den ställda frågan.