Uppgift 2360 medeltemperatur (Matematik/Matte 4)

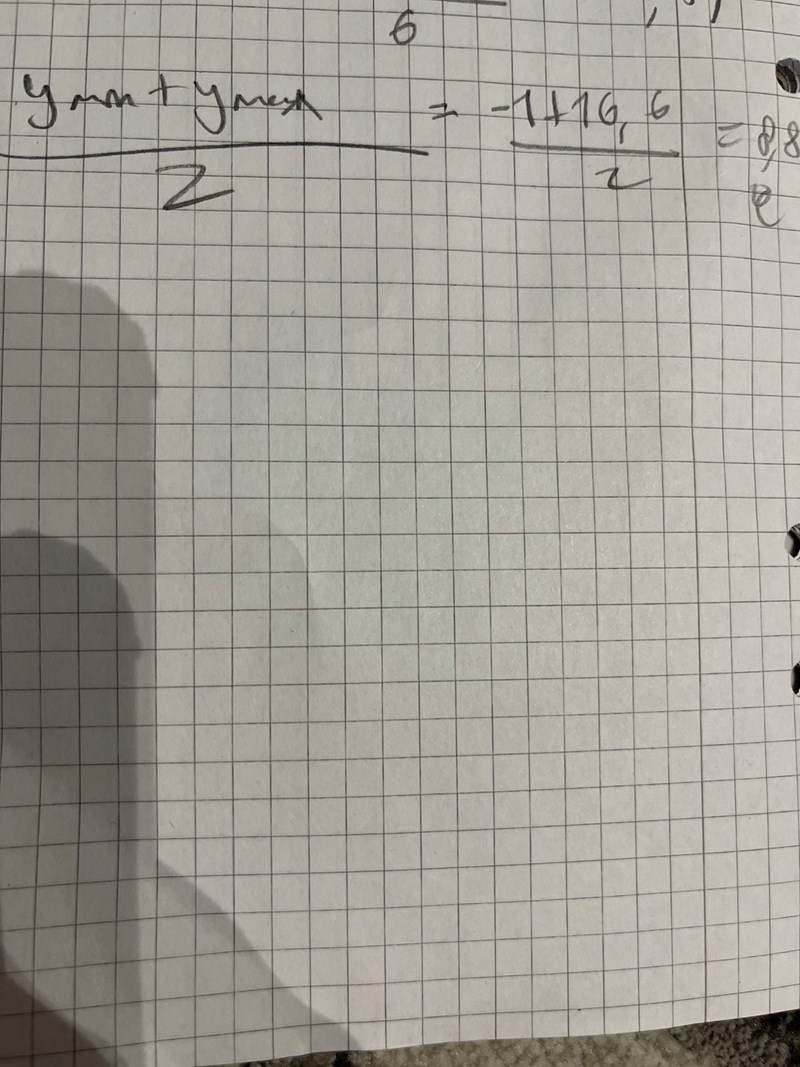
Det är rätt att tänka (T_max+T_min)/2.

Men du behöver inte beräkna vare sig T_max eller T_min utan du kan direkt se vad dessa värden är bara genom att titta på uttrycket för T.

Om du skissar grafen till T så ser du varför din första ansats inte var rätt.

Jag har försökt skissa grafen på min grafräknare men inget kommer fram

Du kan inte få samma värde oavsett x. Kan du haft räknaren på grader istf radianer? Men du behöver inte räkna ut något!

När du ser en funktion på formen
Asin(Bx+C)+D
(eller cos, spelar ingen roll)
ska du tänka vad de olika talen står för:
A är amplituden. Eftersom sin() svänger mellan -1 och 1 så kommer funktionen Asin() att svänga mellan -A till A.
B är perioden. Om B=1 är perioden 2pi, är B=2 är perioden pi osv
C är en förskjutning i x-led (kurvans förskjutning beror också på B men det behöver vi inte ta just nu)
D är förskjutningen i y-led. Är D=0 så svänger kurvan runt 0, som en vanlig sin(). Om D=13 svänger kurvan runt 13, den har lika många värden över 13 som värden under 13.

Om ovanstående är glasklart kan vi titta på funktionen (om det inte är glasklart, läs igen, rita med geogebra, blir tydligare än på grafräknaren):
T(x)=8+8,6cos(pi*(x-7)/6)
D=8 --> kurvan svänger runt 8. 8 är medelvärdet. 8 är medeltemperaturen.
A=8,6 --> amplituden är 8,6. Det högsta värdet cos() kan anta är 1. Då är det högsta värdet som 8,6*cos() kan anta 8,6. Eftersom kurvan är förskjuten i y-led av D med 8 är det det högsta värdet för hela funktionen 8+8,6=16,6
På samma sätt är det minsta värdet 8-8,6=-0,6

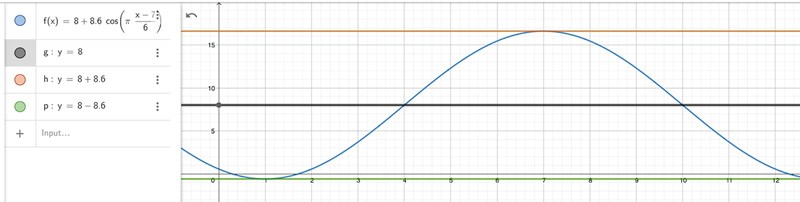
Hur kan du i grafen se att kurvan svänger runt 8.8? Jag ser att grafen fortsätter gå upp / stiga men inte att den svänger..? Grafen svänger ju vid maxpunkt då y=16.6

Läs igenom noga vad jag skrev. Titta inte på grafen, den är där som komplement. Titta på funktionen. Var finns talet 8 i funktionen?

I den här meningen ”Om D=13 svänger kurvan runt 13, den har lika många värden över 13 som värden under 13.” menar du att D ger oss ett jämviktsläge? Dvs att medeltemperaturen ges av D? Varför är det så

Katarina149 skrev:
I den här meningen ”Om D=13 svänger kurvan runt 13, den har lika många värden över 13 som värden under 13.” menar du att D ger oss ett jämviktsläge? Dvs att medeltemperaturen ges av D? Varför är det så

Ja. Det är så funktionen är definierad. I ditt fall är temperaturen "medeltemperaturen plusminus nånting som avviker högst 8,6 grader från medeltemperaturen".

Jag har löst b. Men jag hade bara fastnat på a.
Men hur kommer det sig att D ger oss medeltemperaturen?

Om du vill beräkna medeltemperaturen algebraiskt så kan du integrera fram den. Integrera då T(x) från x = 0 till x = 12 och dela resultatet med 12.

Annars kan du inse att temperaturgrafen spenderar lika mycket tid ovanför som under jämviktsnivån 8° C och att dessa temperatursvängningar därför tar ut varandra.

Programmeraren skrev:
Du kan inte få samma värde oavsett x. Kan du haft räknaren på grader istf radianer? Men du behöver inte räkna ut något!

När du ser en funktion på formen
Asin(Bx+C)+D
(eller cos, spelar ingen roll)
ska du tänka vad de olika talen står för:
A är amplituden. Eftersom sin() svänger mellan -1 och 1 så kommer funktionen Asin() att svänga mellan -A till A.
B är perioden. Om B=1 är perioden 2pi, är B=2 är perioden pi osv
C är en förskjutning i x-led (kurvans förskjutning beror också på B men det behöver vi inte ta just nu)
D är förskjutningen i y-led. Är D=0 så svänger kurvan runt 0, som en vanlig sin(). Om D=13 svänger kurvan runt 13, den har lika många värden över 13 som värden under 13.

Om ovanstående är glasklart kan vi titta på funktionen (om det inte är glasklart, läs igen, rita med geogebra, blir tydligare än på grafräknaren):
T(x)=8+8,6cos(pi*(x-7)/6)
D=8 --> kurvan svänger runt 8. 8 är medelvärdet. 8 är medeltemperaturen.
A=8,6 --> amplituden är 8,6. Det högsta värdet cos() kan anta är 1. Då är det högsta värdet som 8,6*cos() kan anta 8,6. Eftersom kurvan är förskjuten i y-led av D med 8 är det det högsta värdet för hela funktionen 8+8,6=16,6
På samma sätt är det minsta värdet 8-8,6=-0,6

Hur ska jag kunna se att det är lika mycket mellan grafen där y=8 om jag inte har tillgång till geogebra. Exempelvis på ett prov där jag enbart får använda mig av min grafräknare. Den visar enbart det här

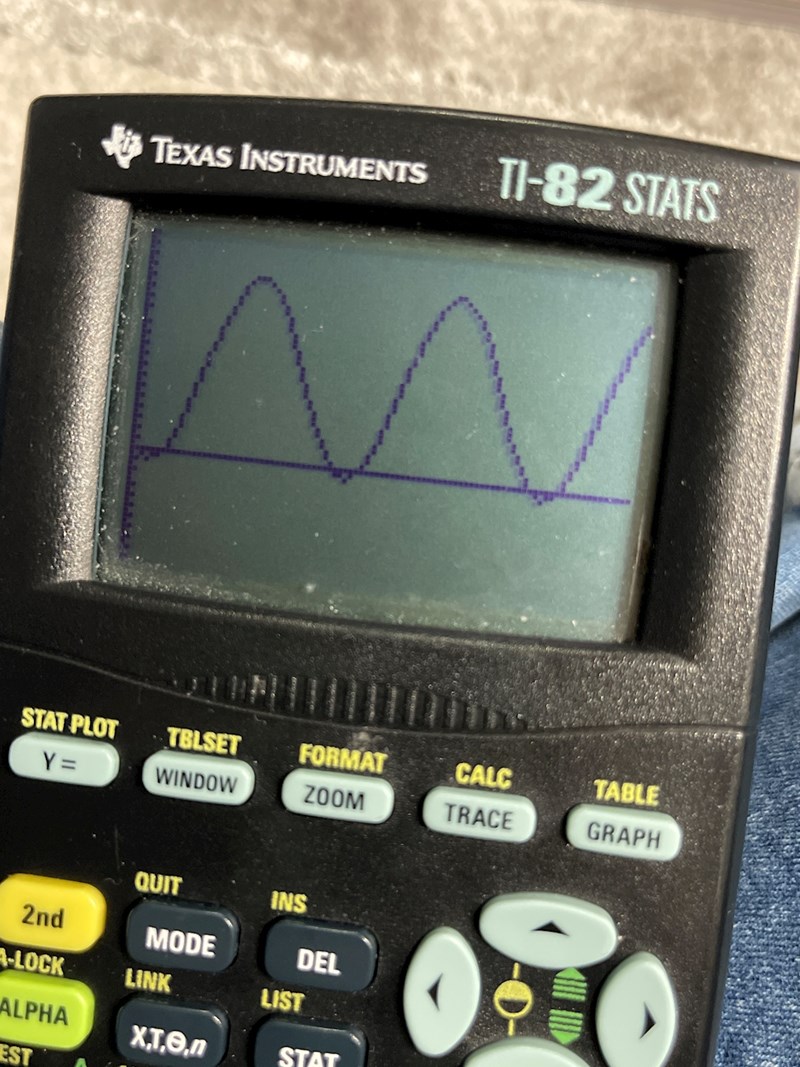Att integrera känner jag inte att jag Vill göra… Men hyrbilar jag avläsa svaret mha mitt diagram på bilden ovan

Hur ska jag kunna se att det är lika mycket mellan grafen där y=8 om jag inte har tillgång till geogebra. Exempelvis på ett prov där jag enbart får använda mig av min grafräknare. Den visar enbart det här

Lägg in linjen y = 8 också - eller lär dig att sinuskurvan har symmetri!

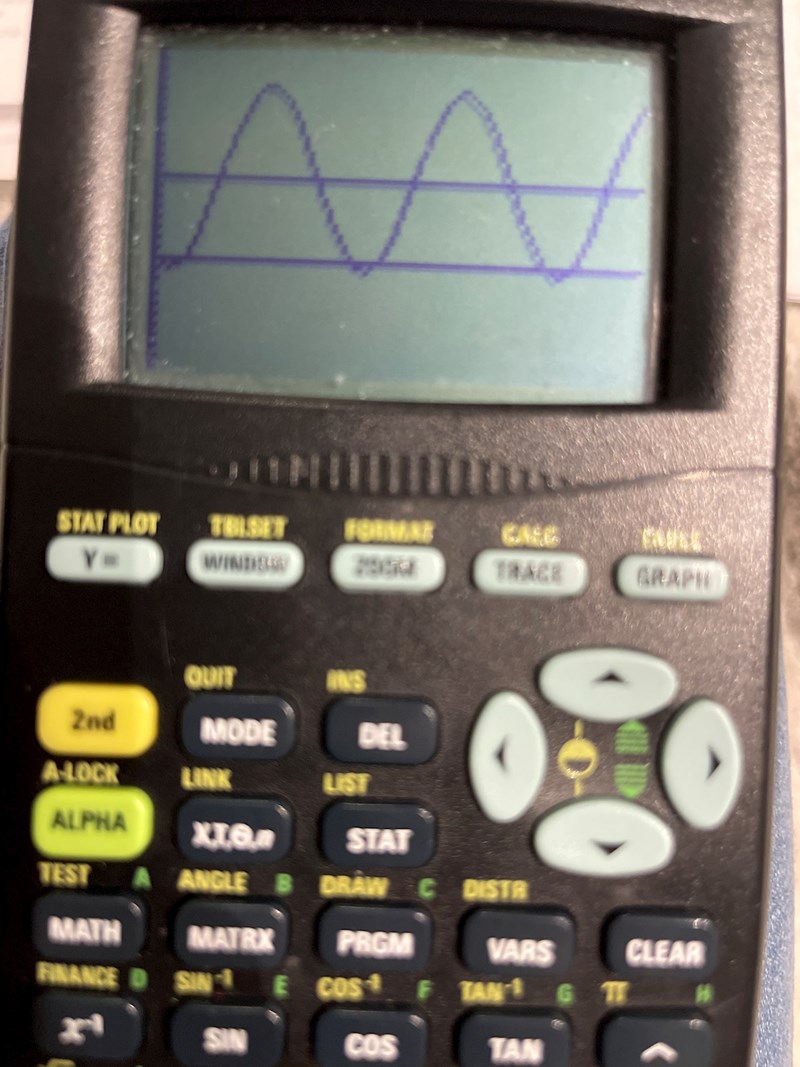Hur ska man veta att detta är ”mitten av grafen”?

När du skriver att sinuskurvan har symmetri. Hur menar du då?

Hur ska man veta att detta är ”mitten av grafen”?

Det ser du på att funktionen skrivs y = 8 + 8,6 cos(nånting)

När du skriver att sinuskurvan har symmetri. Hur menar du då?

Att den del av kurvan som är ovanför jämviktsläget är precis likadan som den delen som är under, bara förskjuten.

Vi prövar ett annat angreppssätt.

Är du med på att grafen till y = cos(x) tillbringar lika mycket tid ovanför som under x-axeln i ett intervall som motsvarar en hel period?
Är du med på att detta innebär att funktionens medelvärde i detta intervall är 0?

1. Ja jag är med på det

2. Nja , jag är osäker på vad du menar . Gärna om du förklarar med hjälp av en bild

Vi provar utan bild (dessa uppgifter är tänkta att lösas utan bild även om bilder förstås kan vara bra att förklara med ibland).

Du är med på att y=cos(x) tillbringar lika mycket tid ovanför som under x-axeln i ett intervall som motsvarar en hel period.
Om något är lika mycket på båda sidor 0 måste medelvärdet vara 0 eller hur?

Favorit i repris:
y(x)=Asin(Bx+C)+D (eller cos, spelar ingen roll)
A är amplituden. Eftersom sin() svänger mellan -1 och 1 så kommer funktionen Asin() att svänga mellan -A till A.
B är perioden. Om B=1 är perioden 2pi, är B=2 är perioden pi osv
C är en förskjutning i x-led (kurvans förskjutning beror också på B)
D är förskjutningen i y-led. Är D=0 så svänger kurvan runt 0, dvs dess medelvärde är 0. T ex sin(x) har D=0

Katarina149 skrev:
2. Nja , jag är osäker på vad du menar . Gärna om du förklarar med hjälp av en bild

Så här. Bilden visar grafen för cos(x) över en hel period (i det här fallet från pi/2 till 5pi/2).

Arean av område A är lika stor som arean av område B.

Det innebär att funktionens medelvärde i detta intervall är lika med 0.

Är du med på det?

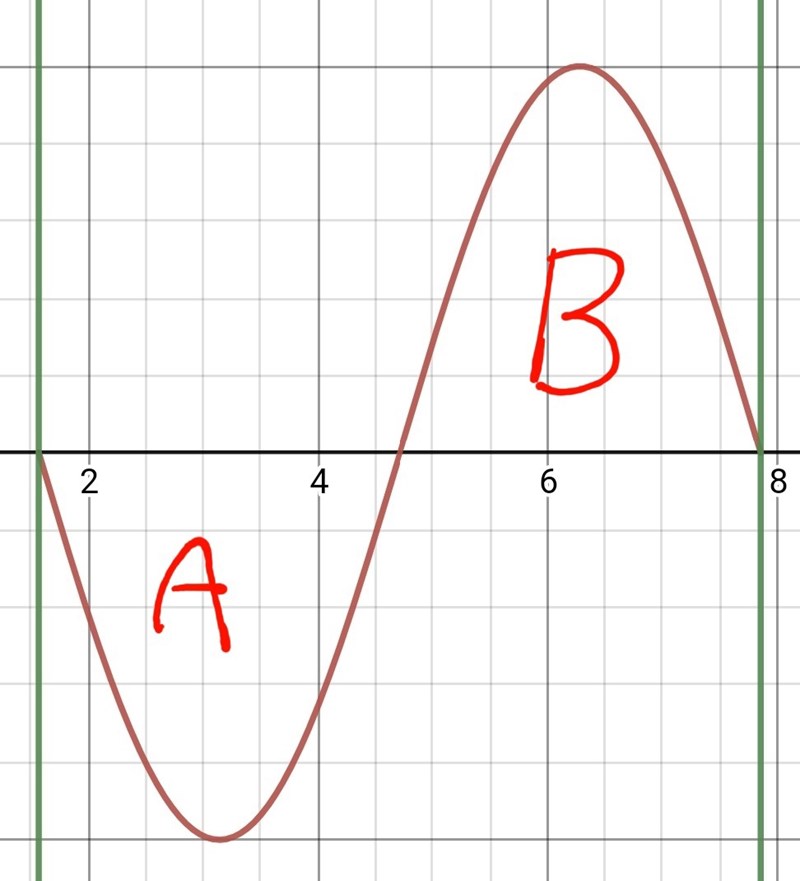
Ja, det är där grafen skärs i mitten där både A och B blir lika stor (får samma area)

Bra. Här har jag ritat samma funktion (dvs cos(x)) över ett annat helt intervall. Den här gången från -7pi/6 till 5pi/6.

Aran av område C är lika stor som summan av areorna av område A och B.

Det inmebär att funktionens medelvärde även i detta intervall är lika med 0.

Är du med på det?

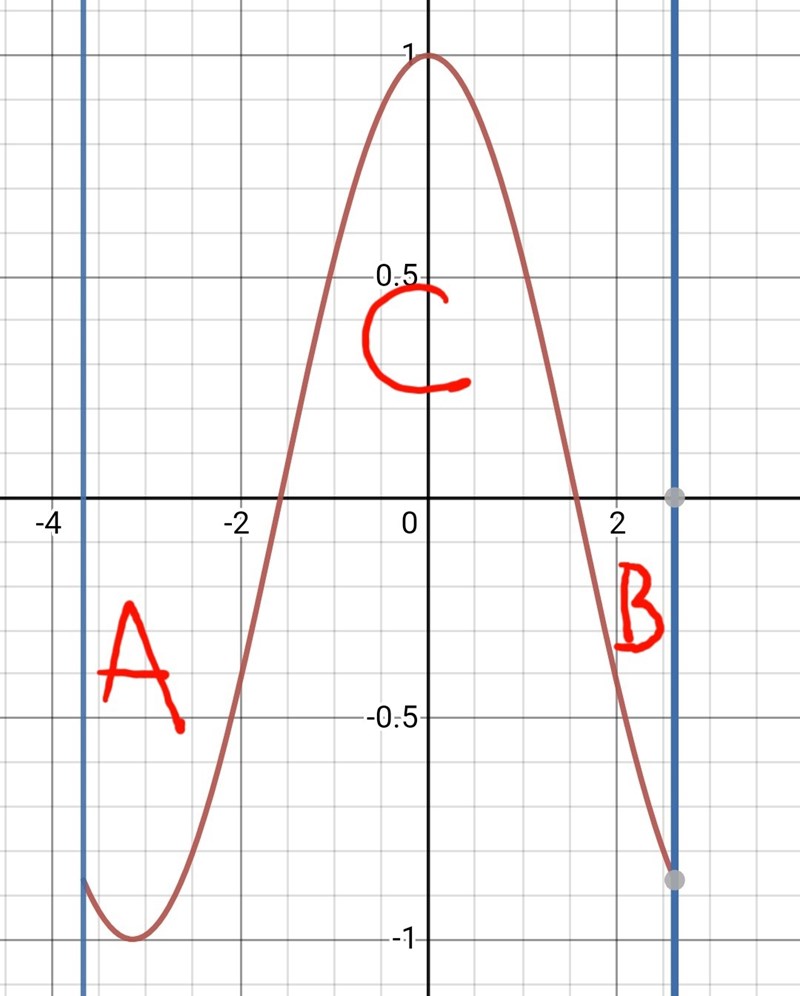
Hur kan du uppskatta att arean av A+B är lika stor som arean av C?

Inte uppskatta. Det går att se att de är det.

Så här:

Eftersom intervallet är en hel period så är funktionsvärdet vid den vänstra gränsen lika med funktionsvärdet vid den högra gränsen (sin(-7pi/6) = sin(5pi/6)).

Det betyder att om vi flyttar område B så att det ligger precis till vänster om område A så kommer grafen att se ut så här:

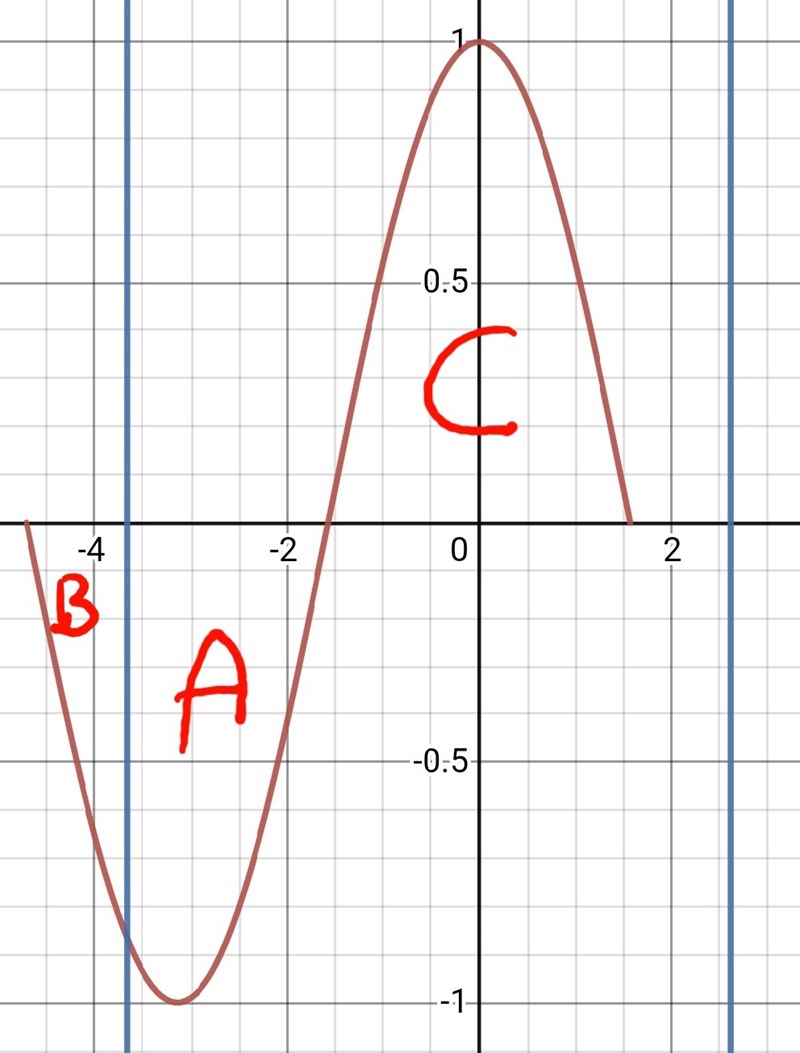
Situationen är då precis likadan som i det första exemplet - Hälften av perioden ligger grafen ovanför x-axeln och hälften av perioden ligger grafen under x-axeln.

Är du med på det?

jag hänger med på tankesättet. Men hur ska man veta när detta inte gäller. Dvs när det inte finns en ”jämviktsläge”?

Det gäller alltid om intervallet är ett helt antal perioder.

Hur menar du?

Om intervallet t.ex. är från 0 till p/2 så gäller det inte att arean ovanför x-axeln är lika stor som arean under x-axeln (för dåliggerju grafenaldrigens under x-axeln).

Men om intervallet är ett helt antal perioder, dvs från a till a+n•2pi så gäller det.

Förstår inte riktigt vad du menar

Att om man kapar av en bit (ej hel period) så kan medelvärdet ändras. I Yngves bild ovan, om det inte är en hel period kommer ju en del av någon a delareorna kapas bort. Ungefär som att medelvärdet av (-5,-3,0,3,5) är 0 men medelvärdet av (-5,-3,0,3) inte är noll

Men: hela resonemanget handlade om hur man ser att A*sin(Bx+C)+D har medelvärdet D. Det ser man eftersom
sin(x) har medelvärdet 0.
Amplituden A sträcker ut funktionen i y-led lika mycket åt båda hållen. dvs medelvärdet påverkas inte.
B och C är ovidkommande för medelvärdet eftersom de endast styr periodens längd och förskjutningen, både i x-led och inte i y-led.
Sammantaget har sin() medelvärdet 0, A*sin() medelvärdet 0, A*sin(Bx+C) medelvärdet 0 och då måste A*sin(Bx+C)+D ha medelvärdet D.
(Allt detta gäller när man har hela perioder och det har man nästan alltid (man har oftast oändligt många perioder)).

I 2360 är alltså medeltemperaturen 8 grader.

(1 <= x <= 12 ger att vinkeln antar värdena från -pi till pi-pi/6, dvs alla 12 steg jämt fördelade under 1 period. Detta behöver extremt sällan kontrolleras, sin/cos-funktioner används inte om det inte gäller).

Katarina149 skrev:
Förstår inte riktigt vad du menar

Rita grafen av en cosinusfunktion som sträcker sig över flera perioder, t ex.från 0 till 8pi.

Titta nu på olika intervall av grafen.

Om intervallet du tittar på inte är ett helt antal perioder (t ex. om du tar från 0 till pi/2 eller från pi/3 till 5pi/6) så kommer grafen inte tillbringa lika stor del av tiden ovanför som under x-axeln.

Om intervallet du tittar på är ett helt antal perioder (t ex. om du tar från 0 till 2pi eller från pi/4 till 17pi/4) så kommer grafen att tillbringa lika stor del av tiden ovanför som under x-axeln.

Pröva dig fram med olika intervallängder och olika placering av dessa intervall.

Får du fram samma sak som jag beskrev?

Kan du förklara dina exempel med hjälp av en bild?

Nu förstår jag inte.

Menar du alltså att du inte kan rita en cosinusfunktion från 0 till 8pi?
Menar du att du inte kan se hur den ser ut i intervallet 0 till pi/2?
Menar du att du inte kan se hur den ser ut i intervallet pi/3 till 5pi/6?
Menar du att du inte kan se hur den ser ut i intervallet 0 till 2pi?
Menar du att du inte kan se hur den ser ut i intervallet pi/4 till 17pi/4?

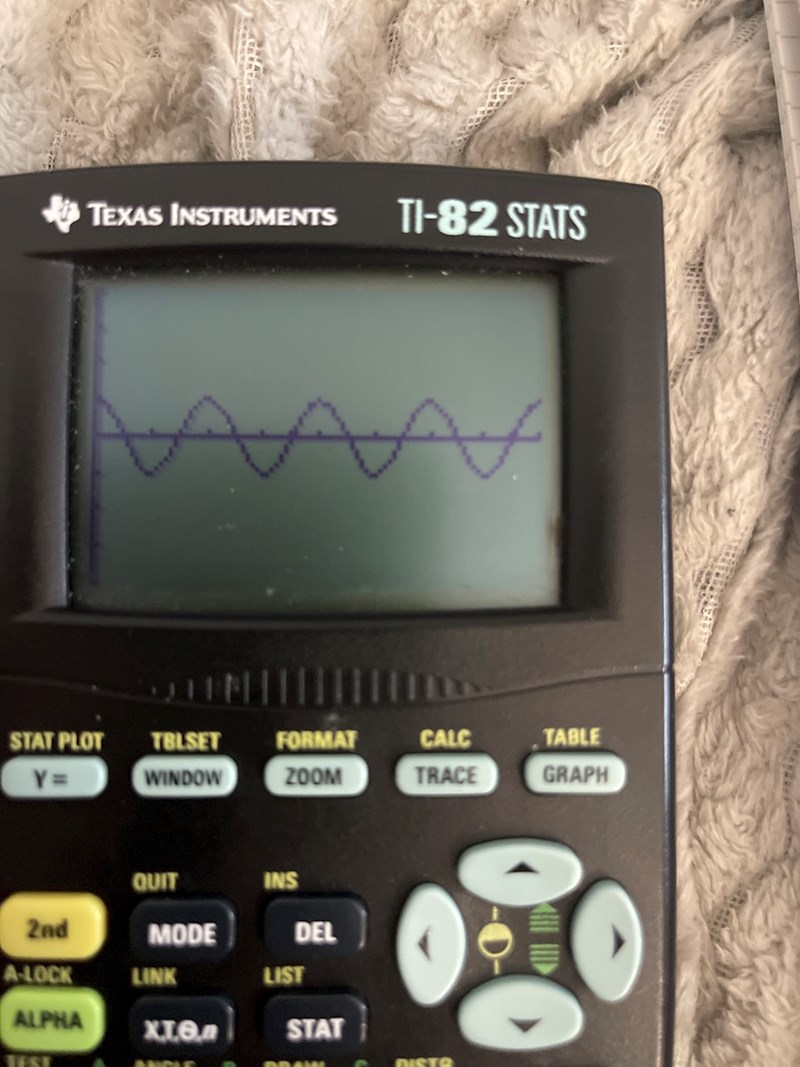Det här är grafen y•cos(x) mellan x intervallen 1140 och 0.
——

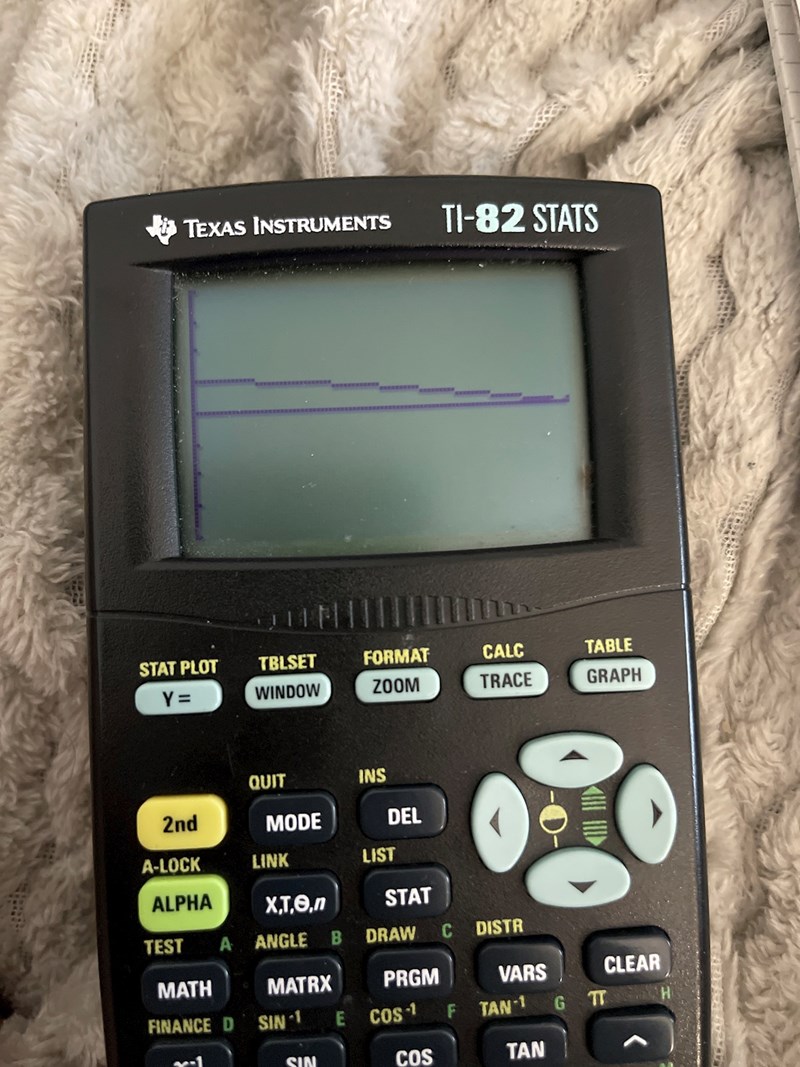Det här är grafen mellan x intervallet 0 till 90 grader

——————

Det här grafen mellan intervallet pi/3 och 5pi/6

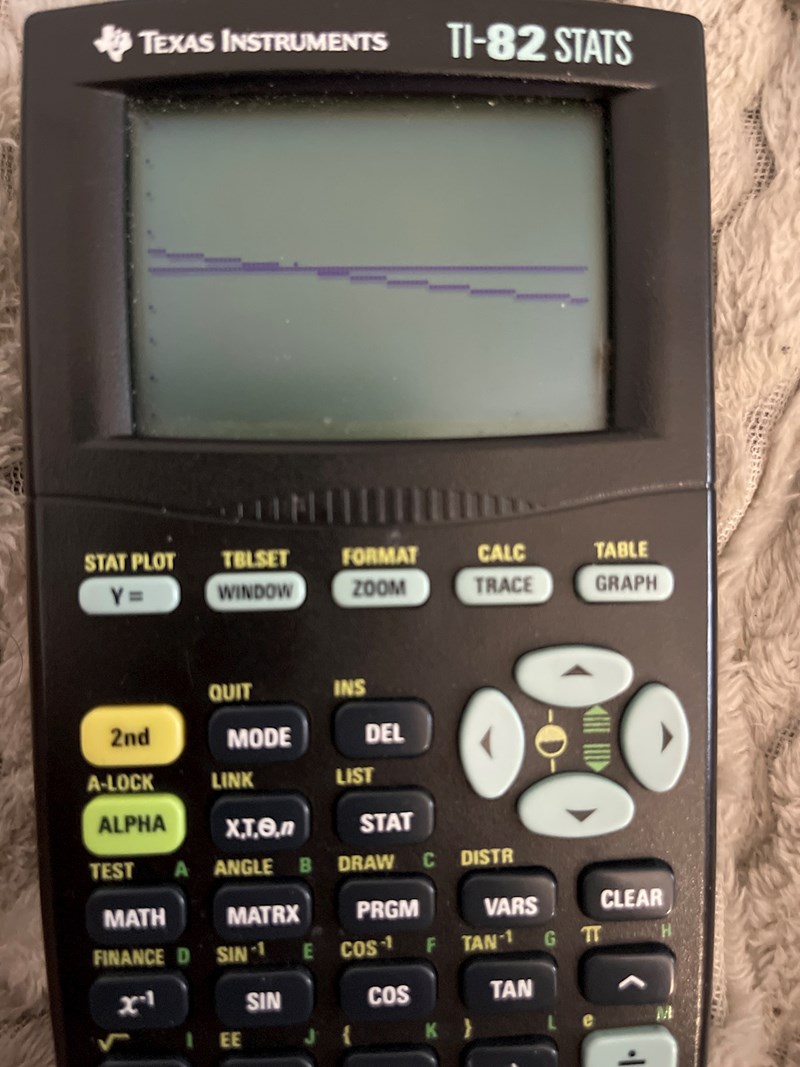Det jag kan konstatera är att i vissa grafer som exempelvis den som är precis ovan så befinner sig grafen i den första kvadranten inte lika mycket som i den fjärde kvadranten . I det här intervallet har grafen inte ”medelvärde”

Exakt så.

Slutsatsen är att en kurva som svänger lika mycket upp och ner under en period, t ex sin eller cos, kommer att ha medelvärdet 0 om man tittar på en hel period (eller flera hela perioder). Tittar man på en del av perioden kan medelvärdet vara "vad som helst".

Katarina149 skrev:
...

Det jag kan konstatera är att i vissa grafer som exempelvis den som är precis ovan så befinner sig grafen i den första kvadranten inte lika mycket som i den fjärde kvadranten . I det här intervallet har grafen inte ”medelvärde”

Ser du då vad jag menade med att medelvärdet är 0 om du tittar på ett intervall som utgörs av ett helt antal perioder, dvs ett intervall $[a,a+n\cdot2\pi]$ (där $a$ är ett godtyckligt tal)?

Och att medelvärdet inte är lika med 0 i alla andra fall?

Ja nu förstår jag!

Bra.

Betyder det att du även inser varför årsmedelvärdet av T(x) som är given i uppgiften är 8?

Man kan se att medelålders värdet är 8 om man ritar upp grafen på exempelvis en grafritare. Jag skulle enbart kunna veta att 8 är medelvärdet om jag hade till gång till en grafritare. Annars kan jag inte veta att just 8 är medelvärdet

OK då fortsätter vi att förklara så att du slipper använda grafräknare för att förstå att medelvärdet är 8.

Vi utgår från vår cosinusfunktion $f(v)=\cos(v)$ .

(Jag har bytt namn på vinkeln från x till v för att minska risken för förvirring i ett senare skede.)

Fråga 1: Visst var du med på att denna funktions medelvärde är 0 om intervallet är en hel period?

Nu ändrar vi amplituden från 1 till 8,6.

Dvs vi säger att $f(v)=8,6\cdot\cos(v)$

Fråga 2: Är du med på att även denna modifierade funktions medelvärde är 0 om intervallet är en hel period?

Fråga 1 : jag jag håller med .

Fråga 2 : varför är det så? Om 8.6 inte är ett heltal utan har decimaltal

Fråga 2: Detta eftersom funktionens graf fortfarande spenderar lika mycket tid ovanför som under v-axeln.

Det enda som skiljer cos(v) och 8,6*cos(v) är hur stora svängningarna är. Svängningarna har fortfarande samma periodicitet och de svänger fortfarande upp och ner kring v-axeln med lika stora utslag åt varje håll.

Illustration: cos(v) och 8,6*cos(v) i samma koordinatsystem.

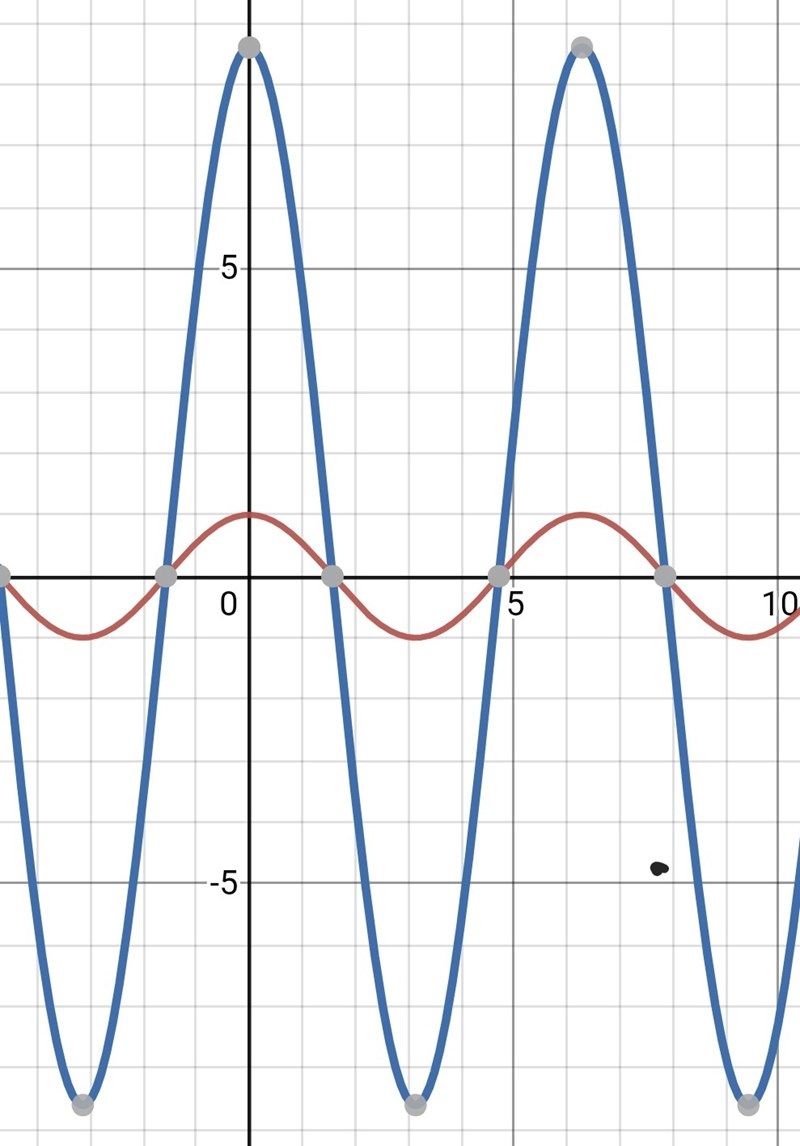
Hur ska man veta att funktionen 8.6cos(x) kommer att befinna sig lika mycket i första kvadranten som i fjärde? Är det för att funktionen cos(x) inte har någon förskjutning?

Vi pratar nu inte om kvadranter. Funktionen 8,6*cos(v) har ett (endimensionellt) värde som beror på vinkeln v. Detta värde ligger i intervallet [-8,6: 8,6]. Värdet ligger alltså ovanför eller under v-axeln, inte i någon kvadrant.

Vi kan göra en visualisering med hjälp av enhetscirkeln och kvadranter senare. Orsaken till att jag inte vill göra det nu är att vi då måste växla tankespår och jag är rädd att det kommer att förvirra mer än klargöra.

Jag fortsätter därför gärna med att visa det jag vill visa med hjälp av de grafer vi pratat om hittills.

Fråga 1: Ser du på graferna i mitt förra inlägg att cos(v) och 8,6*cos(v) endast skiljer sig åt avseende amplituden, dvs hur kraftiga svängningarna är?

Fråga 2: Ser du då att även grafen till 8,6*cos(v) spenderar lika mycket tid ovanför som under v-axeln (om intervallet är ett helt antal perioder)?

Yngve skrev:
Vi pratar nu inte om kvadranter. Funktionen 8,6*cos(v) har ett (endimensionellt) värde som beror på vinkeln v. Detta värde ligger i intervallet [-8,6: 8,6]. Värdet ligger alltså ovanför eller under v-axeln, inte i någon kvadrant.

Vi kan göra en visualisering med hjälp av enhetscirkeln och kvadranter senare. Orsaken till att jag inte vill göra det nu är att vi då måste växla tankespår och jag är rädd att det kommer att förvirra mer än klargöra.

Jag fortsätter därför gärna med att visa det jag vill visa med hjälp av de grafer vi pratat om hittills.

Fråga 1: Ser du på graferna i mitt förra inlägg att cos(v) och 8,6*cos(v) endast skiljer sig åt avseende amplituden, dvs hur kraftiga svängningarna är?

Fråga 2: Ser du då att även grafen till 8,6*cos(v) spenderar lika mycket tid ovanför som under v-axeln (om intervallet är ett helt antal perioder)?

Svar på fråga 1 : Ja det ser man

fråga 2 : Japp det ser man

OK bra.

Är du då även med på att medelvärdet av funktionen 8,6*cos(v) är lika med 0 om intervallet vi tittar på är en hel period?

Är osäker på om jag är med på tillfullo. Du kan testa med att ge test fråga så kan vi se om jag har förstått eller inte

Testfråga - Vilket område är störst: A eller B?

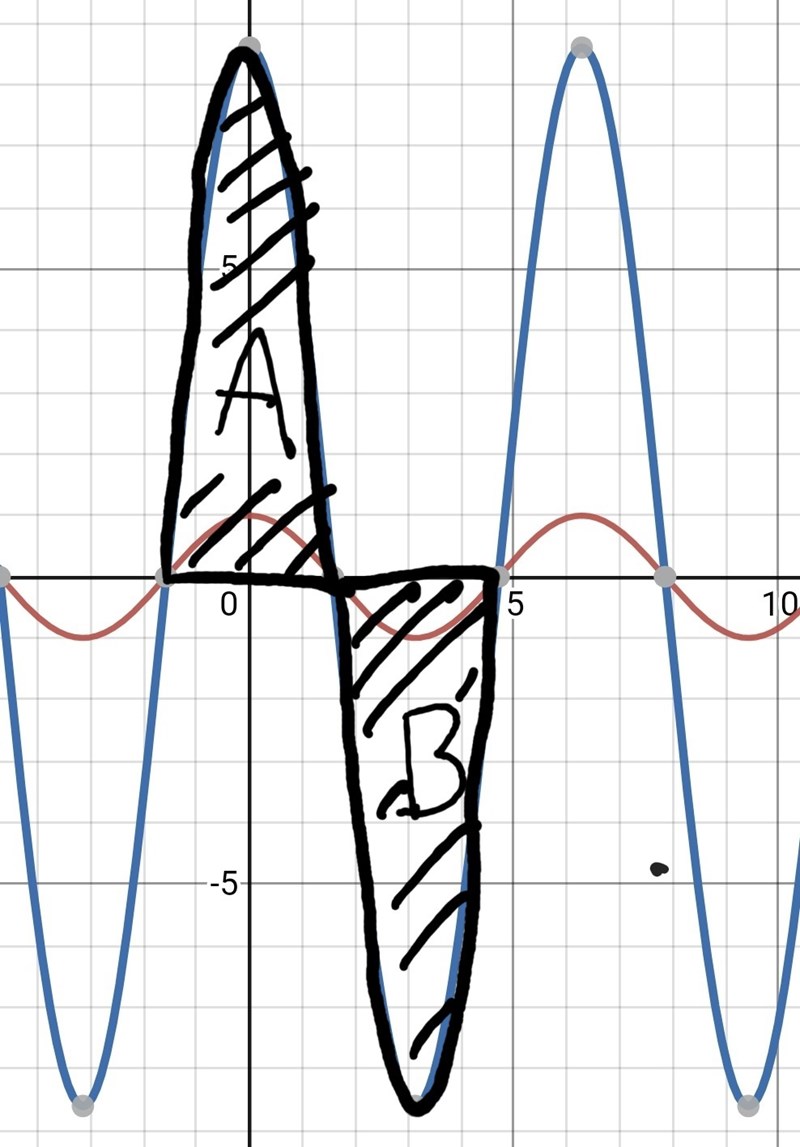
A och B är lika stora

Bra. Det betyder att funktionens medelvärde i det intervallet är lika med 0 eftersom grafen där tillbringar lika mycket tid ovanför som under linjen y = 0. Är du med på det?

Japp. Det är jag med på!

Bra. Då ändrar vi lite på funktionen igen. Vi lägger till ett konstant värde 8 så att funktionen nu blir 8+8,6*cos(v).

I bilden har jag ritat dess graf (i rött) i ett intervall som är en hel period.

Jag har även (i blått) ritat in linjen y = 8 som referens.

Koordinatsystemet är i svart.

Ser du att denna graf under en hel period spenderar lika mycket tid ovanför som under linjen y = 8?
Är du med på att detta innebär att funktionens medelvärde i det intervallet är lika med 8?

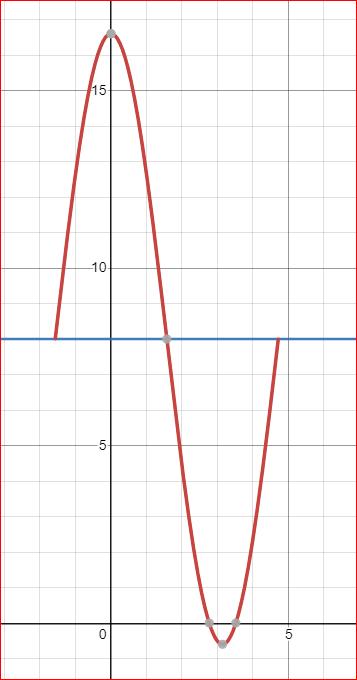
Jaha okej. Nu förstår jag. Alltså kan medelvärdet variera beroende på hur grafen ser ut. Är A•Sin(x+v)+D= y

Är D alltid lika med medelvärdet?

Bra.

Ja, om intervallet är ett helt antal perioder så är D alltid lika med medelvärdet (kallas även jämviktsläget).

Läs nu igenom alla svar i tråden igen och fråga om det är saker som du vill ha mer förklaring av.

Om du vill kan vi göra en illustration med hjälp av enhetscirkeln imorgon.

Hur menar du med ”helt antal perioder” menar du tex 2pi•n , 3pi•n , 4 pi•n…osv? Inte att det exempelvis ska vara 3.5pi•n , 1.2pi•n osv?

___
”Om du vill kan vi göra en illustration med hjälp av enhetscirkeln imorgon.”

Ja jättegärna .

Katarina149 skrev:
Hur menar du med ”helt antal perioder” menar du tex 2pi•n , 3pi•n , 4 pi•n…osv? Inte att det exempelvis ska vara 3.5pi•n , 1.2pi•n osv?

Nej, cos(v) har perioden 2pi, så 3pi•n är inte ett helt antal perioder.

Jag menar ett intervall vars längd är en multipel av 2pi, precis som jag skrev tidigare i det här svaret.

___
”Om du vill kan vi göra en illustration med hjälp av enhetscirkeln imorgon.”

Ja jättegärna .

== Steg 1: Funktionen cos(v) och en enhetscirkel ==

Vi ritar ett koordinatsystem där vi kallar den horisontella axeln för x och den vertikala axeln för y.

En radie i enhetscirkeln pekar ut en punkt på cirkeln som har koordinaterna (cos(v), sin(v)), där v som vanligt är motursvinkeln mellan radien och den positiva x-axeln.

För funktionen cos(v) gäller alltså att dess värde är lika med x-koordinaten för en punkt på enhetscirkeln.

Om vinkeln v ligger i intervallet pi/2+n•2pi < v < 3pi/2+n•2pi så är x-koordinaten negativ, dvs funktionsvärdet är mindre än 0.

Om vinkeln v ligger i intervallet -pi/2+n•2pi < v < pi/2+n•2pi så är x-koordinaten positiv, dvs funktionsvärdet är större än 0.

I ett intervall med längd 2pi, säg från v = a till v = a+2pi så kommer de utpekade x-koordinaterna att vara lika mycket positiva som negativa.

Det betyder att de på enhetscirkeln utpekade punkterna kommer att befinna sig lika mycket i vänstra halvplanet (kvadrant 2 och 3) som i högra halvplanet (kvadrant 4 och 1).

Medelvärdet av alla dessa horisontella koordinater kommer att vara 0, vilket innebär att funktiomens medelvärde kommer att vara 0.

== Steg 2: Vi ökar amplituden till 8,6 dvs 8,6cos(v) ==

Vi ändrar nu amplituden från 1 till 8,6. Det motsvarar det att vi utökar cirkelns radie från 1 till 8,6. Det är nu inte längre en enhetscirkel utan en "8,6"-cirkel eftersom varje punkt på denna nya cirkel istället har koordinaterna (8,6cos(v), 8,6sin(v)). Men utöver det så fungerar den på samma sätt som en enhetscirkel.

För funktionen 8,6cos(v) gäller alltså att dess värde är lika med x-koordinaten för en punkt på "8,6"-cirkeln.

Om vinkeln v ligger i intervallet pi/2+n•2pi < v < 3pi/2+n•2pi så är x-koordinaten negativ, dvs funktionsvärdet är mindre än 0.

Om vinkeln v ligger i intervallet -pi/2+n•2pi < v < pi/2+n•2pi så är x-koordinaten positiv, dvs funktionsvärdet är större än 0.

I ett intervall med längd 2pi, säg från v = a till v = a+2pi så kommer de utpekade x-koordinaterna att vara lika mycket positiva som negativa.

Det betyder att de på "8,6"-cirkeln utpekade punkterna kommer att befinna sig lika mycket i vänstra halvplanet (kvadrant 2 och 3) som i högra halvplanet (kvadrant 4 och 1).

Medelvärdet av alla dessa x-koordinater kommer att vara 0, vilket innebär att funktionens medelvärde kommer att vara 0.

== Steg 3: Addera en konstant 8, dvs 8+8,6cos(v) ==

Tänk dig att vi flyttar vår "8,6"-cirkel 8 steg åt höger i vårt koordinatsystem. Vi har då en cirkel med radie 8,6 och medelpunkt i (8, 0).

Vi flyttar även med referenspunkten för vår vinkel v. Vinkeln v är alltså moturs-vinkeln mellan radien och den del av x-axeln som ligger till höger om cirkelns medelpunkt.

För funktionen 8+8,6cos(v) gäller då att dess värde är lika med x-koordinaten för en punkt på vår förskjutna "8,6"-cirkel.

Om vinkeln v ligger i intervallet pi/2+n•2pi < v < 3pi/2+n•2pi så är x-koordinaten mindre än 8, dvs funktionsvärdet är mindre än 8.

Om vinkeln v ligger i intervallet -pi/2+n•2pi < v < pi/2+n•2pi så är x-koordinaten större än 8, dvs funktionsvärdet är större än 8.

I ett intervall med längd 2pi, säg från v = a till v = a+2pi så kommer de utpekade x-koordinaterna att vara lika mycket mindre än 8 som större än 8.

Det betyder att de på "8,6"-cirkeln utpekade punkterna kommer att befinna sig lika mycket till vänster om den vertikala linjen x = 8 som till höger om den.

Medelvärdet av alla dessa x-koordinater kommer att vara 8, vilket innebär att funktionens medelvärde kommer att vara 8.

===============

Det var mycket text att ta in, men gör ett försök, det är bra träning. Rita figurer vid sidan av och koppla dem till texten.

”Jag menar ett intervall vars längd är en multipel av 2pi, ” .. Menar du att det ska vara exempelvis 4pi, 6pi osv? Eller hur menar du med ett intervall vars längd är en multipel av 2pi

Yngve skrev:
Katarina149 skrev:
Hur menar du med ”helt antal perioder” menar du tex 2pi•n , 3pi•n , 4 pi•n…osv? Inte att det exempelvis ska vara 3.5pi•n , 1.2pi•n osv?

Nej, cos(v) har perioden 2pi, så 3pi•n är inte ett helt antal perioder.

Jag menar ett intervall vars längd är en multipel av 2pi, precis som jag skrev tidigare i det här svaret.

___
”Om du vill kan vi göra en illustration med hjälp av enhetscirkeln imorgon.”

Ja jättegärna .

== Steg 1: Funktionen cos(v) och en enhetscirkel ==

Vi ritar ett koordinatsystem där vi kallar den horisontella axeln för x och den vertikala axeln för y.

En radie i enhetscirkeln pekar ut en punkt på cirkeln som har koordinaterna (cos(v), sin(v)), där v som vanligt är motursvinkeln mellan radien och den positiva x-axeln.

För funktionen cos(v) gäller alltså att dess värde är lika med x-koordinaten för en punkt på enhetscirkeln.

Om vinkeln v ligger i intervallet pi/2+n•2pi < v < 3pi/2+n•2pi så är x-koordinaten negativ, dvs funktionsvärdet är mindre än 0.

Om vinkeln v ligger i intervallet -pi/2+n•2pi < v < pi/2+n•2pi så är x-koordinaten positiv, dvs funktionsvärdet är större än 0.

I ett intervall med längd 2pi, säg från v = a till v = a+2pi så kommer de utpekade x-koordinaterna att vara lika mycket positiva som negativa.

Det betyder att de på enhetscirkeln utpekade punkterna kommer att befinna sig lika mycket i vänstra halvplanet (kvadrant 2 och 3) som i högra halvplanet (kvadrant 4 och 1).

Medelvärdet av alla dessa horisontella koordinater kommer att vara 0, vilket innebär att funktiomens medelvärde kommer att vara 0.

== Steg 2: Vi ökar amplituden till 8,6 dvs 8,6cos(v) ==

Vi ändrar nu amplituden från 1 till 8,6. Det motsvarar det att vi utökar cirkelns radie från 1 till 8,6. Det är nu inte längre en enhetscirkel utan en "8,6"-cirkel eftersom varje punkt på denna nya cirkel istället har koordinaterna (8,6cos(v), 8,6sin(v)). Men utöver det så fungerar den på samma sätt som en enhetscirkel.

För funktionen 8,6cos(v) gäller alltså att dess värde är lika med x-koordinaten för en punkt på "8,6"-cirkeln.

Om vinkeln v ligger i intervallet pi/2+n•2pi < v < 3pi/2+n•2pi så är x-koordinaten negativ, dvs funktionsvärdet är mindre än 0.

Om vinkeln v ligger i intervallet -pi/2+n•2pi < v < pi/2+n•2pi så är x-koordinaten positiv, dvs funktionsvärdet är större än 0.

I ett intervall med längd 2pi, säg från v = a till v = a+2pi så kommer de utpekade x-koordinaterna att vara lika mycket positiva som negativa.

Det betyder att de på "8,6"-cirkeln utpekade punkterna kommer att befinna sig lika mycket i vänstra halvplanet (kvadrant 2 och 3) som i högra halvplanet (kvadrant 4 och 1).

Medelvärdet av alla dessa x-koordinater kommer att vara 0, vilket innebär att funktionens medelvärde kommer att vara 0.

== Steg 3: Addera en konstant 8, dvs 8+8,6cos(v) ==

Tänk dig att vi flyttar vår "8,6"-cirkel 8 steg åt höger i vårt koordinatsystem. Vi har då en cirkel med radie 8,6 och medelpunkt i (8, 0).

Vi flyttar även med referenspunkten för vår vinkel v. Vinkeln v är alltså moturs-vinkeln mellan radien och den del av x-axeln som ligger till höger om cirkelns medelpunkt.

För funktionen 8+8,6cos(v) gäller då att dess värde är lika med x-koordinaten för en punkt på vår förskjutna "8,6"-cirkel.

Om vinkeln v ligger i intervallet pi/2+n•2pi < v < 3pi/2+n•2pi så är x-koordinaten mindre än 8, dvs funktionsvärdet är mindre än 8.

Om vinkeln v ligger i intervallet -pi/2+n•2pi < v < pi/2+n•2pi så är x-koordinaten större än 8, dvs funktionsvärdet är större än 8.

I ett intervall med längd 2pi, säg från v = a till v = a+2pi så kommer de utpekade x-koordinaterna att vara lika mycket mindre än 8 som större än 8.

Det betyder att de på "8,6"-cirkeln utpekade punkterna kommer att befinna sig lika mycket till vänster om den vertikala linjen x = 8 som till höger om den.

Medelvärdet av alla dessa x-koordinater kommer att vara 8, vilket innebär att funktionens medelvärde kommer att vara 8.

===============

Det var mycket text att ta in, men gör ett försök, det är bra träning. Rita figurer vid sidan av och koppla dem till texten.

Jag har försökt testa med geogebra också för att förstå hur det ska se ut. Det blev tydligare när jag ritade ett koordinatsystem. Det är lite svårt att hänga med så mycket text utan bilder. Vore bättre om man förklarar mha bilder

Katarina149 skrev:
”Jag menar ett intervall vars längd är en multipel av 2pi, ” .. Menar du att det ska vara exempelvis 4pi, 6pi osv? Eller hur menar du med ett intervall vars längd är en multipel av 2pi

Ja, intervallets längd ska vara exempelvis 0, 2pi, 4pi, 6pi osv.

Katarina149 skrev:

Jag har försökt testa med geogebra också för att förstå hur det ska se ut. Det blev tydligare när jag ritade ett koordinatsystem. Det är lite svårt att hänga med så mycket text utan bilder. Vore bättre om man förklarar mha bilder

Ja, men nu ville jag att du skulle träna på att visualisera på egen hand eftersom många matteuppgifter kräver det, som du har märkt.