Uppgift 2364 i origo 2b

2364 Är det korrekt avskrivet från boken?

rapidos skrev:

2364 Är det korrekt avskrivet från boken?

Ja allt utom Ledtråden det ska stå Ledtråd: Fundera över vilka kombinationer av a och b som ger a upphöjt med b = 1.


här kommer en bild på uppgifterna

Vad får du ut av ledtråden?

Laguna skrev:

Vad får du ut av ledtråden?

Att ända möjligheterna för att svaret ska bli 1 är att antigen basen är 1 eller exponenten är 0. Ända undantaget är att basen kan även vara -1 men då måste exponenten vara jämn. 

Det finns ett fall till, och en knepighet, men du kan börja så. När är exponenten 0?

(Du hittade det extra fallet, ser jag.)

Laguna skrev:

Det finns ett fall till, och en knepighet, men du kan börja så. När är exponenten 0?

För att svarte ska bli 1 så kan inte basen eller exponenten vara vad som helst. Men när exponenten 0 så kan basen vara vad som helst. Eller?

Vad tycker du att 0⁰ är?

Laguna skrev:

Vad tycker du att 0⁰ är?

Ja det går inte eller blir iallfall odefinierat. Men hur början man för att lösa uppgiften?

Vi har ju börjat. När är exponenten 0?

Laguna skrev:

Vi har ju börjat. När är exponenten 0?

Menar du vad x är i exponenten för att få 0. För då är svaret -2 eller 3 får jag fram.

Nästa fall: när är basen 1?

Det är där jag fastnar lite eftersom man inte kan använda pq formel. Försöker att använda kvadratkompletering men fastanar på den och kommer inte vidare

Visst kan du använda pq-formeln om du vill: 

$x^2-5x+5=1$

Flytta över 1:an till VL, alltså subtrahera 1 från VL och HL.

Jaha för när jag försöker lösa den med pq så fpr jag att det är ingen lösning. Det blir negativt under rotenur teknet.

$$\begin{gathered} x^2-5x+5=1 \\ {x}^2-5x+4=0 \\ x=\frac{5}{2}\pm \sqrt{\frac{5}{2}-4} \\ x=2,5\pm \sqrt{2,5-4} \\ x=2,5\pm \sqrt{-1,5} \end{gathered}$$

alvaaaaaaa skrev:

Jaha för när jag försöker lösa den med pq så fpr jag att det är ingen lösning. Det blir negativt under rotenur teknet.

$$\begin{gathered} x^2-5x+5=1 \\ {x}^2-5x+4=0 \\ x=\frac{5}{2}\pm \sqrt{\frac{5}{2}-4} \\ x=2,5\pm \sqrt{2,5-4} \\ x=2,5\pm \sqrt{-1,5} \end{gathered}$$

Jo, jag ser det. Repetera pq-formeln om det behövs.

Så här ser den ut:

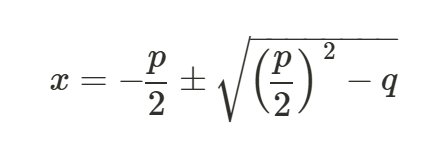
ser nu glömde upphöjt 

Laguna skrev:

Nästa fall: när är basen 1?

Okej nu får jag det till 1 eller 4. Men kan också bli 2 och 3 eftersom att basen kan vara -1 om då exponenten är jämn. 

alvaaaaaaa skrev:

Laguna skrev:

Nästa fall: när är basen 1?

Okej nu får jag det till 1 eller 4. Men kan också bli 2 och 3 eftersom att basen kan vara -1 om då exponenten är jämn. 

Stämmer bra! Så vilka lösningar på ekvationen har du samlat ihop nu?

basen kan vara 1, 4, 2 eller 3 och exponenten -2 eller 3

alvaaaaaaa skrev:

basen kan vara 1, 4, 2 eller 3 och exponenten -2 eller 3

Inte "basen", men x i basen. Samma för "exponenten" ...

Jag fattar vad du menar, men det skadar inte att vara noga.

Jag håller med. Ekvationen har fem lösningar.

exakt det var så jag menade men är det svarte att x kan var de 5 talen eller är det något steg jag missar?

alvaaaaaaa skrev:

exakt det var så jag menade men är det svarte att x kan var de 5 talen eller är det något steg jag missar?

Nejdå. Du missar inget. Bara jag som är lite noga med terminologin.

$x\in \left\{-2; 1;\hspace{0.17em}2;\hspace{0.17em}3;\hspace{0.17em}4\right\}$

Alltså, x tillhör mängden ... (de fem uppräknade talen).