Uppgift 32

Fundera på varför du ska hitta den primitiva funktionen. Vad innebär den primitiva funktionen till accelerationen? När du har listat ut det så blir resten av uppgiften ganska lätt.

Hej! Jag vet att man ska hitta primitiv funktion till a(t) som blir 3t-5e^0,20t. Sen vet jag ej mer 

$a\left(t\right)=3-e^{0.2t}=0$

Tänk att funktionen är förändring i hastighet (acceleration), vad borde då den primitiva funktionen representera?

Mega7853 skrev:

Fundera på varför du ska hitta den primitiva funktionen. Vad innebär den primitiva funktionen till accelerationen? När du har listat ut det så blir resten av uppgiften ganska lätt.

Därför att den primitiva funktionen ger hastigheten till accelerationen då om man derivera en gång till blir det accelerationen. Den primitiva funktionen till accelerationen innebär att hastigheten kan besrämma vid en specifik tidpunkt då accelerationen är lika med noll. 

Affe Jkpg skrev:

Hej! Jag vet att man ska hitta primitiv funktion till a(t) som blir 3t-5e^0,20t. Sen vet jag ej mer 

$a\left(t\right)=3-e^{0.2t}=0$

Ur detta ekvation fick jag ut tiden 2,70805...

Ur detta ekvation fick jag ut tiden 2,70805...

Vad är det som är speciellt med just den tiden?

Ur detta ekvation fick jag ut tiden 2,70805...

$$\begin{gathered} e^{0.2t}=3 \\ 0.2t=\ln \left(3\right) \\ t=... \end{gathered}$$

Affe Jkpg skrev:

Ur detta ekvation fick jag ut tiden 2,70805...

$$\begin{gathered} e^{0.2t}=3 \\ 0.2t=\ln \left(3\right) \\ t=... \end{gathered}$$

Jag fick att tiden är 5, så vi kan integrera från 0 till 5,493061... 

Johannes.C skrev:

Tänk att funktionen är förändring i hastighet (acceleration), vad borde då den primitiva funktionen representera?

Den primitiva funktionen representerar förändring i förflyttningen?

Såhär blev det för mig. 

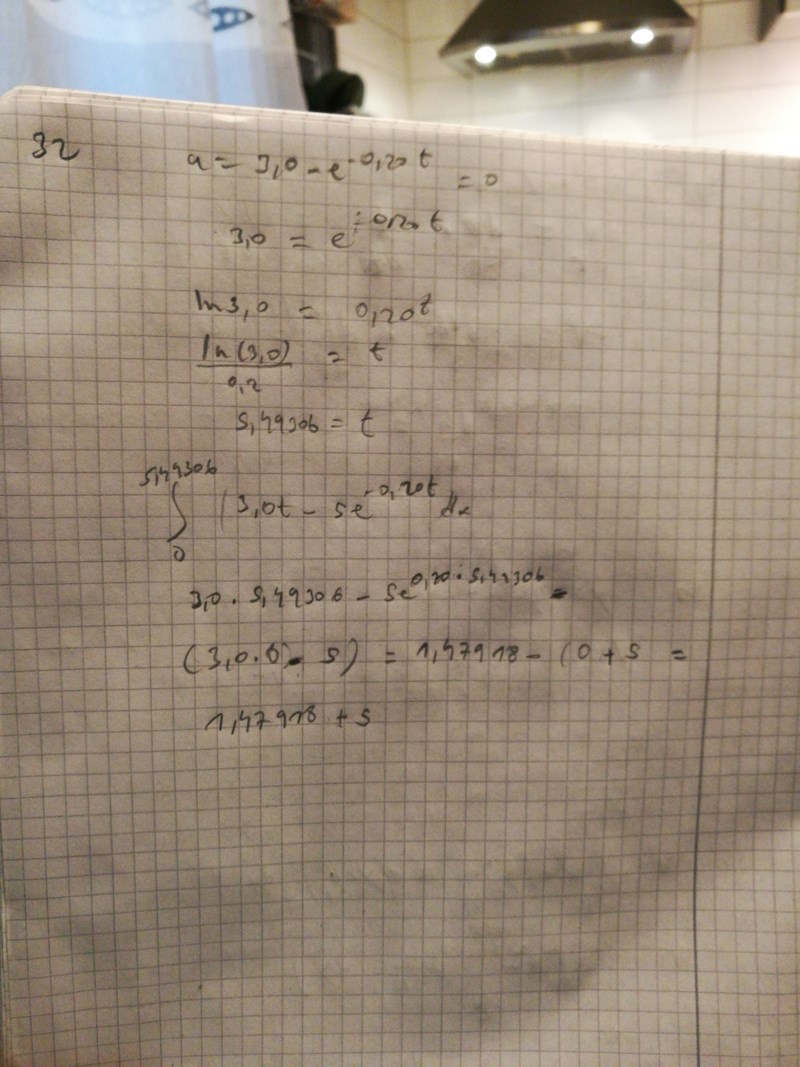
Jag fick att tiden är 5, så vi kan integrera från 0 till 5,493061... 

Jag anar att det finns en poäng med att låta bli decimaltalen och skriva:

t = 5*ln(3)

Glöm nu inte att:
v₀ = 9.5m/s

Affe Jkpg skrev:

Jag fick att tiden är 5, så vi kan integrera från 0 till 5,493061... 

Jag anar att det finns en poäng med att låta bli decimaltalen och skriva:

Vad menar du med 5*ln(3)? 

t = 5*ln(3)

Glöm nu inte att:
v₀ = 9.5m/s

Vad menar du med det? 

Vad menar du med 5*ln(3)? 

$t=\frac{\ln \left(3\right)}{0.2}=5*\ln \left(3\right)$

Vad menar du med det? 

I denna uppgift vid tiden t=0, kan hastigheten skrivas v = v₀ = 9.5 m/s

Ja v =v0+v/2, dock säger facit att den primitiva funktionen är 3,0t-5e^0,20t+14,5

$$\begin{gathered} F\left(t\right)=3t - 5e^{0.2t} + 14.5 \\ F(t=0)=... \end{gathered}$$

Hej! Jag vet att man ska hitta primitiv funktion till a(t) som blir 3t-5e^0,20t.

Det är fel, eftersom du glömde konstanten som brukar skrivas "C"

Affe Jkpg skrev:

$$\begin{gathered} F\left(t\right)=3t - 5e^{0.2t} + 14.5 \\ F(t=0)=... \end{gathered}$$

Hej! Jag vet att man ska hitta primitiv funktion till a(t) som blir 3t-5e^0,20t.

Det är fel, eftersom du glömde konstanten som brukar skrivas "C"

Hur fick du till 14,5 i ekvationen? Jag hänger ej med tyvärr.. 

$$\begin{gathered} a\left(t\right)=f\left(t\right)=3 - e^{0.2t} \\ v\left(t\right)=F\left(t\right)=3t - 5e^{0.2t} +C \\ v(t=0)=F(t=0)=-5+C=9.5 \\ C=14.5 \end{gathered}$$

Du vet att när v t = 0 är partikelns hastighet 9,5 m/s. Använd detta för att räkna ut rätt värde på integrationskonstanten C.

EDIT: rättade felskrivning. Tack Affe!

Du vet att när v = 0 är partikelns hastighet 9,5 m/s

Du vet att när t = 0 är partikelns hastighet 9,5 m/s

Jag gjorde det, men jag får ej hastighetens värde. Dock får jag 86,128554 när jag integrerar från 0 till 5 med primitiva funktionen 3t-5e^0,2t+14,5t 

Visa steg för steg hur du gör när du räknar fram värdet på integrationskonstanten C. 

Jag gjorde det, men jag får ej hastighetens värde. Dock får jag 86,128554 när jag integrerar från 0 till 5 med primitiva funktionen 3t-5e^0,2t+14,5t 

Vadå integrera?

$$\begin{gathered} a\left(t\right)=\frac{dv\left(t\right)}{dt} \\ v\left(t\right)=3t-5e^{0.2t}+14.5 \end{gathered}$$