Uppgift från 2c i gymnasiet

En jämförelse:

Om du får veta att  x + 2y = 3  så är alla punkter på en viss linje lösningar. Vilket x du än väljer så finns det ett y som passar, och alla sådana (x,y) ligger på en rät linje.

Om du sedan får veta att  x - 7y = 12, så får du på samma sätt fram en annan linje. Det enda som stämmer för bägge ekvationerna är (5, -1), där linjerna korsar varandra. Då har du ett ekvationssystem med en lösning.

Men om du hade fått veta att  10x + 20y = 30, så hade du bara fått en ny ekvation för samma linje, och du skulle fortfarande hitta hur många punkter som helst, som ligger på "bägge " linjerna. Då har du ett ekvationssystem med oändligt många lösningar. 

Hej och välkommen till PA!

Som Bubo skriver så betyder "oändligt många lösningar" att båda ekvationerna motsvarar en och samma linje.

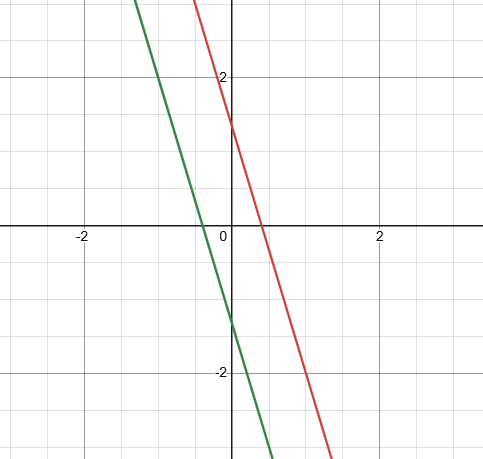
Så här ser det ut om A=0 och B=0. Vi har en enda lösning, där linjerna skär varandra:

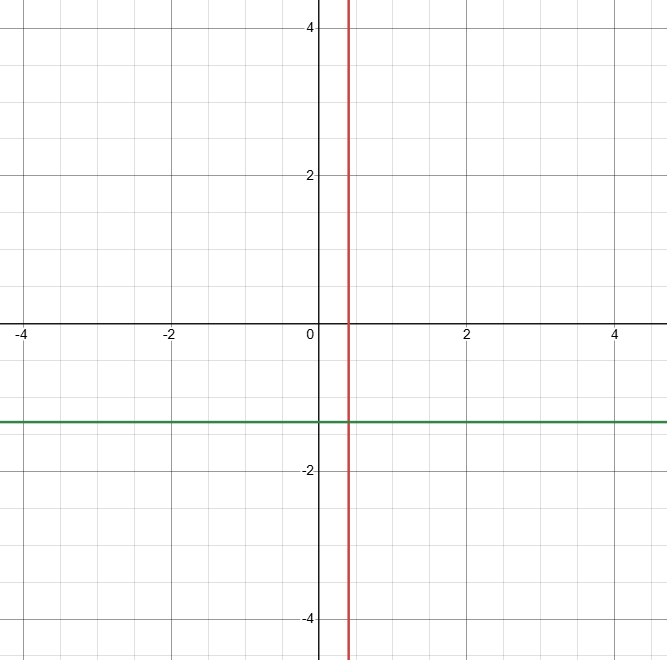
När A=-10 och B=4,5 så skär linjerna aldrig varandra och då saknas lösningar.

Vi skriver ut två ekvationerna för två linjer:

$\left\{\begin{array}{l}y=k_{1}x+m_1\\ y=k_{2}x+m_2\end{array}\right.$

För att ekvationssystemet skall ha oändligt många lösningar, så måste k₁=k₂ och m₁=m₂.

Första steget för att lösa din uppgift är att skriva om ekvationerna på formen y=kx+m. Det är inte jättelätt, men försök gärna.

När du kommit så långt är det dags att räkna ut vad A och B skall vara. 

Det är enklast att börja med m-värdet för att få ut B:

Kommer du vidare härifrån?

Ja, tack så mycket❤️