Uppgift om elektriska kretsar
Hur löser man uppgift B? Sättet jag tänker är att det sker som två seperata kretsar, där det finns 2 olika "strömmar" genom CB som kommer ha två olika riktningar, men det verkar inte riktigt vara så man ska göra enligt facit?
Tänker på detta vis då jag antar att elektroner vill ta vägen med minst resistans, vilket då blir vägen med minst resistorer i detta fall? Så att det skapas en ström av 1A (3V/3Ω) i kretsen med 2 batterier och en ström av 0,25 A i kretsen med ett batteri (1,5V/6Ω)
Hej,
Det är lite farligt att tänka att strömmen tar enklaste vägen, och samtidigt tänka att det bara finns en väg som är enklast. I det här fallet fungerar det eftersom det finns ingen enklare väg för strömmen att ta, än genom en kortslutning. I andra fall kan det vara ganska svårt att meddetsamma se vad som är enklaste vägen.
Har ni gått igenom potentialvandring, och kirchoffs lagar?
JohanF skrev:Hej,
Det är lite farligt att tänka att strömmen tar enklaste vägen, och samtidigt tänka att det bara finns en väg som är enklast. I det här fallet fungerar det eftersom det finns ingen enklare väg för strömmen att ta, än genom en kortslutning. I andra fall kan det vara ganska svårt att meddetsamma se vad som är enklaste vägen.
Har ni gått igenom potentialvandring, och kirchoffs lagar?
Vi gick precis igenom de!
Vad bra! Med dem så kommer du att se vilka vägar strömmarna tycker är enklaste vägen, och hur stor den elektriska potentialen är i varje punkt.
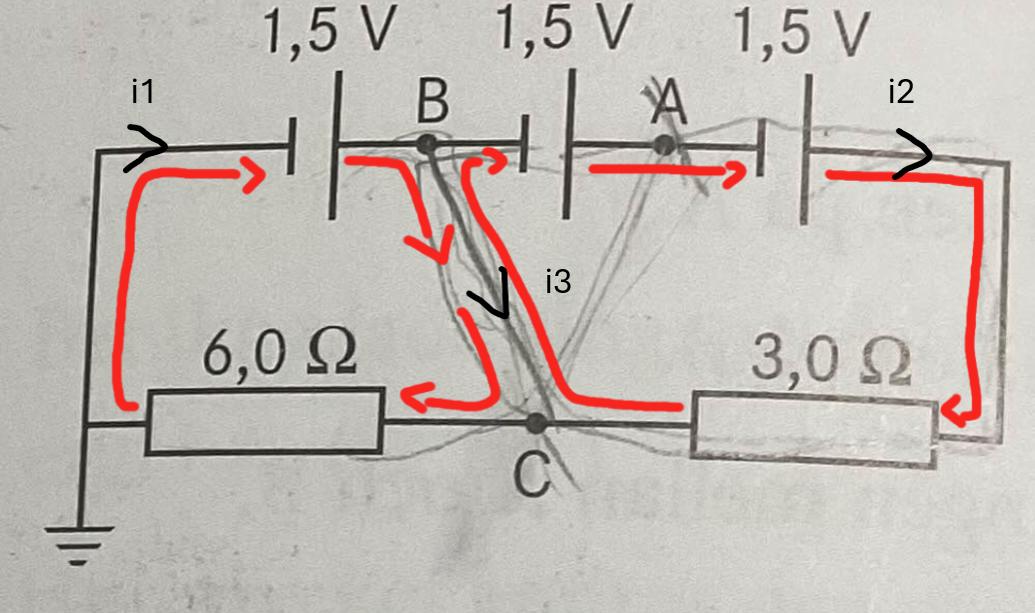
Kommer du ihåg hur man gör? Jag har satt ut de tre olika strömmarna i1, i2 och i3, som flyter i kretsen. Kan du potentialvandra?
JohanF skrev:Vad bra! Med dem så kommer du att se vilka vägar strömmarna tycker är enklaste vägen, och hur stor den elektriska potentialen är i varje punkt.
Kommer du ihåg hur man gör? Jag har satt ut de tre olika strömmarna i1, i2 och i3, som flyter i kretsen. Kan du potentialvandra?
Blir det alltså så att man får pröva alla möjliga vägar för strömmen?
i1 har då strömmen 0.5 A, i2 har 1 A, i3 har 0.25 A? Kommer i2 på något sätt ta ut i3 då de går emot varandra i kortslutningen?
Man behöver inte prova alla möjliga vägar, utan man ställer upp de elektriska samband som måste gälla. Och på så sätt får man fram alla strömmar och spänningar.
1. Summan av alla strömmar in i en nod, måste vara noll.
2. Summan av samtliga potentialfall i varje sluten strömkrets är noll.
Potentialvandrar du i vänstra delkretsen så får du
1.5-6*i1=0 => i1=0.25A
Potentialvandrar du i högra delkretsen så får du
1.5+1.5-3*i2=0 => i2=1A
Hur stor måste då i3 vara om strömmarna ska uppfylla samband 1?
JohanF skrev:Man behöver inte prova alla möjliga vägar, utan man ställer upp de elektriska samband som måste gälla. Och på så sätt får man fram alla strömmar och spänningar.
1. Summan av alla strömmar in i en nod, måste vara noll.
2. Summan av samtliga potentialfall i varje sluten strömkrets är noll.
Potentialvandrar du i vänstra delkretsen så får du
1.5-6*i1=0 => i1=0.25A
Potentialvandrar du i högra delkretsen så får du
1.5+1.5-3*i2=0 => i2=1A
Hur stor måste då i3 vara om strömmarna ska uppfylla samband 1?
Verkar som vi bara gått igenom andra lagen och inte den första om noderna, men nu förstår jag att i3 måste vara 0.75 för att i3+i1=i2. Verkar ändå väldigt logiskt!
Tack för hjälpen!
Bra! Visst är det härligt när pusselbitarna faller på plats?
I vilken riktning går I3? Uppåt eller neråt i figuren?
JohanF skrev:Bra! Visst är det härligt när pusselbitarna faller på plats?
I vilken riktning går I3? Uppåt eller neråt i figuren?
Tänker att den går upp!
Det tänker du alldeles rätt i!
