Uppgiftsbank-Matematik 3-Derivata

Nivå: E

Uppgift: Den vägsträcka $s\left(t\right)$ meter som en bil har rört sig på tiden $t$ sekunder ges av sambandet $s\left(t\right)=2t+4t^2$. Beräkna och tolka med ord.

a) $s\left(5\right)$

b) $s\text{'}\left(5\right)$

Lösning: 

a) $s\left(5\right)=2·5+4·5^2=10+100=110$m , Svar: Bilen har rört sig en sträcka av 110 meter på 5 sekunder.

b) $s\text{'}\left(t\right)=2+8t\Rightarrow s\text{'}\left(5\right)=2+8·5=2+40=42$ m/s, Svar: Bilen har en hastighet på 42 m/s vid 5 sekunder.

Skriven av: Jonis10

Nivå: E

Uppgift: Bestäm ekvationen för tangenten till funktionen $f\left(x\right)=x^4-4x$ i punkten $(2,8)$.

Lösning: $f\text{'}\left(x\right)=4x^3-4\Rightarrow f\text{'}\left(2\right)=4·2^3-4=28$, tangenten kan skrivas på formen $y=kx+m$ där $k=f\text{'}\left(2\right)=28$ vilket ger $y=28x+m$.

Vi vet också att linjen går igenom punkten $(2,8)$ vilket ger $y\left(2\right)=8\iff 8=28·2+m\iff m=-48$

Svar: $y=28x-48$

Skriven av: Jonis10

Nivå: E

Uppgift: Bestäm $f\text{'}\left(x\right)$ om

a) $f\left(x\right)=4x^3+8x^2$

b) $f\left(x\right)=4x$

c) $f\left(x\right)=9$

Lösning: 

a) $f\text{'}\left(x\right)=4·3x^{3-1}+8·2x^{2-1}=12x^2+16x$ , Svar: $f\text{'}\left(x\right)=12x^2+16x$

b) $f\left(x\right)=4x=4x^1\Rightarrow f\text{'}\left(x\right)=4·1·x^{1-1}=4x^0=4·1=4$, Svar: $f\text{'}\left(x\right)=4$

c) Derivatan av en konstant är alltid noll $f\left(x\right)=9\Rightarrow f\text{'}\left(x\right)=0$, Svar: $f\text{'}\left(x\right)=0$

Skriven av: Jonis10

Nivå: E

Uppgift: Grafen till $h\left(x\right)=3x^3-9x$ har en maximipunkt. Bestäm maximipunktens koordinater.

Lösning: $h\text{'}\left(x\right)=9x^2-9$, en egenskap som gäller för en extrempunkt det är att lutningen är noll dvs $h\text{'}\left(x\right)=0\iff 9x^2-9=0\iff x^2=1\iff x=\pm 1\iff x_1=1 , x_2=-1$.

$h\text{'}\text{'}\left(x\right)=18x\Rightarrow h\text{'}\text{'}\left(1\right)=18·1=18$, eftersom $h\text{'}\text{'}\left(1\right)>0$ är det en minimipunkt.

$h\text{'}\text{'}(-1)=18·(-1)=-18$, eftersom $h\text{'}\text{'}(-1)<0$ är det en maximipunkt.

$h(-1)=3·(-1{)}^3-9·(-1)=-3+9=6$

Svar: $(-1,6)$

Skriven av: Jonis10

Nivå: E

Uppgift: Bestäm med hjälp av derivata rektangelns maximala area.

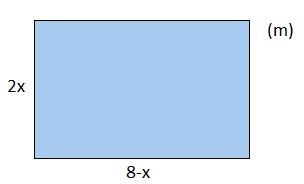
Lösning: Arean för en rektangel är det samma som: $A=bh$, där $b$ är basen och $h$ är höjden.

Eftersom arean beror av variabeln $x$ kan vi ska en funktion som beskriver arean för rektangeln.

$A\left(x\right)=(8-x)2x=16x-2x^2\Rightarrow A\text{'}\left(x\right)=16-4x\Rightarrow A\text{'}\text{'}\left(x\right)=-4$

$A\text{'}\left(x\right)=0\iff 16-4x=0\iff x=4$, $A\text{'}\text{'}\left(4\right)=-4\Rightarrow A\text{'}\text{'}\left(4\right)<0$ det är en maximipunkt.

$A\left(4\right)=(8-4)·2·4=4·2·4=32 {\mathrm{m}}^2$

Svar: $32 {\mathrm{m}}^2$

Skriven av: Jonis10 

Nivå: C

Uppgift: Bestäm den funktion $g\left(x\right)=k{x}^3+k{x}^2$ där $k$ är en konstant, för vilken det gäller att $g\text{'}\left(2\right)=2$.

Lösning: $g\text{'}\left(x\right)=3k{x}^2+2kx=k(3x^2+2x)$, eftersom: $g\text{'}\left(2\right)=2\iff 2=k(3·2^2+2·2)\iff k=\frac{2}{(3·2^2+2·2)}=\frac{2}{16}=\frac{1}{8}$

Svar: $g\left(x\right)=\frac{x^3}{8}+\frac{x^2}{8}$

Skriven av: Jonis10

Nivå: C

Uppgift: Två tangenter till $y=x^2-3x+2$ skär varandra i en punkt och tangenterna tangerar kurvan då $x=-2$ och då $x=1$. Bestäm skärningspunktens koordinater.

Lösning: $y\text{'}=2x-3$

Tangenten då $x=-2$:

$y(-2)=(-2{)}^2-3·(-2)+2=4+6+2=12$

 $y\text{'}(-2)=2·(-2)-3=-4-3=-7$

Vilket ger linjen: $12=-2·(-7)+m_1\iff m_1=-2$, $y_1=-7x-2$

Tangenten då $x=1$:

$y\left(1\right)=1^2-3·1+2=1-3+2=0$

$y\text{'}\left(1\right)=2·1-3=2-3=-1$

Vilket ger linjen: $0=-1·1+m_2\iff m_2=1$, $y_2=-x+1$

$y_1=y_2\iff -7x-2=-x+1\iff -3=6x\iff x=-\frac{1}{2}$

$y_2(-\frac{1}{2})=-\left(-\frac{1}{2}\right)+1=\frac{3}{2}$

Svar: $(-\frac{1}{2},\frac{3}{2})$

Skriven av: Jonis10

Nivå: C

Uppgift: Bestäm $f\text{'}\left(9\right)$ då $f\left(x\right)=6\sqrt{x}-\frac{x^2}{2}$

Lösning: $f\left(x\right)=6x^{\frac{1}{2}}-\frac{x^2}{2}\Rightarrow f\text{'}\left(x\right)=6·\frac{1}{2}{x}^{{}^{\frac{1}{2}-1}}-\frac{2x^{2-1}}{2}=3x^{-\frac{1}{2}}-x=\frac{3}{\sqrt{x}}-x$

$f\text{'}\left(9\right)=\frac{3}{\sqrt{9}}-9=\frac{3}{3}-9=1-9=-8$

Svar: $f\text{'}\left(9\right)=-8$

Skriven av: Jonis10

Nivå: C

Uppgift: Kapitalet på Yngves bankkonto växer enligt $K\left(x\right)=12000e^{0,018x}$, där $K\left(x\right)$ är värdet i kronor efter $x$ år.

a) Hur stor är räntesatsen?

b) Beräkna $K\text{'}\left(4\right)$ och förklara innebörden av din beräkning.

Lösning: 

a) I detta fallet frågas det efter förändringsfaktor vilket lika med $e^{0,018}\approx 1.018$ dvs en räntesats på$100\left(1-1.018\right)=1,8\%$ , Svar: 1,8%.

b) $K\text{'}\left(x\right)=0,018·12000e^{0,018x}=216e^{0,018x}\Rightarrow K\text{'}\left(4\right)=216e^{0,018·4}\approx 232$ kr/år

Svar: Efter 5 år ökar/växer Yngves pengar med 232 kr/år.

Nivå: C

Uppgift: Bestäm största och minsta värdet för $f\left(x\right)$ då: $f\left(x\right)=x^3+3x^2-24x+15$, $0\le x\le 4$

Lösning:

 $$\begin{gathered} f\text{'}\left(x\right)=3x^2+6x-24\Rightarrow f\text{'}\left(x\right)=0\iff 3x^2+6x-24=0\iff x^2+2x-8=0 \\ \iff x=-1\pm 3\iff x_1=2 , \left(x_2=-4\right) \end{gathered}$$

$x_2$ lösningen är inte intressant eftersom vi undersöker i intervallet $0\le x\le 4$

$f\text{'}\text{'}\left(x\right)=6x+6\Rightarrow f\text{'}\text{'}\left(2\right)=6·2+6=18\Rightarrow f\text{'}\text{'}\left(2\right)>0$, vilket säger att det är en minimipunkt. 

$f\left(2\right)=2^3+3·2^2-24·2+15=-13$

Vi måste även undersöka ändpunkterna på intervallet vilket ger:

$$\begin{gathered} f\left(0\right)=0^3+3·0^2-24·0+15=15 \\ f\left(4\right)=4^3+3·4^2-24·4+15=31 \end{gathered}$$

Svar: Största värdet: 31 , Minsta värdet: -13

Skriven av: Jonis10

Nivå: A

Uppgift: Funktionen $t$ uppfyller följande två villkor $t\left(4\right)=6$ och $-1\le t\text{'}\left(x\right)\le 2$. Vilka värden kan $t\left(8\right)$ anta?

Lösning: Då $t\text{'}\left(x\right)=-1\Rightarrow y_1=-x+m_1$ och går igenom punkten $(4,6)$ det ger: $y_1\left(4\right)=6\iff 6=-4+m_1\iff m_1=10\Rightarrow y_1=-x+10\Rightarrow y_1\left(8\right)=-8+10=2$

Då $t\text{'}\left(x\right)=2\Rightarrow y_2=2x+m_2$ och går igenom punkten $(4,6)$ det ger: $y_2\left(4\right)=6\iff 6=2·4+m_2\iff m_2=-2\Rightarrow y_2=2x-2\Rightarrow y_2\left(8\right)=2·8-2=14$

Svar: $2\le t\left(8\right)\le 14$

Skriven av: Jonis10

Nivå: A

Uppgift: Visa med hjälp av derivatans definition vad derivatan till $f\left(x\right)=\frac{1}{x}$ blir.

Lösning:

 $$\begin{gathered} f\text{'}\left(x\right)=\underset{h\to 0}{\lim }\frac{f(x+h)-f\left(x\right)}{h}=\underset{h\to 0}{\lim }\frac{1}{h}\left(\frac{1}{(x+h)}-\frac{1}{x}\right)=\underset{h\to 0}{\lim }\frac{1}{h}\left(\frac{x}{x(x+h)}-\frac{(x+h)}{x(x+h)}\right) \\ =\underset{h\to 0}{\lim }\frac{1}{h}\left(\frac{x-(x+h)}{x(x+h)}\right)=\underset{h\to 0}{\lim }\frac{1}{\cancel{h}}·\frac{-\cancel{h}}{x(x+h)}=\underset{h\to 0}{\lim }-\frac{1}{x(x+h)}=-\frac{1}{x^2} \end{gathered}$$

Svar: $f\text{'}\left(x\right)=-\frac{1}{x^2}$

Skriven av: Jonis10

Nivå: A

Uppgift: Visa algebraiskt att $4x^6-8x^3\ge -4$

Lösning: Om t.ex. $f\left(x\right)=4x^6-8x^3$ så blir olikheten $f\left(x\right)\ge -4$. För att kunna visa det behöver vi ta fram det minsta värdet funktionen $f\left(x\right)$ kan anta.

$f\text{'}\left(x\right)=24x^5-24x^2=24x^2(x^3-1)$ , $f\text{'}\left(x\right)=0\iff 24x^2(x^3-1)=0\iff x_1=0 , x_2=1$

$f\text{'}\text{'}\left(x\right)=120x^4-48x$, då $x=1\Rightarrow f\text{'}\text{'}\left(1\right)=120·1^4-48·1=72\Rightarrow f\text{'}\text{'}\left(1\right)>0$ vilket säger att det är en minimipunkt.

Vilket ger att det minsta värdet funktionen $f\left(x\right)$ kan anta är $f\left(1\right)=4·1^6-8·1^3=4-8=-4$. Vilket gör att $f\left(x\right)\ge -4 \mathrm{V}.\mathrm{S}.\mathrm{V}$

Skriven av: Jonis10

Nivå: A

Uppgift: Bestäm $t\text{'}\left(100\right)$ då $t(x+h)=t\left(x\right)+h$

Lösning: $t\text{'}\left(x\right)=\underset{h\to 0}{\lim }\frac{t(x+h)-t\left(x\right)}{h}=\underset{h\to 0}{\lim }\frac{t\left(x\right)+h-t\left(x\right)}{h}=\underset{h\to 0}{\lim }\frac{h}{h}=1$, eftersom $t\text{'}\left(x\right)=1$ för alla $x$ så medför det att $t\text{'}\left(100\right)=1$

Svar: $t\text{'}\left(100\right)=1$

Skriven av: Jonis10

Nivå: A

Uppgift: En skål har formen av en rak cirkulär cylinder. Basytans radie och cylinderns höjd ska tillsammans ha längden 50 cm. Vilka dimensioner ska skålen ha för att få maximal volym?

Lösning: Om vi kallar radien för $r$ och höjden för $h$ ger det oss att: $r+h=50\iff h=50-r (r,h>0)$. 

Volymen för en cirkulär cylinder är: $V=Ah=r^2\mathrm{\pi }h\Rightarrow V\left(r\right)=r^2\mathrm{\pi }(50-r)=50r^2\mathrm{\pi }-\mathrm{\pi }{r}^3\Rightarrow V\text{'}\left(r\right)=100r\mathrm{\pi }-3\mathrm{\pi }{r}^2$

$V\text{'}\left(r\right)=0\iff 100r\mathrm{\pi }-3\mathrm{\pi }{r}^2=0\iff r\mathrm{\pi }(100-3r)=0\iff \left(r_1=0\right), r_2=\frac{100}{3}\approx 33 \mathrm{cm}$

$V\text{'}\text{'}\left(r\right)=100\mathrm{\pi }-6\mathrm{\pi }r\Rightarrow V\text{'}\text{'}\left(\frac{100}{3}\right)=100\mathrm{\pi }-6\mathrm{\pi }·\frac{100}{3}=-100\mathrm{\pi }\Rightarrow V\text{'}\text{'}\left(\frac{100}{3}\right)<0$ vilket säger att det är en maximipunkt. Då $r=\frac{100}{3}\Rightarrow h=50-\frac{100}{3}=\frac{150-100}{3}=\frac{50}{3}\approx 17 \mathrm{cm}$

Svar: Då höjden är 17 cm och radien 33 cm

Skriven av: Jonis10

Kan denna uppgiftsbank uppdateras? Jätte användbart!

Iridiumjon skrev:

Kan denna uppgiftsbank uppdateras? Jätte användbart!

Håller med