Utbredda laster

Jag ska räkna ut tvärkraften, V(x), och momentfördelningen, M(x), i en balk som är fast inspänd vid o.

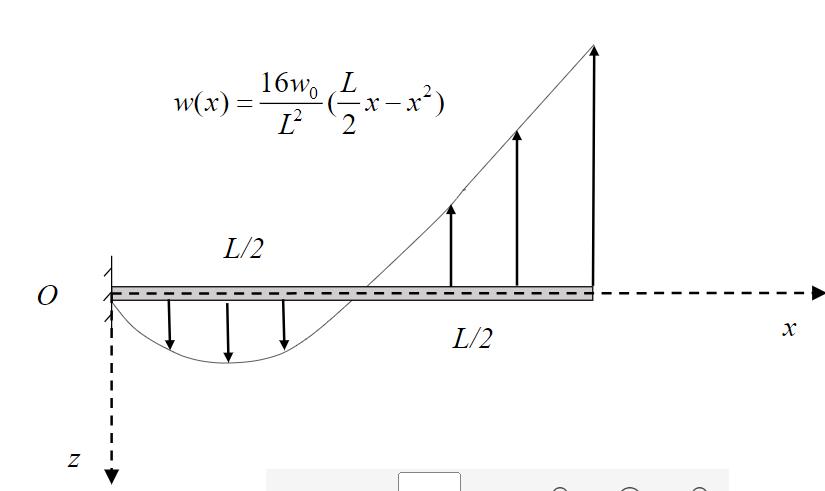
Jag frilägger:

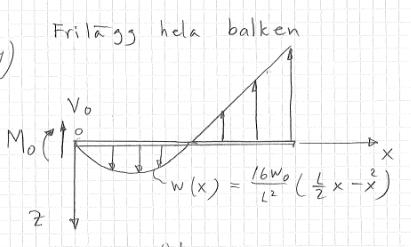
Och ställer upp jämvikts ekvationer: x- led: $- v_{0} + \int_{0}^{\frac{L}{2}} w (x) d x - \int_{\frac{L}{2}}^{L} w (x) d x = 0$

En moment punkt vid o ger: $- M_{0} - \int_{0}^{\frac{L}{2}} x w (x) d x + \int_{\frac{L}{2}}^{L} x w (x) d x = 0$

Nu när jag ska lösa ut $v_{0}$ blir det fel, jag får $2 w_{0} L$ när det ska bli $- \frac{4}{3} w_{0} L$ . Vad gör jag för fel?

I plotten av w(x) i din första figur ser du att den blir negativ efter L/2. När du sedan tar integralerna separat med olika tecken får du samma riktning på krafterna i båda delarna. Det ger ett för högt värde.

Funktionen w(x) är med andra ord kontinuerlig längst hela balken och du behöver ej dela upp den på det sättet.

skye skrev:
I plotten av w(x) i din första figur ser du att den blir negativ efter L/2. När du sedan tar integralerna separat med olika tecken får du samma riktning på krafterna i båda delarna. Det ger ett för högt värde.

Funktionen w(x) är med andra ord kontinuerlig längst hela balken och du behöver ej dela upp den på det sättet.

Tack så mycket!

När du har lastintensiteten beskriven på det här sättet använder man normalt elastiska linjens ekvation:

$q\left(x\right)=-\dfrac{d}{dx}V\left(x\right)$

$V\left(x\right)= \dfrac{d}{dx}M\left(x\right)$

Svara

Visa senaste svar