Utesluta negativ lösning

Svaret man får på denna uppgift förvirrar mig

Min lösning

$a\times \sin \left(x\right) + b\times \cos \left(x\right) = \sqrt{a^2+b^2}\times \sin (x+{\tan }^{-1}(\frac{b}{a}\left)\right)$
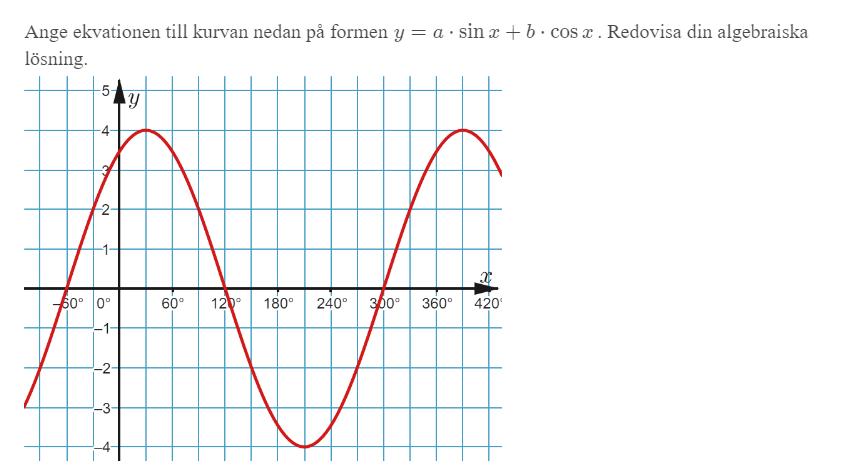
Vi ser i figuren att f(x) går mellan -4 och 4. Det innebär att koefficienten framför är 4 (kan inte vara -4 pga rot)
$\sqrt{a^2+b^2 }=4$
$a^2+b^2=16$

Sedan ser vi att funktionen är förtjuten 60 grader åt vänster då en sinusfunktion vanligt vis är 0 vid x = 0, i denne är den det vid $-60°$. Addition flyttar den åt vänster => ${\tan }^{-1}\left(\frac{b}{a}\right)=60°$
$\frac{b}{a}=\tan (60°)=\sqrt{3}$

Då får vi ekvationssystemet

$a^2+b^2=16$
$\frac{b}{a}=\sqrt{3}$

Vi får att $b = a\sqrt{3}$
$a^2+{\left(a\sqrt{3}\right)}^2=a^2+3a^2=4a^2=16$
$a^2=4$
$a=\pm 2$
$b=\pm 2\sqrt{3}=\pm \sqrt{12}$

Det som blir problematiskt då är att om a = -2 är b = -sqrt(12) vilket om man lägger den tillbaka i den ursprungliga funktionen $a\sin \left(x\right) + b\cos \left(x\right)$ så är denna "lösning" = -f(x), men om man lägger in den i den andra varianten med endast sinx så stämmer den eftersom att de negativa värdena försvinner i kvadreringen och divisionen. I detta fall vet jag vilken som är den korrekta lösningen, men det stör mig att jag får en felaktig lösning på köpet och i fall kanske det skulle vara svårare att urskilja den korrekta lösningen. Finns det något sätt att undvika detta?