Uttryck 2275

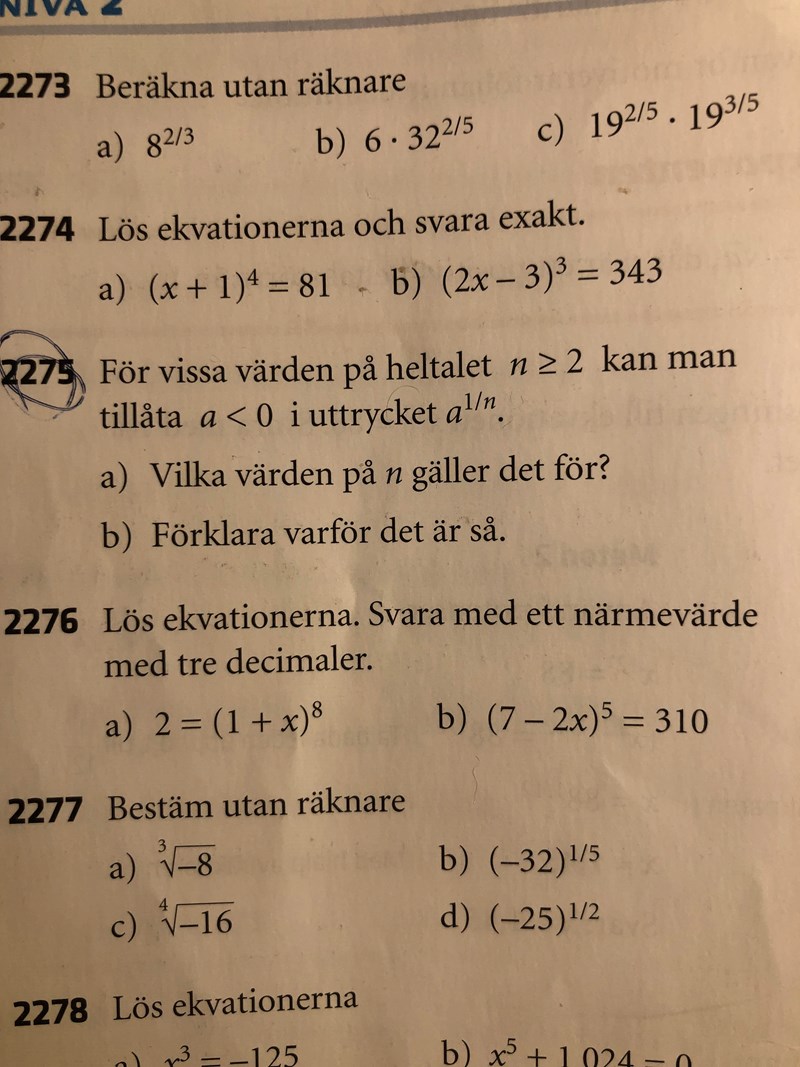
Vad händer om n är jämnt och a<0?

om n är jämnt. Vi säger att n är 4

och a är -0,8

då blir det :   ${(-0·8)}^{\frac{1}{4} }= -0,9457$

Jag ser inget mönster. 

Om jag testar med andra siffror :

${(-3)}^{\frac{1}{3}}=-1.4422....$

Hur kan man istället tänka?

Blir vänsterledet positivt eller negativt? Blir högerledet positivt eller negativt?

Smaragdalena skrev:

Blir vänsterledet positivt eller negativt? Blir högerledet positivt eller negativt?

VL=HL 

om högerleden är negativ så är vänsterleden också negativ. 

Vi väljer ett negativt värde, t ex -3 till a och ett jämnt tal, t ex 2 som n. Då blir (-3)^1/2 lika med $\sqrt{-3}$. Funkar det?

nej man kan inte ta roten ur ett negativt tal

Renny19900 skrev:

nej man kan inte ta roten ur ett negativt tal

Exakt. Kvadraten av ett tal är alltid ett positivt tal, både om talet är positivt och om talet är negativt.

Hur är det med kuben på ett tal, d v s x³? Kan en kub av ett reellt tal vara negativ?

Nej för man kan inte ta kvadratroten ur x^3, man ska ta tredje roten ur x^3 . Förstår fortfarande inte vilken slutsats jag kan dra

Kan du dra tredje roten ur ett negativt tal?

Jo, det kan man... Man kan ta tredje roten ur ett negativt tal... Exempelvis (-125)^(1/3)= -5

okej hittills har jag förstått att talet ” a” kan vara vilket tal som helst som är mindre än 0, exempelvis (-2) eller (-4)

a^1/n ska vara ett heltal. 

Vi säger att a=(-3) 

n ska vara större än 2. 
om n är 3 

Blir uttrycket 

(-3)^(1/3) = (-1,4422..) -> det är inget heltal... 
Ska man bara testa sig fram tills man hittar ett värde på n som ger ett heltal? Tänker jag rätt eller fel? Hur ska man annars tänka? 

Tack för all hjälp! Det uppskattas!

a^1/n ska vara ett heltal.

Nej, så står det inte. Det står att för vissa värden på heltalet n funkar det även om a är ett negativt tal. Detta fungerar om n är ett udda tal, men inte om n är ett jämnt tal. Det går att dra n-te roten ur ett negativt tal om n är ett negativt tal, men inte om n är ett jämnt tal. Eftersom n är ett heltal så är n antingen jämnt eller udda, inte något annat.

jaha alltså är det n som ska vara ett heltal inte hela uttrycket. 

”vilka värden på n gäller det för”? 
N kan vara 3,4,5,6...osv > 2

vad är det man ska räkna ut på uppgift A)?

Nej, n (inte N) skall vara ett udda tal. Vilka tal är det som är udda?

Det man skall räkna ut i uppgift a) är att det fungerar för udda n, men inte för jämna n.

Jag förstår fortfarande inte frågan..... Vad det är man ska räkna ut.. Varför ska n vara udda? Förstår inte det. 

Skulle uppskatta om ni kunde förklara :)

Är du med på att:

$$\begin{gathered} a^{1/2}=\sqrt[]{a} \\ {a}^{1/3}=\sqrt[3]{a} \end{gathered}$$

Är du med på vad $\sqrt[3]{a}$betyder?

Jo nu tror jag att jag förstår.

talet a är negativt 

en negativ bas går inte att upphöjas till en positiv exponent. Vilket innebär att n måste vara ett udda tal. Stämmer det?

Renny19900 skrev:

Jo nu tror jag att jag förstår.

talet a är negativt 

en negativ bas går inte att upphöjas till en positiv exponent. Vilket innebär att n måste vara ett udda tal. Stämmer det?

En negativ bas, t.ex. -5 går visst att upphöja till en positiv exponent, t.ex. 3. Skrev du vad du menade här?

En jämn exponent menar jag :) Tack, märkte nyss att ett positivt tal inte är samma sak som ett jämnt tal 

Det går alldeles utmärkt att upphöja en negativ bas till en jämn exponent, exempelvis är (-2)⁴=16.

Läs igenom frågan igen - den handlar om något helt annat än aⁿ.

Man kan inte upphöja (-2)^1/4 men (-2)^4 kan man upphöja till.  

Men däremot kan man upphöja (-2)^1/3