Uttryck för kinetisk energi, dynamik

Hej! Jag har jobbat med den här uppgiften länge och behöver nu lite hjälp att reda ut uttrycket för kinetisk energi. Min tanke är att energin bevaras i systemet, och genom att ställa upp ett uttryck för den totala energin E och sedan derivera uttrycket ( $\frac{d E}{d t} = 0$ eftersom energin bevaras) kommer jag få en differentialekvation, från vilken jag kan härleda ett uttryck för systemet frekvens (och tillslut periodtid).

Den potentiella energin får jag till $V = \frac{4}{3 π} R (1 - \cos θ)$ , men jag fastnar på uttrycket för kinetisk energi. Jag tänker att alla punkter i cylindern, inklusive G, roterar kring O men att O rör sig rakt i sidled. Jag ser två sätt att tänka på:

Använda att T = $\frac{1}{2} I_{O} \dot{θ^{2}}$ , problemet jag ser här är att O inte är en fix punkt och att man därför även måste ta hänsyn till O:s rörelse på något sätt.
Använda att T = energin från rotationshastighet kring masscentrum + energin från masscentrums translationshastighet = $\frac{1}{2} I_{G} ω^{2} + \frac{1}{2} m v_{G}^{2}$ , där I är tröghetsmomentet och $ω$ är rotationshastighet kring masscentrum. Problemet jag ser här är att jag tänker att det inte finns någon rotation kring masscentrum, alla punkter i cylindern roterar ju tillsammans med G runt O. Det gör att vi endast tar med masscentrums translationshastighet i den kinetiska energin, men förlorar vi inte det bidrag till energin som kommer från att cylindern faktiskt roterar då?

Det hade varit trevligt att använda formeln T = $\frac{1}{2} I_{G} ω^{2} + \frac{1}{2} m v_{G}^{2}$ för punkten O istället för G, men denna formel är ju framtagen under förutsättningen att hastigheterna gäller för G, inte en annan punkt O (om det skulle tas fram en formel kring en annan punkt än G skulle det tillkomma termer i formeln, så som jag förstått det).

Väldigt tacksam för hjälp!

Detta är från vad jag förstår Meriam & Kraige Engineering Mechanics, utgåva 7?

Varför vill du derivera total energi? I avsnitt 8.4 ska man ställa upp rörelseekvationen för systemet från vilken den naturliga frekvensen kan hämtas. Om du vill använda energi skulle jag likställa maximal potentiell energi i ett ändläge med maximal kinetisk energi i mittenläget (eftersom det är harmonisk svängning).

Följer man avsnittet uppgiften tillhör frilägger vi en godtycklig punkt och använder tillhörande rörelseekvation:

$\sum_{}^{} M_{O} = I_{O} \overset{. .}{θ}$

Problemet med denna uppgift är att vår kropp inte rör sig kring punkten som designerats O utan den kan betraktas som rörande kring en punkt C vid nedersidan. Om vi frilägger kroppen vid en godtycklig vinkel $θ$ :

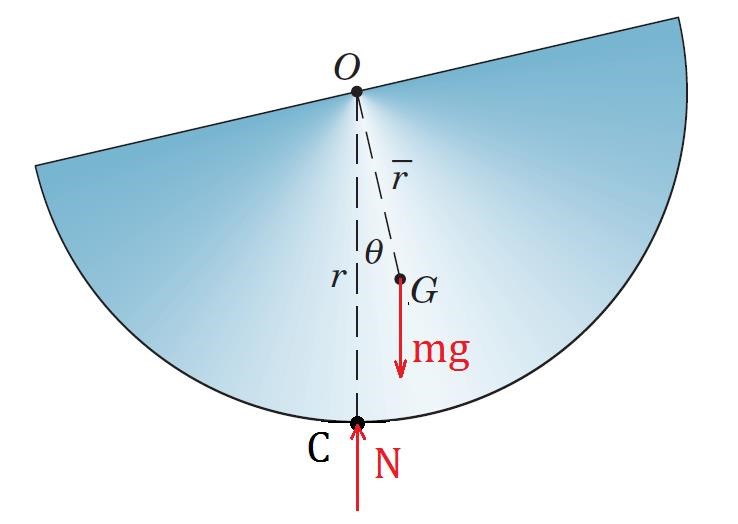
Vi har nu följande rörelseekvation:

$- m g \bar{r} \sin (θ) = I_{C} \overset{. .}{θ}$

Masströghetsmomentet kring punkten C är:

$I_{C} = I_{G} + m (R - \bar{r})^{2} = I_{G} + m R^{2} - 2 m R \bar{r} + m {\bar{r}}^{2} I_{O} = I_{G} + m {\bar{r}}^{2} I_{C} = I_{O} + m R^{2} - 2 m R \bar{r} = m R^{2} (\frac{3}{2} - \frac{8}{3 π})$

Små svängningar ger att $\sin (θ) \approx θ$ så vi får slutligen följande rörelseekvation:

$\overset{. .}{θ} + \frac{8}{9 π - 16} \frac{g}{R} θ = 0$

Koefficienten till $θ$ är vår naturliga frekvens i kvadrat så vi har att:

$ω_{n} = \sqrt{\frac{8}{9 π - 16}} \sqrt{\frac{g}{R}} \approx 0.807 \sqrt{\frac{g}{R}}$

Vilket i sin tur ger perioden för vår svängning som:

$τ = \frac{2 π}{ω_{n}} = 7.78 \sqrt{\frac{R}{g}}$

Med det sagt, om du skulle välja punkten C som referens istället, skulle rörelseekvationen jag ställt upp ramla ut automatiskt om du deriverade total energi.

Tack för ditt svar!

Det är sant att uppgiften är tagen från Meriam-Kraige upplaga 7, vi har dock upplaga 8 som kursbok och i den ligger denna uppgift (inte exakt denna, men snarlik) under avsnittet "Energy methods". Dessutom var ett tips till uppgiften, som syns i den bifogade bilden, att använda energimetoden. Jag håller dock med dig om att det verkar rimligt att använda momentekvationer.

Kan man välja C som referenspunkt både i momentmetoden och energimetoden just för att C är momentant fix?

Jag undrar även varför $I_{C}$ ser ut som den gör i det här fallet, om vi använder parallellförflyttningssatsen borde vi väl få $I_{C} = I_{G} + m ({(R - \bar{r})}^{2} + r^{2} \sin^{2} (θ))$ , dvs $I_{C} = I_{G} + m [a v s t å n d t i l l G f r å n C]^{2}$ . $(R - \bar{r})$ är ju inte avståndet från C till G i varje ögonblick, eftersom C alltid är kontaktpunkten mellan cylinder och golv.

Spännande, den är nämligen under energy methods i utgåva 6.

Hursomhelst, som jag skrev i första posten är det bäst i detta fall att sätta maximal potentiell energi lika med maximal kinetisk energi eftersom det rör sig om harmonisk svängning. I min andra post skrev jag att du kan derivera total energi och då kommer du få fram den rörelseekvation jag ställde upp.

Det är inte så mycket att C är momentant fix som det är att det är punkten kroppen svänger kring approximativt för små svängningar. För större svängningar hade uppgiften blivit väldigt komplicerad. Du kan inte välja O eftersom det är en annan situation, den där semicylindern sitter ledad i O och svänger kring den.

Om du utvecklar ditt uttryck för masströghetsmomentet har vi:

$I_{C} = I_{G} + m (R^{2} - 2 R \bar{r} + {\bar{r}}^{2} + {\bar{r}}^{2} \sin^{2} (θ))$

Om vi bara tittar på term nummer två i högerled och vi vet att vid små svängningar är $\sin (θ) \approx θ$ :

$m (R^{2} - 2 R \bar{r} + {\bar{r}}^{2} + {\bar{r}}^{2} \sin^{2} (θ)) = m (R^{2} - 2 R \bar{r} + {\bar{r}}^{2} (1 + θ^{2}))$

Eftersom det är små svängningar är $θ^{2} < < 1$ så vi får att:

$m (R^{2} - 2 R \bar{r} + {\bar{r}}^{2} (1 + θ^{2})) = m (R^{2} - 2 R \bar{r} + {\bar{r}}^{2}) = m (R - \bar{r})^{2}$

Detta betyder i praktiken att det horisontella bidraget av hävarm till masströghetsmomentet är försumbart för små svängningar.

Tack så mycket för din hjälp! Det har verkligen blivit klarare nu. Jag inser att jag inte har använt mig av att det är små svängningar, vilket gjorde att jag inte riktigt kunde förstå rörelsen eller hur kroppen roterade. Jag är inte så van vid att använda sådana här approximationer, men man får väl vänja sig när man läser mekanik :)

pixisdot skrev:
Tack så mycket för din hjälp! Det har verkligen blivit klarare nu. Jag inser att jag inte har använt mig av att det är små svängningar, vilket gjorde att jag inte riktigt kunde förstå rörelsen eller hur kroppen roterade. Jag är inte så van vid att använda sådana här approximationer, men man får väl vänja sig när man läser mekanik :)

Det är främst för att du håller på med vibrationer/svängningar i just det kapitlet. Större, odämpade rörelser är ofta oförutsägbara och kaotiska i verkligheten vilket är varför de inte modelleras utom när de är strikt kontrollerade. Inom vibrationsmekanik använder man sig av taylorserier och fourierserier med olika trunkeringar av serien för att approximera rörelsen. Det är verkligen ingenjörskonst som ligger bakom och pionjärerna inom berättade inte för någon hur de räknade innan ålderns höst var kommen vilket gjorde att de kunde tjäna en bra peng.

Hanteringen av system med approximationer återkommer framförallt i hållfasthetslära, där har du något att se fram emot.

Svara Avbryt

Visa senaste svar