Uttryck för pendelkula
Hej,
jag försöker lösa denna uppgift: "En pendelkula hänger i en tråd med längden l meter och släpps från utslagsvinkeln 60 grader. När kulan passerar det lägsta läget, vid läget h, brister snöret. Skriv ett algebraiskt uttryck för hur långt bort i horisontell riktning från detta läge kulan träffar golvet."
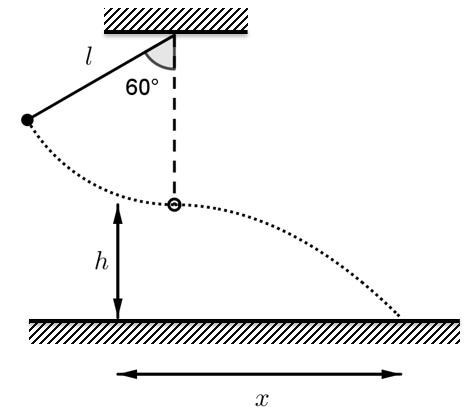
Jag har använt l*cos(60) för att räkna ut höjden över h som kulan är i från början.
Sedan energiprincipen mg(h+l/2)=mv^2/2 -> v=
Därefter tog jag h=gt^2/2 -> t=
x=t*vx -> * men får inte rätt på svaret som ska bli
Har prov imorgon och uppskattar snabbt svar. Tack
Hej och välkomment till Pluggakuten.
Nästan rätt!
När kulan passerar sin lägsta punkt har kulan "fallit" i y-led, från sin ursprungsposition till höjden h över marken (rött i bilden):
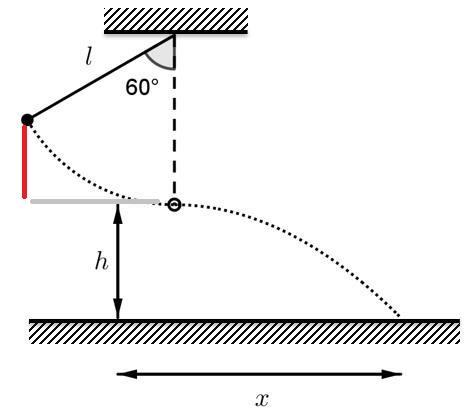
Nu har all förlust i lägesenergi omvandlats till hastighet i x-led. Kulan har "slutat falla", så vy=0 och energiprincipen ger:
Sedan har du räknat ut tiden att falla h alldeles korrekt.
Tack för snabbt svar. Jag fattar nu!
Lycka till! Sedan är ju bilden missvisande. Det markerade avståndet x är ju längre än ditt uträknade, eftersom det sträcker sig till vänster om kulans lägsta position. Det hade varit rimligt att rita h från kulans lägsta position och sedan x därifrån och till höger.

