Vad är sannolikheten att minst 8 av de 14 variablerna antar ett värde som är större än m?
Antag att ξ1,...,ξ14 är
oberoende och har samma kontinuerliga fördelning. Medianen m i fördelningen är lika med
0.65. Vad är sannolikheten att minst 8 av de 14 variablerna antar ett värde som är större än
m?
Så har suttit med frågan någon timme nu och kan inte förstå vad jag ska göra.
Ifall om någon skulle kunna knuffa mig till rätt spår skulle jag vara tacksam.
Median betyder att det är 50% sannolikhet på varje sida. Så du kan jämföra det med att singla slant 14 ggr.
Micimacko skrev:Median betyder att det är 50% sannolikhet på varje sida. Så du kan jämföra det med att singla slant 14 ggr.
Så svaret bör vara (1/2)^14?
Eller är det upphöjt med 8
Tror inte du vill räkna ut det för hand. Vilken fördelning får man från att singla slant?
Micimacko skrev:Tror inte du vill räkna ut det för hand. Vilken fördelning får man från att singla slant?
Så då har 50 50 chans. Så är svaret att varje kast är just det. En 50 chans att vara större än medianen?
Ja varje kast har 50 procent chans att vara större än medianen. Så låt Xi=1 om ξi är större än medianen och 0 annars. Vilken fördelning följer Xi? Vilken fördelning följer summan av de fjorton stycken Xi?
Hondel skrev:Ja varje kast har 50 procent chans att vara större än medianen. Så låt Xi=1 om ξi är större än medianen och 0 annars. Vilken fördelning följer Xi? Vilken fördelning följer summan av de fjorton stycken Xi?
Om jag förstår rätt så bör Xi = 0.5 och summan av alla 14 bör vara 1.
Tänker jag rätt nu?
Nej, Xi är antingen 1 eller 0. Det är som att du singlat slant och antingen visar slanten 1 vilket betyder "större än 0.65" eller 0 vilket betyder "mindre än 0.65". Frågan är sedan att minst 8 av de 14 variablerna ska vara större än 0.65, vilket betyder att summan av alla Xi är minst 8.
Lite mer ledning
Xi följer en Bernoulli-fördelning med parameter p=0.65. En summa av Bernoullivariabler (X1+X2+...+X14) följer en Binomialfördelning.
EDIT: tidigare stod det att Xi följer en binomialfördelning. Det ska vara en Bernoullifördelning
Hondel skrev:Nej, Xi är antingen 1 eller 0. Det är som att du singlat slant och antingen visar slanten 1 vilket betyder "större än 0.65" eller 0 vilket betyder "mindre än 0.65". Frågan är sedan att minst 8 av de 14 variablerna ska vara större än 0.65, vilket betyder att summan av alla Xi är minst 8.
Lite mer ledning
Xi följer en Binomial-fördelning med parameter p=0.65. En summa av binomialvariabler (X1+X2+...+X14) följer en Binomialfördelning.
Vad jag har skrivit nu är . Eller ska p = 0,65 istället för 0,5? Läste i boken och det står att p = är sannolikheten att det inträffar.
P ska vara 0,5. Men nu har du bara sannolikheten för att få exakt 8, inte fler än 8. Har du någon tabell med binomialfördelning i?
Micimacko skrev:P ska vara 0,5. Men nu har du bara sannolikheten för att få exakt 8, inte fler än 8. Har du någon tabell med binomialfördelning i?
Då jag gissar att jag ska titta där n = 14, x = 8 och där p = 0.5
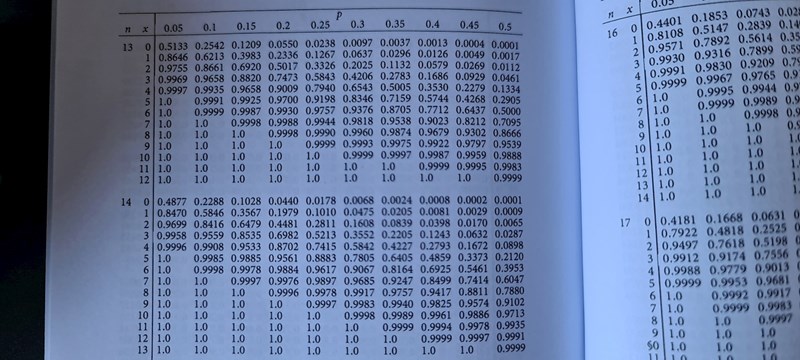
Nja, du tänker rätt, men tabellen visar sannolikheten att få mindre än eller lika med, så du ska titta på x<=7, alltså de fall du vill ta bort.
Micimacko skrev:Nja, du tänker rätt, men tabellen visar sannolikheten att få mindre än eller lika med, så du ska titta på x<=7, alltså de fall du vill ta bort.
Jaha då förstår jag men vad menar ni med "fall du vill ta bort". Vad jag förstår av det är att vi tar värdet ifrån x <= 7.
Sedan 1- (x<=7) då jag får lika med 0,3953, vilket borde vara vad x>=7 är. Så jag antar och hoppas det är svaret.
Komplementhändelsen.
Apoas skrev:Micimacko skrev:Nja, du tänker rätt, men tabellen visar sannolikheten att få mindre än eller lika med, så du ska titta på x<=7, alltså de fall du vill ta bort.
Jaha då förstår jag men vad menar ni med "fall du vill ta bort". Vad jag förstår av det är att vi tar värdet ifrån x <= 7.
Sedan 1- (x<=7) då jag får lika med 0,3953, vilket borde vara vad x>=7 är. Så jag antar och hoppas det är svaret.
Det låter rätt, en liten kommentar bara är att 1-p(x<=7) är p(x>7), alltså sannolikheten att x är strikt större än 7. Och eftersom x bara är heltal är det samma sak som att säga x>=8, vilket var vad frågades efter



