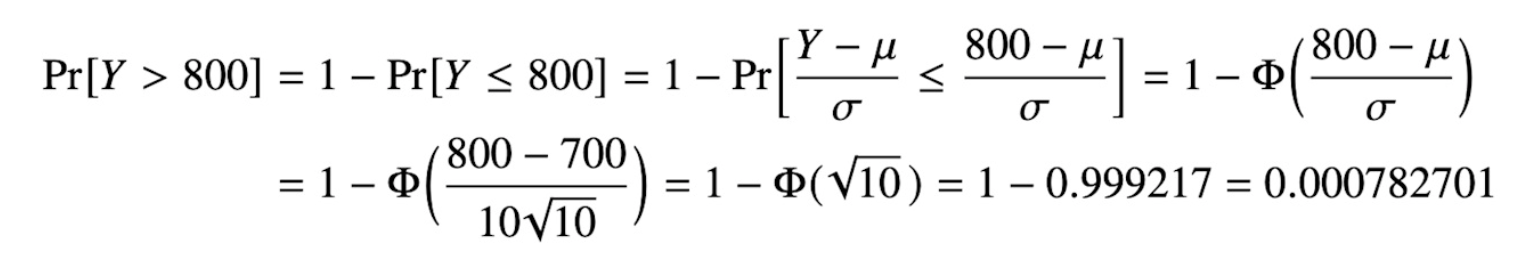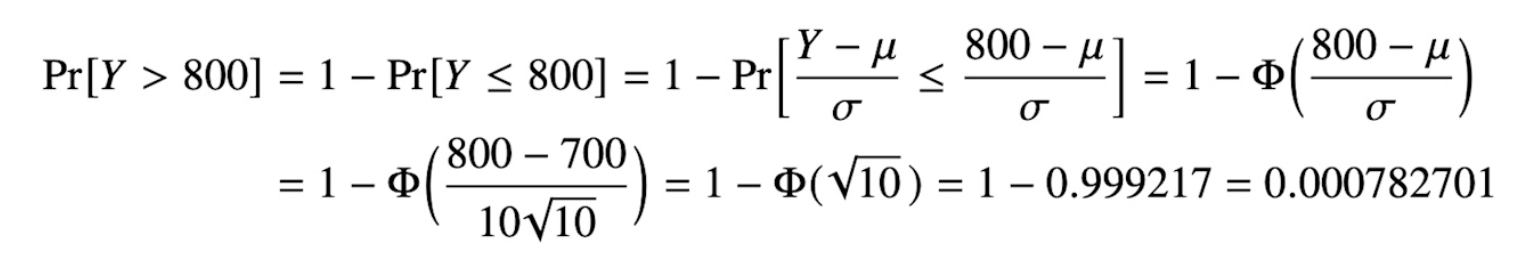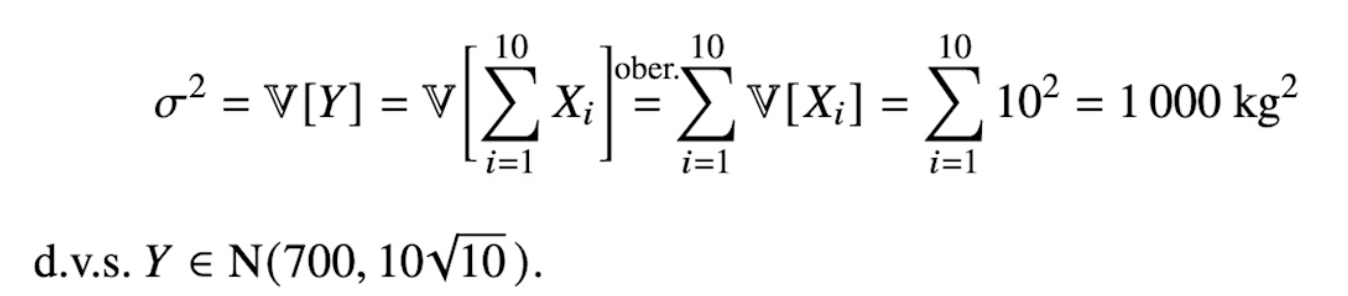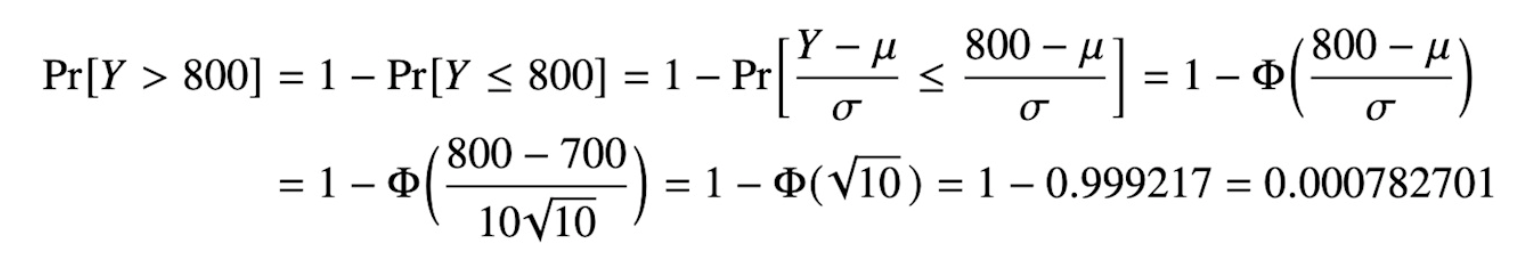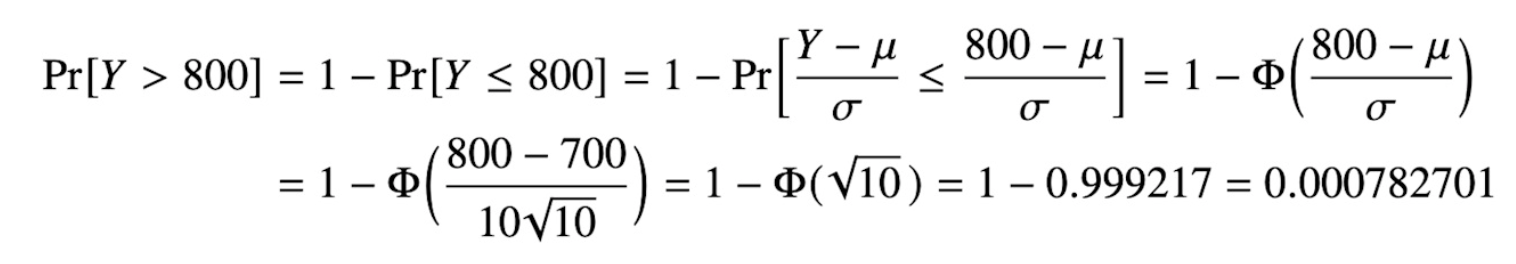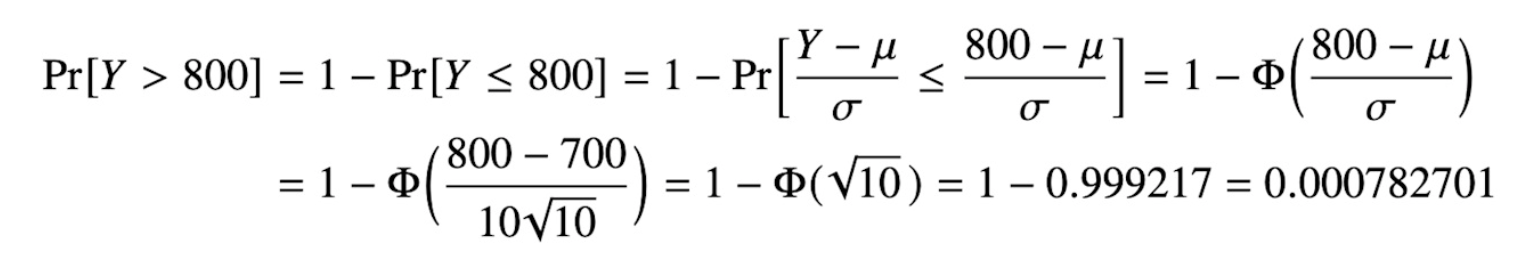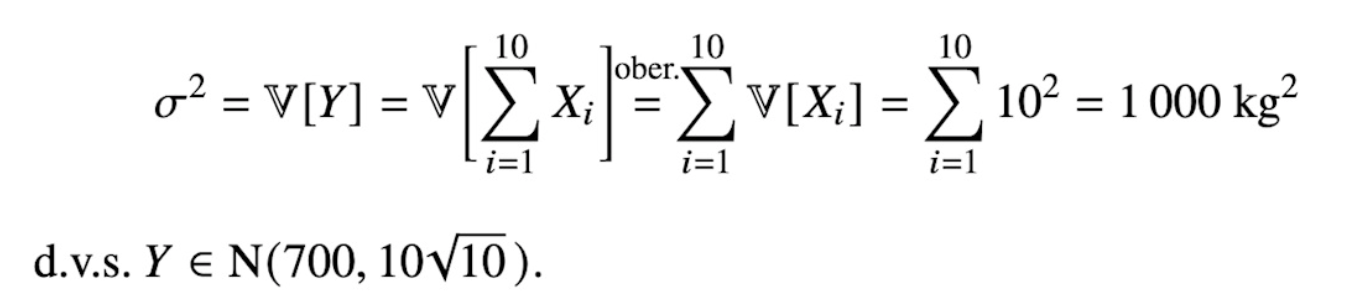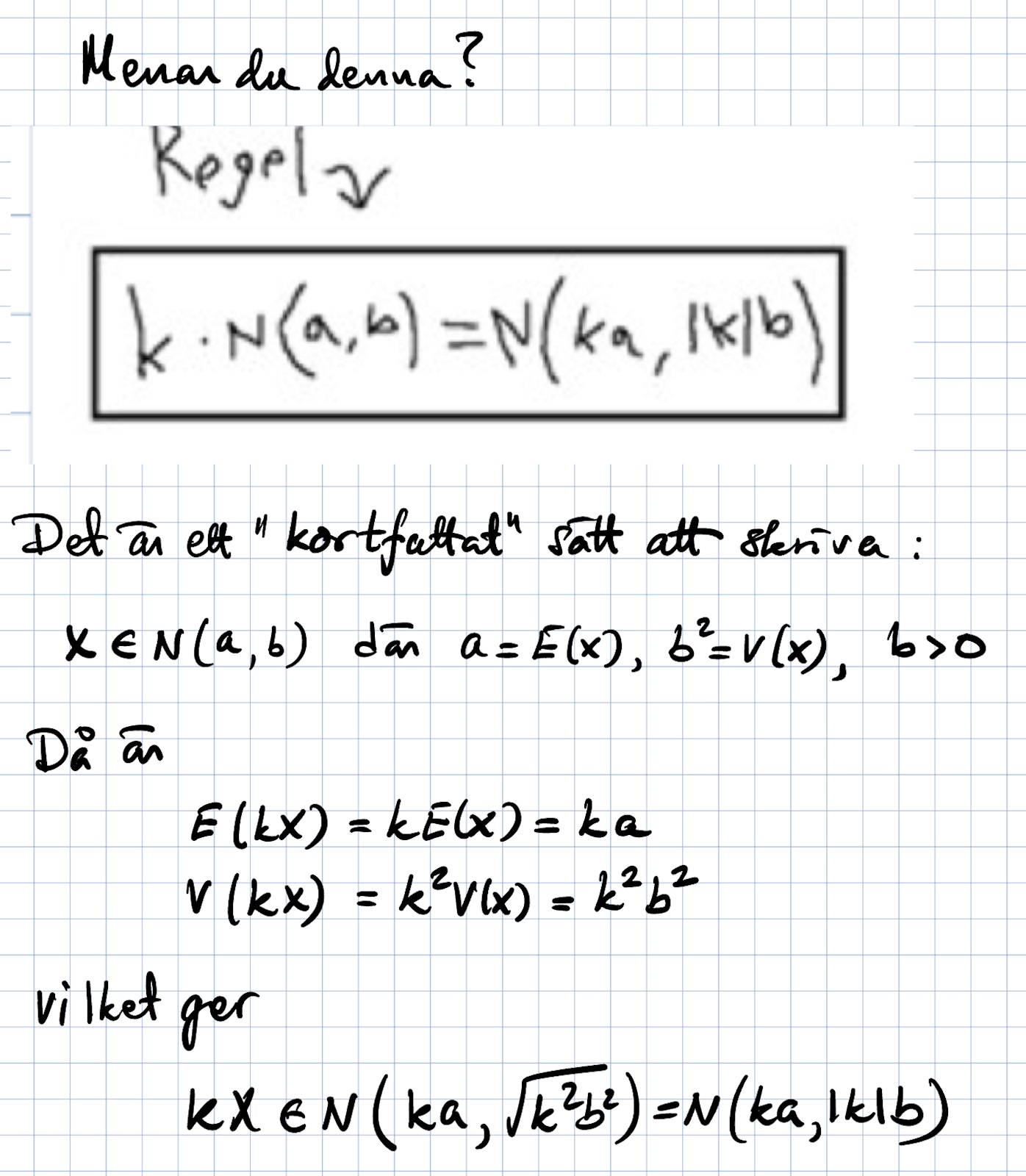Vad är sannolikheten för att 10 vuxna personer överlastar hissen?
Hej!
Jag körde fast på denna uppgift. Hur går man till väga? Söker de P(X>=10) eller P(X>=800)?

destiny99 skrev:Hej!
Jag körde fast på denna uppgift. Hur går man till väga? Söker de P(X>=10) eller P(X>=800)?
Ett utdrag från min kommande kioskvältare;

Viss variation in Phi-värde kan ske beroende på hur man beräknar detta, men verktyg eller med tabell.
Trinity2 skrev:destiny99 skrev:Hej!
Jag körde fast på denna uppgift. Hur går man till väga? Söker de P(X>=10) eller P(X>=800)?
Ett utdrag från min kommande kioskvältare;
Viss variation in Phi-värde kan ske beroende på hur man beräknar detta, men verktyg eller med tabell.
Oj det var exakt detta jag ville använda. Men vad bra! Testar själv och ser om jag får samma sak. Fast jag tänkte använda P (800-700/10)=phi(100) men jag ser att du tar 10sqrt(10) inämnaren så jag hänger ej alls med på vad du gör där och sen tar du 1-phi(...)
destiny99 skrev:Trinity2 skrev:destiny99 skrev:Hej!
Jag körde fast på denna uppgift. Hur går man till väga? Söker de P(X>=10) eller P(X>=800)?
Ett utdrag från min kommande kioskvältare;
Viss variation in Phi-värde kan ske beroende på hur man beräknar detta, men verktyg eller med tabell.
Oj det var exakt detta jag ville använda. Men vad bra! Testar själv och ser om jag får samma sak. Fast jag tänkte använda P (800-700/10)=phi(100) men jag ser att du tar 10sqrt(10) inämnaren så jag hänger ej alls med på vad du gör där och sen tar du 1-phi(...)
800-700=100
100/(10sqrt(10)) = 10/sqrt(10) = sqrt(10)
Är du med?
1-PHI kommer av att vi söker Y>800 men "vänder på det" till Y≤800
Trinity2 skrev:destiny99 skrev:Trinity2 skrev:destiny99 skrev:Hej!
Jag körde fast på denna uppgift. Hur går man till väga? Söker de P(X>=10) eller P(X>=800)?
Ett utdrag från min kommande kioskvältare;
Viss variation in Phi-värde kan ske beroende på hur man beräknar detta, men verktyg eller med tabell.
Oj det var exakt detta jag ville använda. Men vad bra! Testar själv och ser om jag får samma sak. Fast jag tänkte använda P (800-700/10)=phi(100) men jag ser att du tar 10sqrt(10) inämnaren så jag hänger ej alls med på vad du gör där och sen tar du 1-phi(...)
800-700=100
100/(10sqrt(10)) = 10/sqrt(10) = sqrt(10)
Är du med?
1-PHI kommer av att vi söker Y>800 men "vänder på det" till Y≤800
Nope jag är inte med på vad du gör..
destiny99 skrev:Trinity2 skrev:destiny99 skrev:Trinity2 skrev:destiny99 skrev:Hej!
Jag körde fast på denna uppgift. Hur går man till väga? Söker de P(X>=10) eller P(X>=800)?
Ett utdrag från min kommande kioskvältare;
Viss variation in Phi-värde kan ske beroende på hur man beräknar detta, men verktyg eller med tabell.
Oj det var exakt detta jag ville använda. Men vad bra! Testar själv och ser om jag får samma sak. Fast jag tänkte använda P (800-700/10)=phi(100) men jag ser att du tar 10sqrt(10) inämnaren så jag hänger ej alls med på vad du gör där och sen tar du 1-phi(...)
800-700=100
100/(10sqrt(10)) = 10/sqrt(10) = sqrt(10)
Är du med?
1-PHI kommer av att vi söker Y>800 men "vänder på det" till Y≤800
Nope jag är inte med på vad du gör..

Det första steget är bara en "vändning".
Sedan sker en "normering" av Y till en N(0,1)-s.v. varpå vi kan använda Phi-funktionen
Trinity2 skrev:destiny99 skrev:Trinity2 skrev:destiny99 skrev:Trinity2 skrev:destiny99 skrev:Hej!
Jag körde fast på denna uppgift. Hur går man till väga? Söker de P(X>=10) eller P(X>=800)?
Ett utdrag från min kommande kioskvältare;
Viss variation in Phi-värde kan ske beroende på hur man beräknar detta, men verktyg eller med tabell.
Oj det var exakt detta jag ville använda. Men vad bra! Testar själv och ser om jag får samma sak. Fast jag tänkte använda P (800-700/10)=phi(100) men jag ser att du tar 10sqrt(10) inämnaren så jag hänger ej alls med på vad du gör där och sen tar du 1-phi(...)
800-700=100
100/(10sqrt(10)) = 10/sqrt(10) = sqrt(10)
Är du med?
1-PHI kommer av att vi söker Y>800 men "vänder på det" till Y≤800
Nope jag är inte med på vad du gör..
Det första steget är bara en "vändning".
Sedan sker en "normering" av Y till en N(0,1)-s.v. varpå vi kan använda Phi-funktionen
Aa asså jag är tyvärr inte med. Såhär vill jag göra. Se bild

destiny99 skrev:Trinity2 skrev:destiny99 skrev:Trinity2 skrev:destiny99 skrev:Trinity2 skrev:destiny99 skrev:Hej!
Jag körde fast på denna uppgift. Hur går man till väga? Söker de P(X>=10) eller P(X>=800)?
Ett utdrag från min kommande kioskvältare;
Viss variation in Phi-värde kan ske beroende på hur man beräknar detta, men verktyg eller med tabell.
Oj det var exakt detta jag ville använda. Men vad bra! Testar själv och ser om jag får samma sak. Fast jag tänkte använda P (800-700/10)=phi(100) men jag ser att du tar 10sqrt(10) inämnaren så jag hänger ej alls med på vad du gör där och sen tar du 1-phi(...)
800-700=100
100/(10sqrt(10)) = 10/sqrt(10) = sqrt(10)
Är du med?
1-PHI kommer av att vi söker Y>800 men "vänder på det" till Y≤800
Nope jag är inte med på vad du gör..
Det första steget är bara en "vändning".
Sedan sker en "normering" av Y till en N(0,1)-s.v. varpå vi kan använda Phi-funktionen
Aa asså jag är tyvärr inte med. Såhär vill jag göra. Se bild
Men std-av. är ej 10.

Rent allmänt, OFTA (men inte alltid) i dessa uppgifter är argumentet till Phi "rimligt", dvs inte så stort till absolutbeloppet. Så får du -24 eller +12 som argument har du säkerligen räknat fel.
Trinity2 skrev:destiny99 skrev:Trinity2 skrev:destiny99 skrev:Trinity2 skrev:destiny99 skrev:Trinity2 skrev:destiny99 skrev:Hej!
Jag körde fast på denna uppgift. Hur går man till väga? Söker de P(X>=10) eller P(X>=800)?
Ett utdrag från min kommande kioskvältare;
Viss variation in Phi-värde kan ske beroende på hur man beräknar detta, men verktyg eller med tabell.
Oj det var exakt detta jag ville använda. Men vad bra! Testar själv och ser om jag får samma sak. Fast jag tänkte använda P (800-700/10)=phi(100) men jag ser att du tar 10sqrt(10) inämnaren så jag hänger ej alls med på vad du gör där och sen tar du 1-phi(...)
800-700=100
100/(10sqrt(10)) = 10/sqrt(10) = sqrt(10)
Är du med?
1-PHI kommer av att vi söker Y>800 men "vänder på det" till Y≤800
Nope jag är inte med på vad du gör..
Det första steget är bara en "vändning".
Sedan sker en "normering" av Y till en N(0,1)-s.v. varpå vi kan använda Phi-funktionen
Aa asså jag är tyvärr inte med. Såhär vill jag göra. Se bild
Men std-av. är ej 10.
Jag förstår inte uppgiften isåfall. Det hjälper inte med lösningsförslag för jag undrar vad N(70,10) är.
destiny99 skrev:Trinity2 skrev:destiny99 skrev:Trinity2 skrev:destiny99 skrev:Trinity2 skrev:destiny99 skrev:Trinity2 skrev:destiny99 skrev:Hej!
Jag körde fast på denna uppgift. Hur går man till väga? Söker de P(X>=10) eller P(X>=800)?
Ett utdrag från min kommande kioskvältare;
Viss variation in Phi-värde kan ske beroende på hur man beräknar detta, men verktyg eller med tabell.
Oj det var exakt detta jag ville använda. Men vad bra! Testar själv och ser om jag får samma sak. Fast jag tänkte använda P (800-700/10)=phi(100) men jag ser att du tar 10sqrt(10) inämnaren så jag hänger ej alls med på vad du gör där och sen tar du 1-phi(...)
800-700=100
100/(10sqrt(10)) = 10/sqrt(10) = sqrt(10)
Är du med?
1-PHI kommer av att vi söker Y>800 men "vänder på det" till Y≤800
Nope jag är inte med på vad du gör..
Det första steget är bara en "vändning".
Sedan sker en "normering" av Y till en N(0,1)-s.v. varpå vi kan använda Phi-funktionen
Aa asså jag är tyvärr inte med. Såhär vill jag göra. Se bild
Men std-av. är ej 10.
Jag förstår inte uppgiften isåfall. Det hjälper inte med lösningsförslag för jag undrar vad N(70,10) är.
N(mu,sigma) är koden för "Normalfördelning med väntevärde mu och std-av. sigma". Står det inte i din bok? Det har funnits med i säkert 30+ år i kurserna.
Trinity2 skrev:destiny99 skrev:Trinity2 skrev:destiny99 skrev:Trinity2 skrev:destiny99 skrev:Trinity2 skrev:destiny99 skrev:Trinity2 skrev:destiny99 skrev:Hej!
Jag körde fast på denna uppgift. Hur går man till väga? Söker de P(X>=10) eller P(X>=800)?
Ett utdrag från min kommande kioskvältare;
Viss variation in Phi-värde kan ske beroende på hur man beräknar detta, men verktyg eller med tabell.
Oj det var exakt detta jag ville använda. Men vad bra! Testar själv och ser om jag får samma sak. Fast jag tänkte använda P (800-700/10)=phi(100) men jag ser att du tar 10sqrt(10) inämnaren så jag hänger ej alls med på vad du gör där och sen tar du 1-phi(...)
800-700=100
100/(10sqrt(10)) = 10/sqrt(10) = sqrt(10)
Är du med?
1-PHI kommer av att vi söker Y>800 men "vänder på det" till Y≤800
Nope jag är inte med på vad du gör..
Det första steget är bara en "vändning".
Sedan sker en "normering" av Y till en N(0,1)-s.v. varpå vi kan använda Phi-funktionen
Aa asså jag är tyvärr inte med. Såhär vill jag göra. Se bild
Men std-av. är ej 10.
Jag förstår inte uppgiften isåfall. Det hjälper inte med lösningsförslag för jag undrar vad N(70,10) är.
N(mu,sigma) är koden för "Normalfördelning med väntevärde mu och std-av. sigma". Står det inte i din bok? Det har funnits med i säkert 30+ år i kurserna.
Okej så vi har väntevärde 70 och sigma 10 eller hur? Vi har 10 personer och 800 kg. Vi vet inte vad väntevärde är för 10 personer och standardavvikelse eller sigma
destiny99 skrev:Trinity2 skrev:destiny99 skrev:Trinity2 skrev:destiny99 skrev:Trinity2 skrev:destiny99 skrev:Trinity2 skrev:destiny99 skrev:Trinity2 skrev:destiny99 skrev:Hej!
Jag körde fast på denna uppgift. Hur går man till väga? Söker de P(X>=10) eller P(X>=800)?
Ett utdrag från min kommande kioskvältare;
Viss variation in Phi-värde kan ske beroende på hur man beräknar detta, men verktyg eller med tabell.
Oj det var exakt detta jag ville använda. Men vad bra! Testar själv och ser om jag får samma sak. Fast jag tänkte använda P (800-700/10)=phi(100) men jag ser att du tar 10sqrt(10) inämnaren så jag hänger ej alls med på vad du gör där och sen tar du 1-phi(...)
800-700=100
100/(10sqrt(10)) = 10/sqrt(10) = sqrt(10)
Är du med?
1-PHI kommer av att vi söker Y>800 men "vänder på det" till Y≤800
Nope jag är inte med på vad du gör..
Det första steget är bara en "vändning".
Sedan sker en "normering" av Y till en N(0,1)-s.v. varpå vi kan använda Phi-funktionen
Aa asså jag är tyvärr inte med. Såhär vill jag göra. Se bild
Men std-av. är ej 10.
Jag förstår inte uppgiften isåfall. Det hjälper inte med lösningsförslag för jag undrar vad N(70,10) är.
N(mu,sigma) är koden för "Normalfördelning med väntevärde mu och std-av. sigma". Står det inte i din bok? Det har funnits med i säkert 30+ år i kurserna.
Okej så vi har väntevärde 70 och sigma 10 eller hur? Vi har 10 personer och 800 kg.
Ja, N(70,10) PER PERSON. Men det är SUMMAN av 10 personer och det är inte N(70,10).
Trinity2 skrev:destiny99 skrev:Trinity2 skrev:destiny99 skrev:Trinity2 skrev:destiny99 skrev:Trinity2 skrev:destiny99 skrev:Trinity2 skrev:destiny99 skrev:Trinity2 skrev:destiny99 skrev:Hej!
Jag körde fast på denna uppgift. Hur går man till väga? Söker de P(X>=10) eller P(X>=800)?
Ett utdrag från min kommande kioskvältare;
Viss variation in Phi-värde kan ske beroende på hur man beräknar detta, men verktyg eller med tabell.
Oj det var exakt detta jag ville använda. Men vad bra! Testar själv och ser om jag får samma sak. Fast jag tänkte använda P (800-700/10)=phi(100) men jag ser att du tar 10sqrt(10) inämnaren så jag hänger ej alls med på vad du gör där och sen tar du 1-phi(...)
800-700=100
100/(10sqrt(10)) = 10/sqrt(10) = sqrt(10)
Är du med?
1-PHI kommer av att vi söker Y>800 men "vänder på det" till Y≤800
Nope jag är inte med på vad du gör..
Det första steget är bara en "vändning".
Sedan sker en "normering" av Y till en N(0,1)-s.v. varpå vi kan använda Phi-funktionen
Aa asså jag är tyvärr inte med. Såhär vill jag göra. Se bild
Men std-av. är ej 10.
Jag förstår inte uppgiften isåfall. Det hjälper inte med lösningsförslag för jag undrar vad N(70,10) är.
N(mu,sigma) är koden för "Normalfördelning med väntevärde mu och std-av. sigma". Står det inte i din bok? Det har funnits med i säkert 30+ år i kurserna.
Okej så vi har väntevärde 70 och sigma 10 eller hur? Vi har 10 personer och 800 kg.
Ja, N(70,10) PER PERSON. Men det är SUMMAN av 10 personer och det är inte N(70,10).
Nu hänger jag inte med. Var inte N(70,10) normalfördelning för väntevärde 70 och sigma 10? Jag vet inte hur uppgiften skall tolkas men allt jag ser är att vi saknar väntevärde och sigma för den här 800 kg.
Men hur tar man reda på sigma och väntevärde?
Det är något sådant vi ska göra. Men hur hittar man den där regel där man multiplicerae in koefficienten i N(my,o/sqrt(n)) dvs kN(a,b)=N(ka,|k|b)?
Här är en bild från boken


Vad menar du med |k| här?
Laguna skrev:Vad menar du med |k| här?
Vet ej en kursare skrev så.
Stämmer, variansen kan aldrig vara negativ, så en linjärkombination med negativa koefficienter måste ha en positiv varians
Trinity2 skrev:
Så var kommer det här multiplikationen med 10 i N(u,o/sqrt(n)) ifrån så att vi får 10*70,sqrt(10)*10? Det har inte förklarats ännu.
Trinity2 skrev:Stämmer, variansen kan aldrig vara negativ, så en linjärkombination med negativa koefficienter måste ha en positiv varians
Vilken regel säger detta?
destiny99 skrev:Trinity2 skrev:Stämmer, variansen kan aldrig vara negativ, så en linjärkombination med negativa koefficienter måste ha en positiv varians
Vilken regel säger detta?
Logiken.
om X är N(0,1) och Y är N(3,1) har då X-Y varians 0? eller X-2Y varians <0? Hur skulle en sådan täthetsfunktion se ut?
Trinity2 skrev:destiny99 skrev:Trinity2 skrev:Stämmer, variansen kan aldrig vara negativ, så en linjärkombination med negativa koefficienter måste ha en positiv varians
Vilken regel säger detta?
Logiken.
om X är N(0,1) och Y är N(3,1) har då X-Y varians 0? eller X-2Y varians -1? Hur skulle en sådan täthetsfunktion se ut?
Nej jag har tyvärr ingen aning. Hur kan dessa ha varians 0 respektive -1? Varför multiplicerar man 10 inne i uttrycket för N(u,o/sqrt(n))?
destiny99 skrev:Trinity2 skrev:destiny99 skrev:Trinity2 skrev:Stämmer, variansen kan aldrig vara negativ, så en linjärkombination med negativa koefficienter måste ha en positiv varians
Vilken regel säger detta?
Logiken.
om X är N(0,1) och Y är N(3,1) har då X-Y varians 0? eller X-2Y varians -1? Hur skulle en sådan täthetsfunktion se ut?
Nej jag har tyvärr ingen aning.
Det måste finnas en utläggnng om detta i läroboken. I BLom är det sats 5.11
Variansen är väntevärdet av kvadrerade avvikelser från väntevärdet och kvadrerade tal summeras alltid till >0 för fördelningar som har varians.
En "stokastisk variabel" som är konstant har ingen varians, men då är det inte heller så stokastisk.
Trinity2 skrev:destiny99 skrev:Trinity2 skrev:destiny99 skrev:Trinity2 skrev:Stämmer, variansen kan aldrig vara negativ, så en linjärkombination med negativa koefficienter måste ha en positiv varians
Vilken regel säger detta?
Logiken.
om X är N(0,1) och Y är N(3,1) har då X-Y varians 0? eller X-2Y varians -1? Hur skulle en sådan täthetsfunktion se ut?
Nej jag har tyvärr ingen aning.
Det måste finnas en utläggnng om detta i läroboken. I BLom är det sats 5.11
Variansen är väntevärdet av kvadrerade avvikelser från väntevärdet och kvadrerade tal summeras alltid till >0 för fördelningar som har varians.
En "stokastisk variabel" som är konstant har ingen varians, men då är det inte heller så stokastisk.
Ok jag tittar på sats 5.11 imorgon.
" Variansen är väntevärdet av kvadrerade avvikelser från väntevärdet och kvadrerade tal summeras alltid till >0 för fördelningar som har varians"
Denna är från boken eller?
Kan du bara typ förklara varför man multiplicerar den där k-faktorn inne i N(u,o/sqrt(n))? Jag vet att det är en regel, men denna regel hittar jag inte exakt i boken sist jag kollade. Annars förstår jag hela beräkningen fram till slutsvaret
destiny99 skrev:Trinity2 skrev:destiny99 skrev:Trinity2 skrev:destiny99 skrev:Trinity2 skrev:Stämmer, variansen kan aldrig vara negativ, så en linjärkombination med negativa koefficienter måste ha en positiv varians
Vilken regel säger detta?
Logiken.
om X är N(0,1) och Y är N(3,1) har då X-Y varians 0? eller X-2Y varians -1? Hur skulle en sådan täthetsfunktion se ut?
Nej jag har tyvärr ingen aning.
Det måste finnas en utläggnng om detta i läroboken. I BLom är det sats 5.11
Variansen är väntevärdet av kvadrerade avvikelser från väntevärdet och kvadrerade tal summeras alltid till >0 för fördelningar som har varians.
En "stokastisk variabel" som är konstant har ingen varians, men då är det inte heller så stokastisk.
Ok jag tittar på sats 5.11 imorgon.
" Variansen är väntevärdet av kvadrerade avvikelser från väntevärdet och kvadrerade tal summeras alltid till >0 för fördelningar som har varians"
Denna är från boken eller?
Kan du bara typ förklara varför man multiplicerar den där k-faktorn inne i N(u,o/sqrt(n))? Jag vet att det är en regel, men denna regel hittar jag inte exakt i boken sist jag kollade. Annars förstår jag hela beräkningen fram till slutsvaret
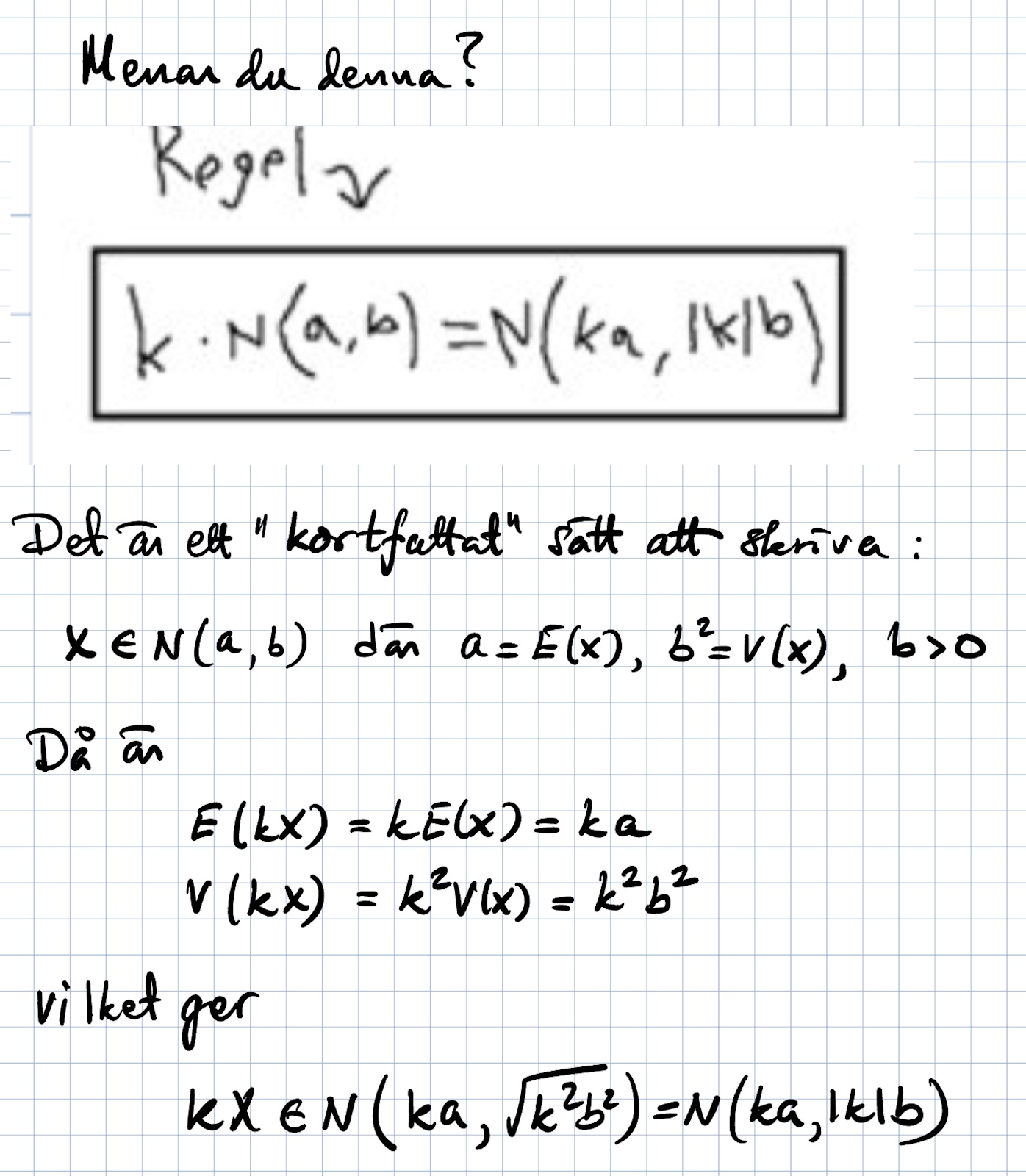
Trinity2 skrev:destiny99 skrev:Trinity2 skrev:destiny99 skrev:Trinity2 skrev:destiny99 skrev:Trinity2 skrev:Stämmer, variansen kan aldrig vara negativ, så en linjärkombination med negativa koefficienter måste ha en positiv varians
Vilken regel säger detta?
Logiken.
om X är N(0,1) och Y är N(3,1) har då X-Y varians 0? eller X-2Y varians -1? Hur skulle en sådan täthetsfunktion se ut?
Nej jag har tyvärr ingen aning.
Det måste finnas en utläggnng om detta i läroboken. I BLom är det sats 5.11
Variansen är väntevärdet av kvadrerade avvikelser från väntevärdet och kvadrerade tal summeras alltid till >0 för fördelningar som har varians.
En "stokastisk variabel" som är konstant har ingen varians, men då är det inte heller så stokastisk.
Ok jag tittar på sats 5.11 imorgon.
" Variansen är väntevärdet av kvadrerade avvikelser från väntevärdet och kvadrerade tal summeras alltid till >0 för fördelningar som har varians"
Denna är från boken eller?
Kan du bara typ förklara varför man multiplicerar den där k-faktorn inne i N(u,o/sqrt(n))? Jag vet att det är en regel, men denna regel hittar jag inte exakt i boken sist jag kollade. Annars förstår jag hela beräkningen fram till slutsvaret
Aa precis. Ska komma ihåg och anteckna ned detta för jag hittar inte exakt denna bevis som du skrev upp i boken.