Vad är skillnaden mellan dessa kopplingsscheman?
Har efter mycket vånda och stort besvär äntligen accepterat bilden av det första kopplingsschemat. Trodde då i min enfald att jag hade klart för mig hur det andra skulle vara och räknade glatt på ersättningsresistansen… som blev fel, för nu skulle det översättas enligt bilden till höger. De jag trodde låg parallellt (i enlighet med översta bilden), låg ju absolut inte parallellt med varandra…
känns ju jobbigt att man får fel innan man ens börjat räkna för att man inte förstår bilden.
HUR ska jag ”se rätt”!
Hejsan!
Det första man behöver veta är att kopplingarna (sladdarna) i schemat kan vara hur korta eller långa som helst. De kan även vara raka, böjda eller i räta vinklar utan att det spelar någon som helst roll för hur komponenterna är ihopkopplade. Det är ett kopplingsschema vars enda uppgift är att visa vad som är ihopkopplat med vad.
Kopplingarna kan man dela in i "noder" (kopplingspunkter). Du har redan två stycken markerade: P och Q. Om två komponenter är anslutna till samma noder, så är de parallellkopplade. Detta helt oavsett hur schemat är ritat.
Så här brukar jag göra:
Ta en färgpenna, en riktig eller en "mental". Börja vid batteriets pluspol. Jag väljer en röd och sedan färglägger jag alla anslutningar till pluspolen röda. Den noden heter P i ditt schema. Allt rött är nu P.
Sedan tar jag en blå penna och gör samma sak med minuspolen. Alla anslutningar dit blir blå. Vi har ingen bokstav för den noden, så jag kallar den R.
Nu har jag nästan färglagt alla kopplingar, men det finns lite kvar som varken är ansluten till plus eller minus. Den får bli lila, den som heter Q i ditt schema.
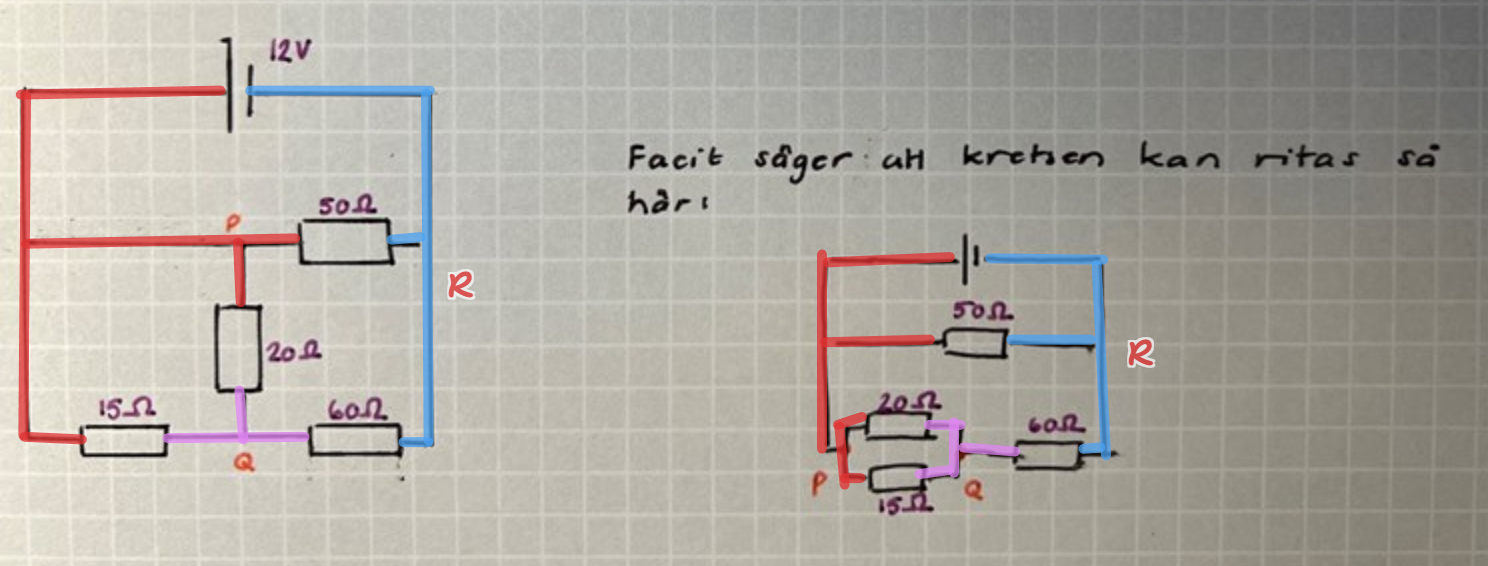
Nu tycker jag det är mycket lättare att se att 15 och 20 ohm är parallellkopplade. Ena sidan av motstånden är anslutna till den röda noden P; den andra sidan är ansluten till den lila Q. Eftersom de är anslutna till samma noder så är de parallellkopplade. Detta oberoende av om de är ritade snyggt bredvid varandra eller i vinkel.
Nu kan man också se att 60 ohm är seriekopplad med de parallellkopplade 15 och 20. Ena sidan av 60 är ansluten till Q och den andra till R.
Man kan också se att 50 ohm är parallellkopplad med de andra tre. Det är anslutet till den röda P och den blå Q.
Kort sagt: Du får dra, vrida, vända och förgrena kopplingarna hur. Tänk dig att de är gummiband som kan bli hur långa eller korta som helst. Det enda du inte får göra är att förändra hur komponenterna är inkopplade till respektive nod.
Blev det lite klarare? Fråga annars.
Ett fantastiskt svar! Så ambitiöst svarat - tack!
Jag fattade exakt!
Jag gillar färgtänket och ska anamma det och kika på andra uppgifter för att öva.
Dock… den övre kopplingen- den kan ju inte förenklas i mitten med färger? Den där lilla kopplingen i mitten (märkt Ib-ström) är lite speciell? För om jag ritar schemat som en seriekoppling mellan vänster och höger parallellkopplade ”klumpar”, då får man inte rätt på Ib-strömmen (som tas fram med Kirchhoffs första lag). Ber jag om för mycket om jag ber om hjälp att rita om det schemat också!
Kopplingen i mitten är rent elektriskt en och samma punkt. Den har en viss potential, en viss spänning. Det kommer absolut att flyta en ström igenom den. All ström i kretsen, från batteriets plus- till minuspolen kommer att passera där.
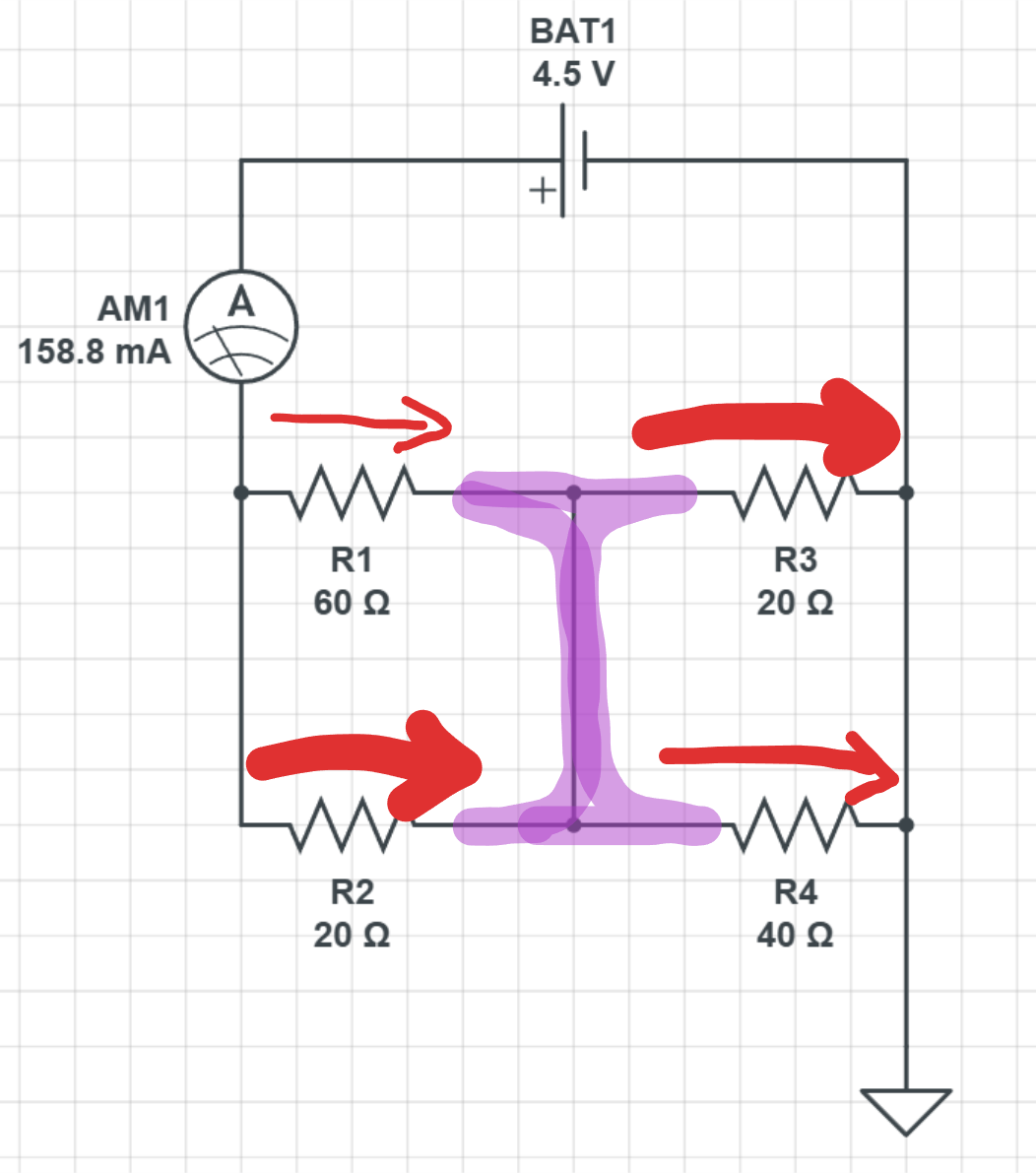
In till noden kommer det mycket ström genom R2 och mindre genom R1. Ut från den flyter mycket genom R3 och mindre genom R4. Hur mycket beror på resistansen.
Jag har kopplat in en amperemeter efter batteriet och den visar ca 159 mA. Det är bara för att ha lite koll.
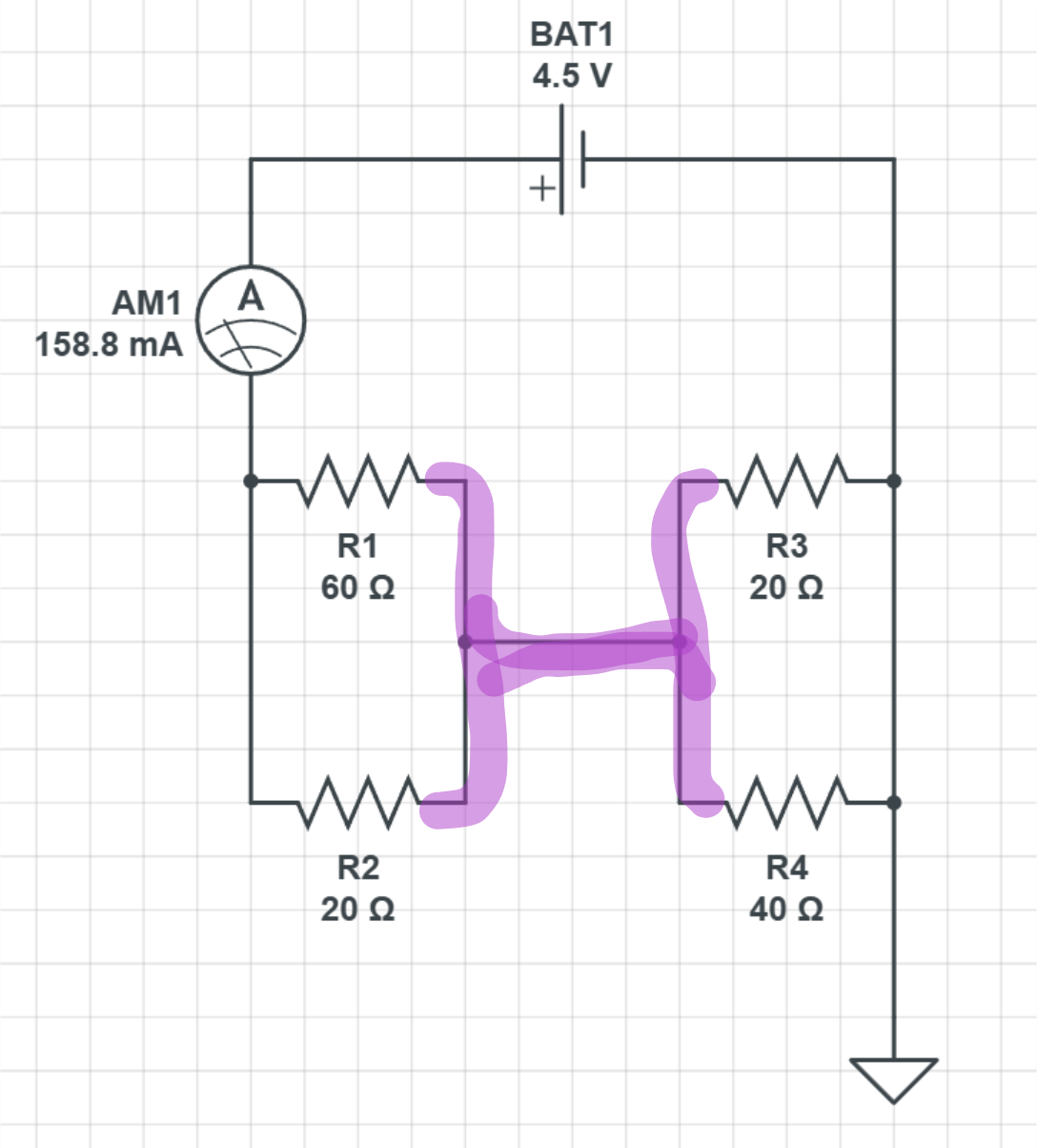
Om jag ritar om den lite så påverkar det förstås inte den totala strömmen genom kretsen alls. Den är fortfarande ca 159 mA.
Jag kan koppla in en amperemeter istället för en bit "sladd" bara för att visa att all ström går den vägen. Det är förstås också ca 159 mA och det finns ju ingen annan väg för strömmen att gå.
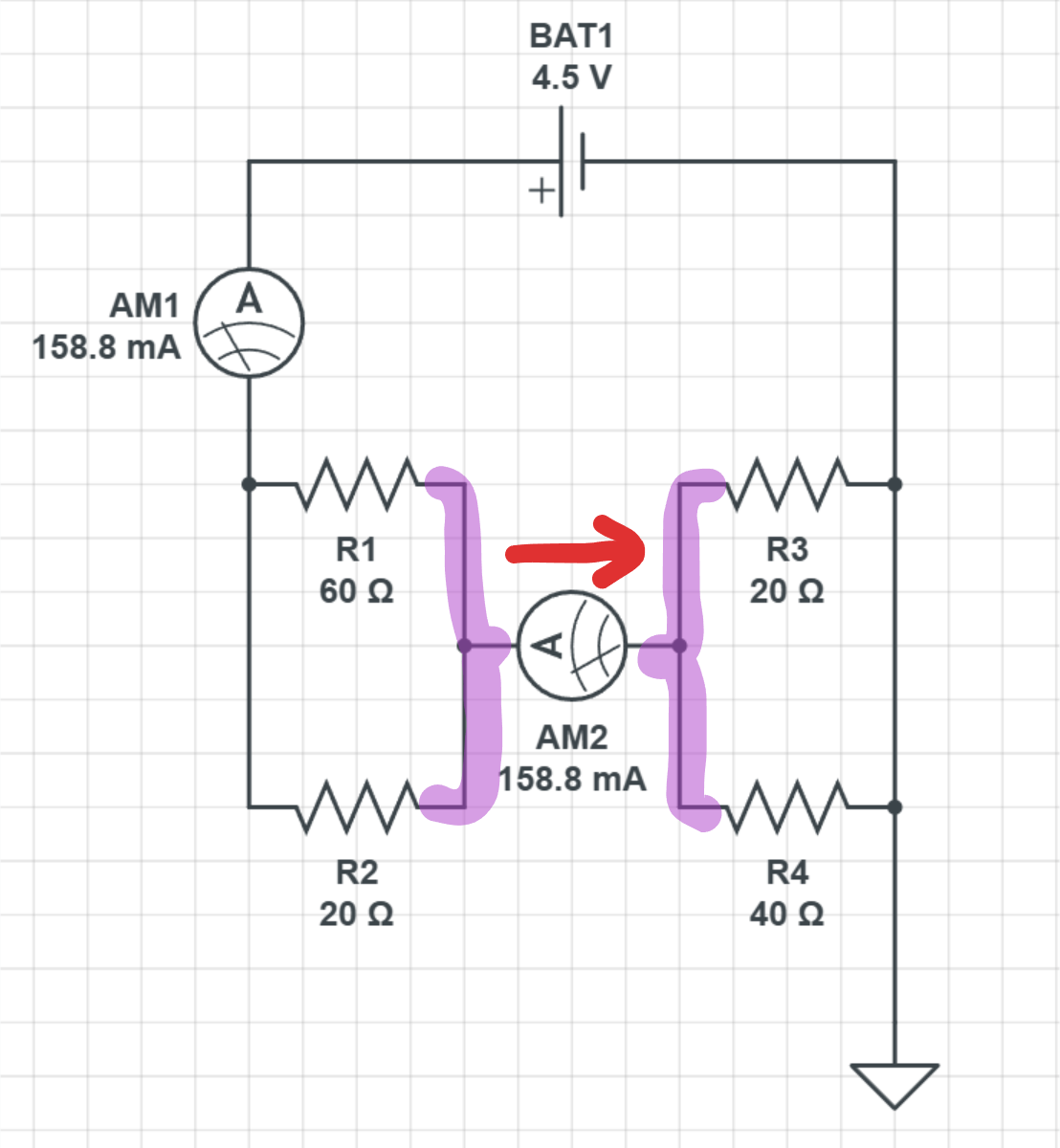
Nu kommer det trixiga, det som du egentligen frågade om.
Du vet ju att KSL (Kirchhoffs strömlag) säger att summan av ström in till en nod är lika med summan av strömmen ut ur en nod.
Den ström som flyter in via R1 och R2 skall lämna via R3 och R4.
Detta är nog inga problem att tänka sig om all ström går in och ut ur en gemensam oändligt liten punkt. Sådana finns ju inte i verkligheten. (Faktum är att resistansen i sladdarna inte heller är noll ohm som vi ofta räknar med, men vi struntar i det nu.)
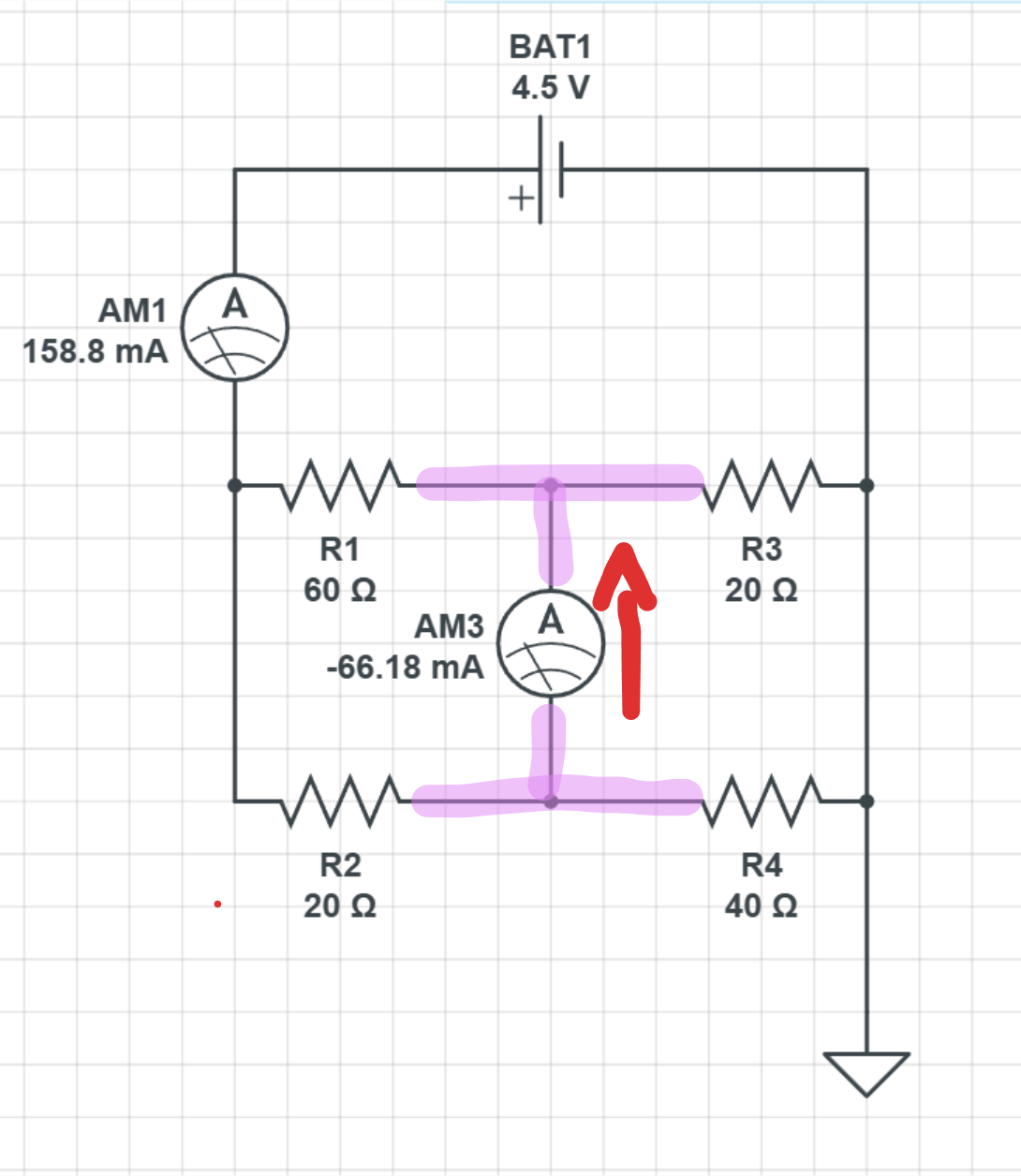
Den stora ström som kommer in via R2 kommer till största delen att lämna via R3, så det kommer att flyta en ström som bilden visar.
Jag känner när jag skriver att det här kanske inte blev någon bra förklaring alls.
Ja, det är en och samma nod. KSL håller i och med att ström in är lika med ström ut. För att det skall fungera måste strömmen gå i en viss riktning. För kretsen som helhet spelar det dock ingen roll om det är kopplat som i mina exempel eller om det är en och samma punkt.
Det finns många trådar på exakt det här temat. Här är en där jag kopplat och mätt med riktiga komponenter:
Jag brukar alltid tänka mig att kopplingarna mellan enheterna är nakna ledare och att kopplingspunkterna sker med en krokodilklämma som man bara kan glida längsmed ledaren.
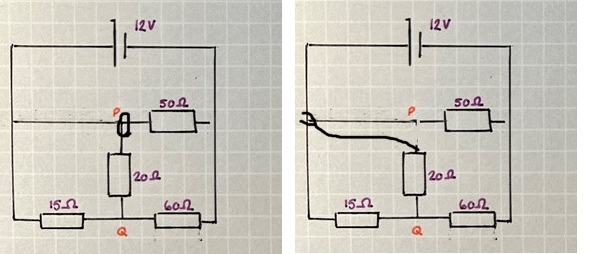
Sedan flyttar jag runt kopplingar mentalt till jag ser vilka som är parallella och vilka som är i serie.
