vad är xy

Välkommen till Pluggakuten!

Skriv om VL för den första ekvationen med hjälp av kvadreringsregeln. Hur blir det då?

Smaragdalena skrev:

Välkommen till Pluggakuten!

Skriv om VL för den första ekvationen med hjälp av kvadreringsregeln. Hur blir det då?

x^2+2xy+y^2=20

x^2+y^2=4

därför är

2xy=16

xy=8

tack, har inte ens tänkt på det

Är x och y reella tal?

Är xy = 8 i så fall möjligt, samtidigt som x^2 + y^2 = 4?

Ja...? Eller vadå?

Qetsiyah skrev:

Ja...? Eller vadå?

Ekvationssystemet går ju att lösa. Prova. 

Låt $x=r\sin(\theta),\quad y=r\cos(\theta)$ samt $x^2+y^2=r^2=4$

$xy=r^2\sin(\theta)\cos(\theta)$=8

$\sin(2\theta)=4$

Ouch.

Vadå ouch? Vem påstår vad? Jag fattar ingenting

Qetsiyah skrev:

Vadå ouch? Vem påstår vad? Jag fattar ingenting

Ouch, på så sätt att ekvationen $\sin(2\Theta)=4$ saknar lösning.

På samma sätt som ekvationssystemet

$x^2+y^2=4$

$(x+y)^2=20$

saknar (reella) lösningar:

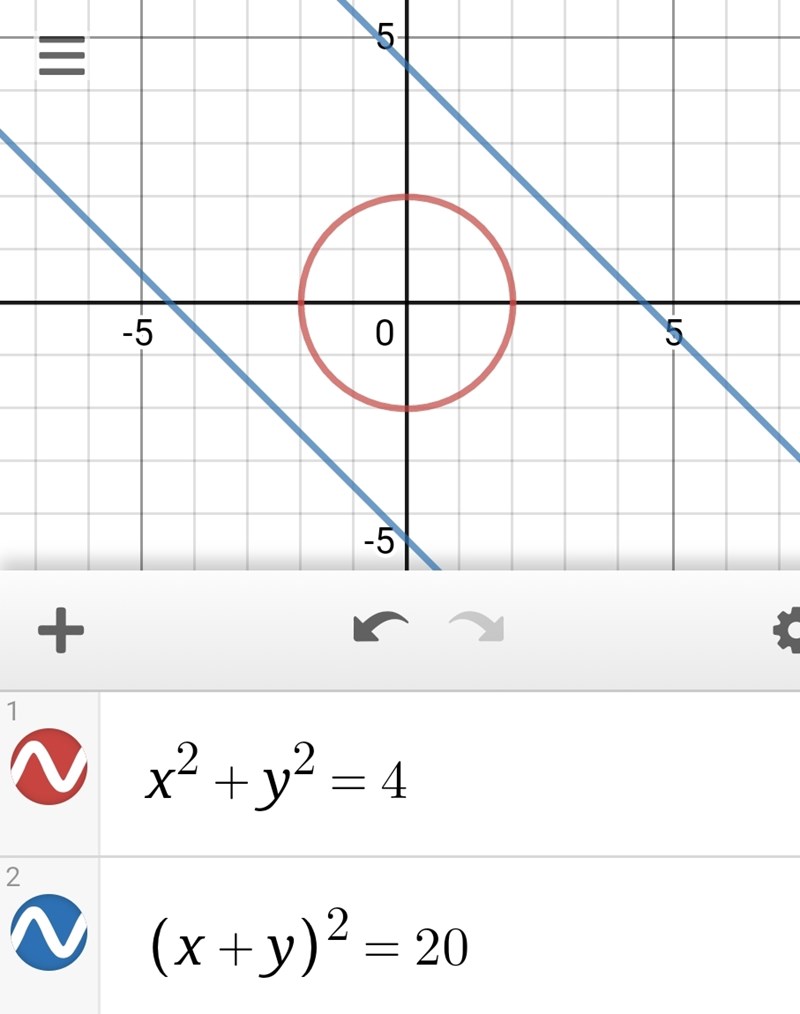
Däremot finns komplexa lösningar, men jag tror att det ligger över Matte 3 att hitta dem.

Kanske konstanterna i ekvationssystemet egentligen ska ha andra värden?

Åh ja, det såg jag inte, eller brydde mig inte snarare. Uppgiftaskaparen vill bara att man ska lära sig använda kvadreringsregeln, men det är ju en lite kul spinoff att hitta x och y

Det verkar vara en uppgift där konstruktören inte har tänkt tillräckligt långt. Intressantare än jag trodde!

Komplexa tal nämns redan i Matte 2, så då är väl uppgiften rimlig. 

Laguna skrev:

Komplexa tal nämns redan i Matte 2, så då är väl uppgiften rimlig. 

Känns som det blir en avancerad övning att bestämma $x$ och $y$. Motbevisa mig gärna om det är enkelt och på gymnasienivå.

Uppgiften är endast att bestämma värdet för xy, inte x eller y.

tomast80 skrev:

Känns som det blir en avancerad övning att bestämma $x$ och $y$. Motbevisa mig gärna om det är enkelt och på gymnasienivå.

Jo jag tyckte ovkså det, jag kan inte komma på nåt sätt spontant

Man kan bubbla på med PQ-formeln, $xy=8$ ger $y=\frac{8}{x}$

$x^4+64=4x^2$

$x_{1234}=\pm\sqrt{2\pm2i\sqrt{15}}$

Jroth skrev:

Man kan bubbla på med PQ-formeln, $xy=8$ ger $y=\frac{8}{x}$

$x^4+64=4x^2$

$x_{1234}=\pm\sqrt{2\pm2i\sqrt{15}}$

Snyggt! Vad blir lösningarna på formen:

$a+bi$ ?

Om man använder det man vet om xy kan man också få fram $(x-y)^2$.

För att hitta talen på formen a+bi kan man ha nytta en liten hjälptriangel:

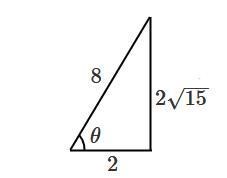
Låt oss titta på den första roten från principalgrenen $x_1=\sqrt{8}(\cos(\frac{\theta}{2})+i\sin(\frac{\theta}{2}))$. Eftersom $cos^2(\frac{\theta}{2})=\frac{1+\cos(\theta)}{2}$ och motsvarande för sinus halva vinkeln samt $\cos(\theta)=1/4$ ur hjälptriangeln 

$x_1=\sqrt{8}(\sqrt{\frac{1+\cos(\theta)}{2}}+i\sqrt{\frac{1-\cos(\theta)}{2}})=\sqrt{5}+i\sqrt{3}$.

Eftersom $y_i=\bar{x}_i$ har vi alltså avslutningsvis:

$x_1=\sqrt{5}+i\sqrt{3},\quad y_1=\sqrt{5}-i\sqrt{3}$

$x_2=\sqrt{5}-i\sqrt{3},\quad y_2=\sqrt{5}+i\sqrt{3}$

$x_3=-\sqrt{5}+i\sqrt{3},\quad y_3=-\sqrt{5}-i\sqrt{3}$

$x_4=-\sqrt{5}-i\sqrt{3},\quad y_4=-\sqrt{5}+i\sqrt{3}$

----------------------------------------------------------------------------------------------------

En alternativ lösningsgång, låt $x=z,\,y=\overline{z}$:

Eftersom (xy) $z\overline{z}=|z|^2=8$ samt $z^2+\overline{z}^2=4$ får vi med $z=a+ib$ ekvationssystemet

$a^2+b^2=8$

$a^2-b^2=2$

Lägger vi ihop den första ekvationen med den andra får vi

$2a^2=10$ och därmed $a=\pm\sqrt{5}$  samt $b=\pm\sqrt{3}$

$(x+y)^2 = 20$

$x^2+2xy+y^2 = 20$

$x^2+y^2 = 4$

$2xy = 20-4=16$

$xy = 8$

$x^2-2xy+y^2 = 4-16=-12$

$(x-y)^2 = -12$

$x+y = \pm\sqrt{20}$

$x-y = \pm i \sqrt{12}$

Osv.