Vad gör jag på uppgift 3229?
Jag provade att lösa den algebraiskt med.F(x)=ax³+bx²osv.
Suddig bild.
Står det f’(x)<0 eller f’’(x)<0?
Om det är förstaderivatan, vad betyder det att den är <0?
Det ska stå f''(x). Förlåt dålig kamera 😅
Rajt!
Om du deriverar en tredjegradsfunktion, vilken grad får derivatan då?
Alltså: ax3+bx2+cx+d, där a inte är noll.
Visa spoiler
Derivera polynomet ovan två gånger. Du får f’’(x)=6ax+2b där a inte är noll. Den måste vara negativ för tillräckligt stora positiva eller negativa x.
Det blir en andragradsfunktion och det skulle bli första derivatan
Emelie315 skrev:Det blir en andragradsfunktion och det skulle bli första derivatan
Absolut. Sedan deriverar du en gång till. Se spoilern jag precis lade till i förra svaret om du vill.
Jaha men hur blir svaret x<1?
Emelie315 skrev:Jaha men hur blir svaret x<1?
Äsch! De frågar ju om det finns några värden. Svaret är på den frågan tycker jag är ”ja, det finns det”. Får återkomma lite senare.
Låter fint :)
Du har två extrempunkter, eller hur?
Mellan dem har du en inflexionspunkt. Där är andraderivatan =0 och växlar tecken.
När f’’ < 0 så minskar grafens lutning hela tiden. Det gör den i din uppgift när x < 1. Sedan börjar den öka när x > 1.
Notera att f’ (lutningen) fortfarande är negativ efteråt, ända till min-punkten, men lutningen börjar öka.
Det är faktiskt rätt bra förklarat här: https://www.matteboken.se/lektioner/gymnasiet/matte-fortsattning-niva-1/derivatan-och-grafen/andraderivatan
Emelie315 skrev:Jag provade att lösa den algebraiskt med.F(x)=ax³+bx²osv.
Fundera först hur LUTNINGEN (tangenten, f') för kurvan ser ut för olika internvall på x-axeln. När är f'=0? (Det är den för 2 punkter. Vilka?)
Vad är lutningen till vänster om den minsta punkten och till höger om den största. Och vad är den emellan punkterna. Kan du skissa en graf? Behöver inte vara exakt, men skall visa huvuddragen.
f'' är sedan denna NYA GRAFs derivata (lutning). Har den nya grafen negativ tangent någonstans? För vilka x gäller det?
Visa spoiler
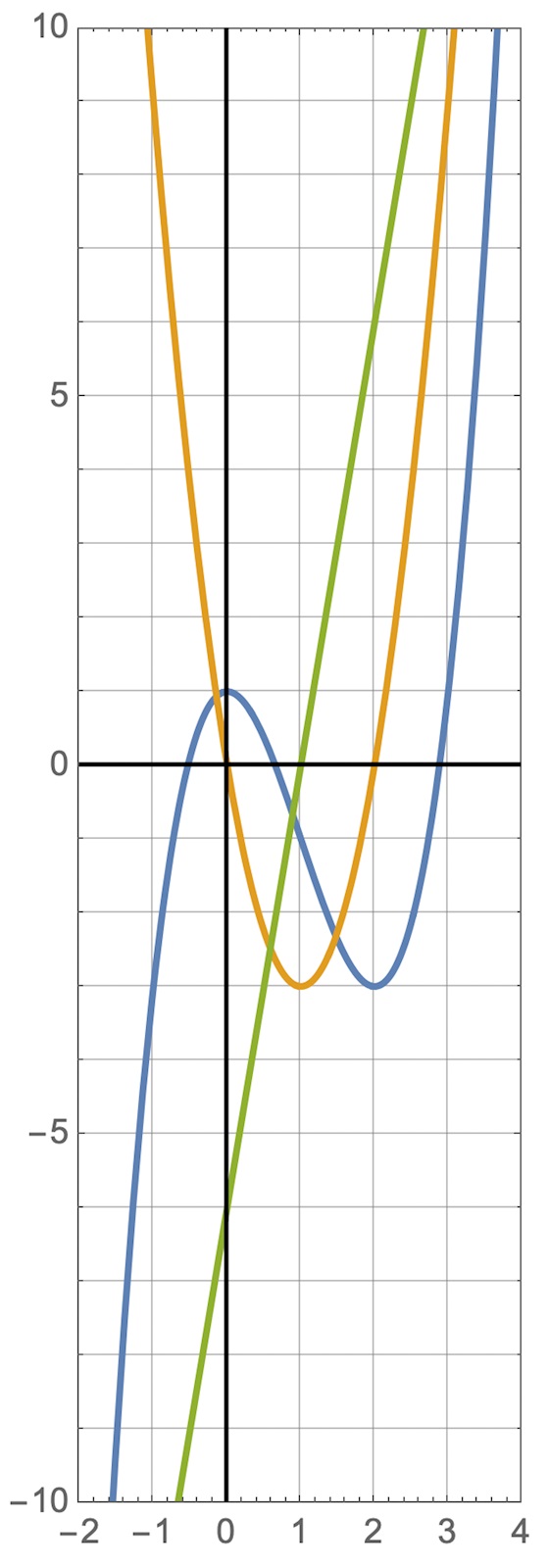
Blå = f
Gul = f'
Grön = f''

