Vad menas med räknelag?
Hej.
Går igenom basårets bok och det är lite intro om räkneregler å sånt. Min ambition är att göra alla uppgifter som mjukstart.
vad menas med räknelag? Se ned.
 mvh
mvh
Lagarna man följer vid hantering av tal kallas räknelagar. Dessa kan kännas uppenbara och onödiga i början för då har man bara sett en viss typ och det känns väldigt naturligt att man kan göra som man gör med dem.
En lag är att addition och multiplikation ger samma svar oavsett ordning:
a+b = b+a
ab=ba
Det kallas för den kommutativa lagen. Den gäller exempelvis inte när man multiplicerar något som kallas matriser. Eller när man tar kryssprodukten av två vektorer.
I ditt exempel finns det en metod man använder för samtliga uppgifter. Notera mönstret från a)-c) och använd det på det generella uttrycket a(b+c).
MrPotatohead skrev:Lagarna man följer vid hantering av tal kallas räknelagar. Dessa kan kännas uppenbara och onödiga i början för då har man bara sett en viss typ och det känns väldigt naturligt att man kan göra som man gör med dem.
En lag är att addition och multiplikation ger samma svar oavsett ordning:
a+b = b+a
ab=ba
Det kallas för den kommutativa lagen. Den gäller exempelvis inte när man multiplicerar något som kallas matriser. Eller när man tar kryssprodukten av två vektorer.
I ditt exempel finns det en metod man använder för samtliga uppgifter. Notera mönstret från a)-c) och använd det på det generella uttrycket a(b+c).
Tack för ditt svar. Du skriver "a)-c)" med bindestreck vilket alltså inkluderar b). Jag tycker att b) är en utvecklad(?) form av en faktorisering som jag kan skriva i formen:
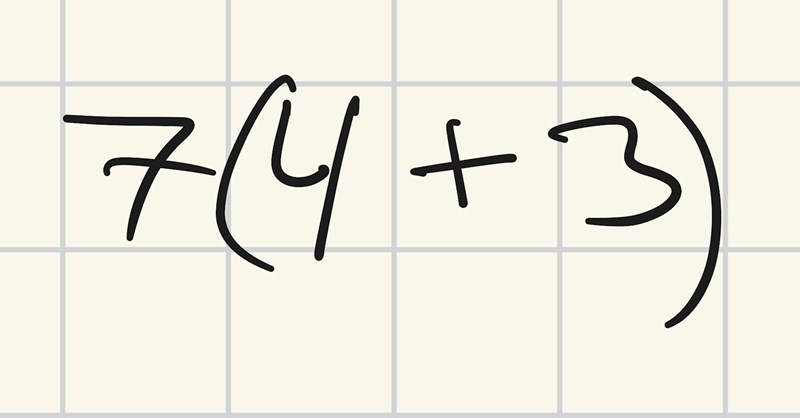
Jag ser nu att detta är a). Ska jag tolka upgiften i e) som att jag bara ska ta ett exempel på måfå som har en gemensam faktor av två termer?
Du ska fylla i högerledet med ett uttryck som innehåller a, b och c.
Laguna skrev:Du ska fylla i högerledet med ett uttryck som innehåller a, b och c.
Jahaaa. Så?😄
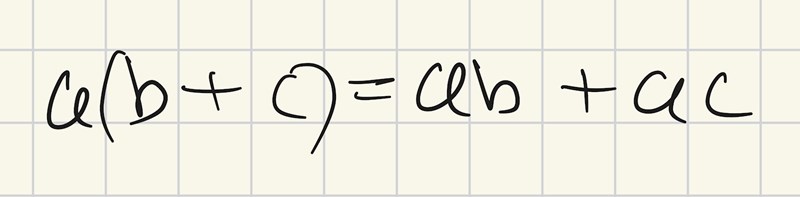
Stämmer. Ibland är jag bra seg😅. Men det är nog bra för hjärnan att programmeras in i hur det matematiska språket bör tolkas.
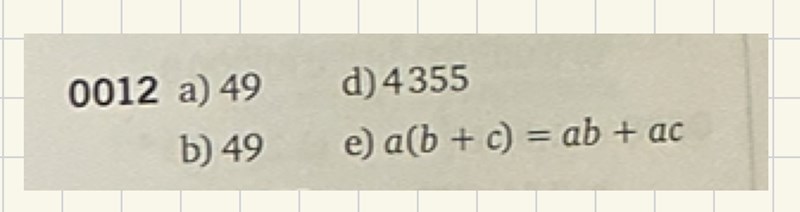
MrPotatohead skrev:Lagarna man följer vid hantering av tal kallas räknelagar. Dessa kan kännas uppenbara och onödiga i början för då har man bara sett en viss typ och det känns väldigt naturligt att man kan göra som man gör med dem.
En lag är att addition och multiplikation ger samma svar oavsett ordning:
a+b = b+a
ab=ba
Det kallas för den kommutativa lagen. Den gäller exempelvis inte när man multiplicerar något som kallas matriser. Eller när man tar kryssprodukten av två vektorer.
I ditt exempel finns det en metod man använder för samtliga uppgifter. Notera mönstret från a)-c) och använd det på det generella uttrycket a(b+c).
Och nu får dina ord en ny innebörd!😅 Älskar räknelag (alltså som det står i formelblad) för att de är lätta att memorera och nu har jag ett ord för det..




