Vad räknas som transversalsatsen?

Hej! Jag är lite förvirrad angående transversalsatsen.

Det var denna fråga som fick mig att tänka:

" I en likbent triangel dras en linje så att linjen delar triangeln i en topptriangel och ett parallelltrapets. Topptriangelns bas blir gemensam med enav sidorna i parallelltrapetset och får längden 9,0cm. Topptriangelns andra två sidor blir då 8,0 cm vardera.Beräkna längden av paralleltrapetsets sidor om topptriangeln har lika stor omkrets som paralleltrapetset."

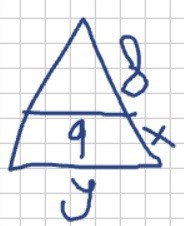
jag ställde upp två ekvationer:

y+2x+9=8+8+9

y+2x=16

(omkretsarna är likamed varandra)

topptriangelsatsen:

$\frac{C D}{A C} = \frac{D E}{A B} \frac{8}{x + 8} = \frac{9}{y} 9 x + 72 = 8 y$

$y = 16 - 2 x 8 y = 8 (16 - 2 x) 8 (16 - 2 x) = 9 x + 72 128 - 16 x = 9 x + 72 56 = 25 x x = 2, 24 y = 11.52$

det här är rätt svar, men jag vill förstå hur boken har gjort det.

Boken använder transversalsatsen, så här:

$f ö r s t p r e c i s s o m j a g : 8 + 8 + 9 = x + 9 + y + x 25 = 2 x + y + 9 m e n s e d a n s t å r d e t : " T r a n s v e r s a l s a t s e n g e r : \frac{8}{9} = \frac{8 + x}{y} (f ö r h å l l a n d e t m e l l a n m o t s v a r a n d e s i d o r) " s e d a n n l ö s e r d e b a r a e k v a t i o n s y s t e m e t$

jag trodde transversalsatsen var såhär: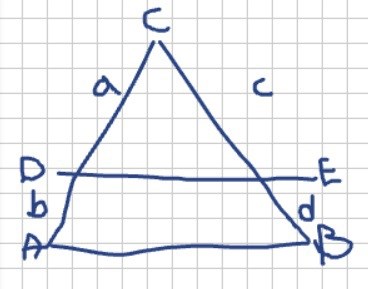

$\frac{C D}{D E} = \frac{C E}{B E} (d e t ä r d e t t a d e t s t å r i m i t t f o r m e l b l a d) m e n b o k e n g ö r a l l t s å \frac{C D}{D E} = \frac{A C}{A B} h u r k a n d e g ö r a s å ? V a d m e r f ö r s ä t t f i n n s d e t f ö r a t t a n v ä n d a t r a n s v e r s a l s a t s e n ?$

Tack för hjälpen i förhand!

Hej,

Trianglarna är likformiga. De verkar använda det om jag inte läst för snabbt.

Nej, de delar ju ena längden på botten, alltså sambandet mellan sidorna i stora triangeln är det samma som sambandet mellan sidorna i lilla toptriangeln. Är det likformighet eller transversalsatsen? Varför kallar boken det för transversalsatsen, jag håller med om att det verkar mer som likformighet eller topptriangelsatsen.

Du menar CD/DA = CE/BE för transversalsatsen.

Det är inte den satsen som boken använt. Egentligen inte topptriangelsatsen heller utan en variant av likformighet. Precis som du skriver ställer de upp att förhållandet mellan två sidor i ena triangeln är lika med motsvarande förhållande i den andra triangeln. Det är också ett sätt att ställa upp en likformighetsekvation.

Du kan se att bokens ekvation är samma som din fast omstuvad, det är samma sträckor inblandade i båda.
Och inte AD och BE som figurerar i transversalsatsen.

Transversalsatsen är inte en formel som är absolut nödvändig att kunna, man kan lika gärna använda sig av likformighet - det kan bli nägra fler steg i beviset, men om man fukar som jag så tar man gärna detta besvär för att slippa lära sig en extra formel (men å andra sidan finns ju formeln på formelbladet, och då kan ma lika gärna använda den om man känner för det).

Svara Avbryt

Visa senaste svar