Vågfysik, interferens
Hej! Har suttit och klurat på den här uppgiften hur länge som helst och får verkligen inte till den.
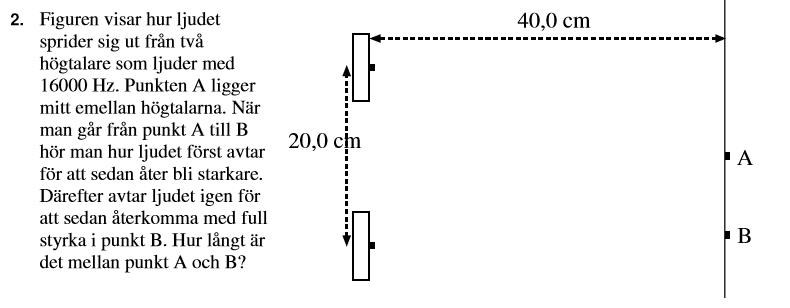
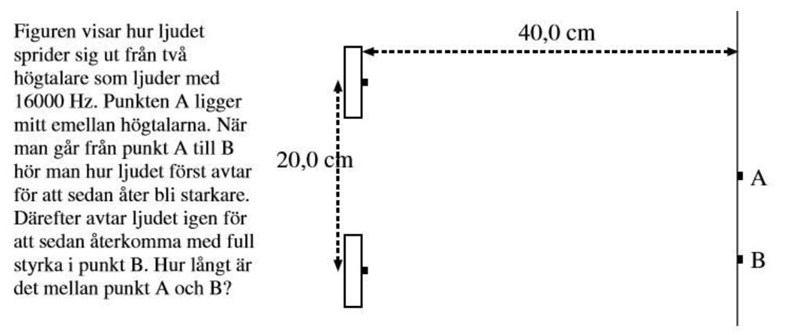
Figuren visar hur ljudet sprider sig ut från två högtalare som ljuder med 16000 Hz. Punkten A ligger mitt emellan högtalarna. När man går från punkt A till B hör man hur ljudet först avtar för att sedan åter bli starkare. Därefter avtar ljudet igen för att sedan återkomma med full styrka i punkt B. Hur långt är det mellan punkt A och B?
Går inte att bifoga bilden men längden mellan högtalarna och linjen där punkt A & B finns är 40 cm och det är 20 cm mellan de två högtalarna. Den finns även på sida 4 av länken nedan! Problem 2 på B uppgifterna.
https://fysikstugan.se/wp-content/uploads/2019/03/Vågfysik-Mekaniska-vågor-Fysik-2.pdf
Förstår att det är 2 våglängder mellan A & B men kommer verkligen inte längre än så. Har försökt ställa upp trianglar och räkna på det viset men eftersom B inte ligger direkt framför den andra högtalaren så blir det inte en rätvinklig triangel. Tacksam för all hjälp!!
I facit står det: 11,4 cm (punkten A ligger mitt emellan högtalarna)
Det finns väl en anledning till att ingen svarar på din tråd.
Det är väl inte meningen att man först ska lösa någon slags rebus, för att kunna hjälpa dig med din uppgift?
Jag har också fastnat på denna uppgift.
Jag anser att punkt B ligger vid andra ordningens maximum, dvs skillnaden i sträcka som ljudet från de två högtalarna färdas till punkt B är 2 våglängder.
Våglängden = v/f = 340/16000 m = 0.02125 m.
Med hjälp av formlerna i bilden nedan ( med L=0.4m, d=0.2m, delta r=2 våglängder m) får jag y, dvs avståndet mellan punkt A och B till 0.087 m.
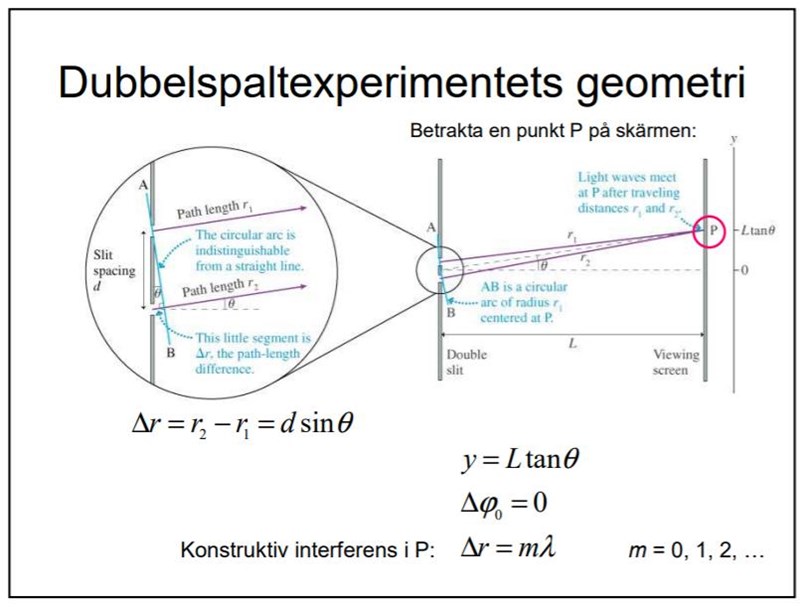
På vilket sätt tänker jag fel? Eller kan facit ange fel svar? :-S
De figurer och formler ni hänvisar till, tycks innehålla antaganden som leder till felaktiga approximationer.
Prova i stället med att tillämpa Pythagoras på nedanstående två trianglar...
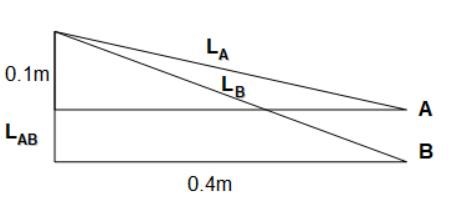
Får ut längden LA till 0,412 med
Då borde LB bli om LAB är längden mellan punkt A & punkt B
Men eftersom man varken har LB eller LAB så förstår jag inte hur man ska få ut något svar, kanske har kollat på uppgiften för länge och inte ser något som är uppenbart men har kört fast
...andra maxima...
Försök låta bli att beräkna några avrundade mellanresultat! Skriv då tills vidare t.ex.
Använd bokstavsekvationer tills du har:
Äntligen fick jag till det!! Tack så jättemycket för hjälpen, förstod också vart jag hade tänkt fel. Fick för mig att men det är ju !
Kan man utgå från att LB - LA = 2? (Namn från Affe Jkpgs bild)
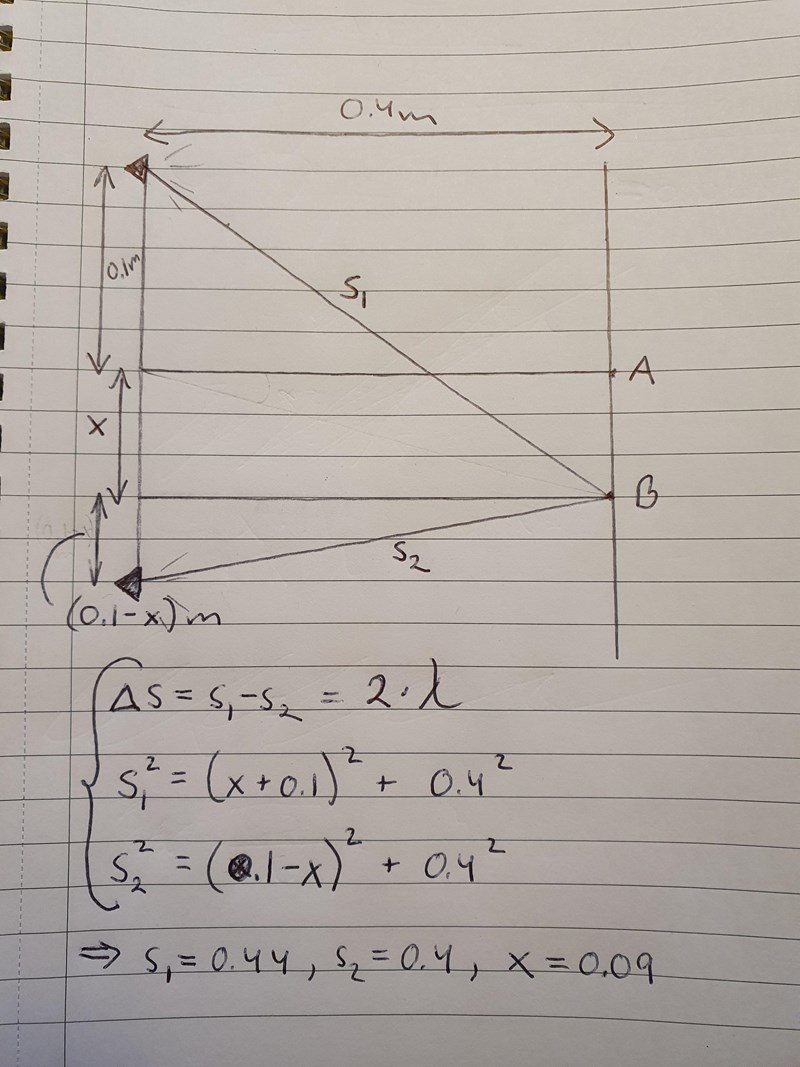
Det är längdskillnaden mellan sträckorna till punkt B från de två högtalarna som är 2 som jag förstår teorin, dvs S1 - S2 = 2, se min bild nedan. Jag får avståndet mellan punkt A och B till 0.09 m vid lösning av ekvationssystemet i bilden nedan.
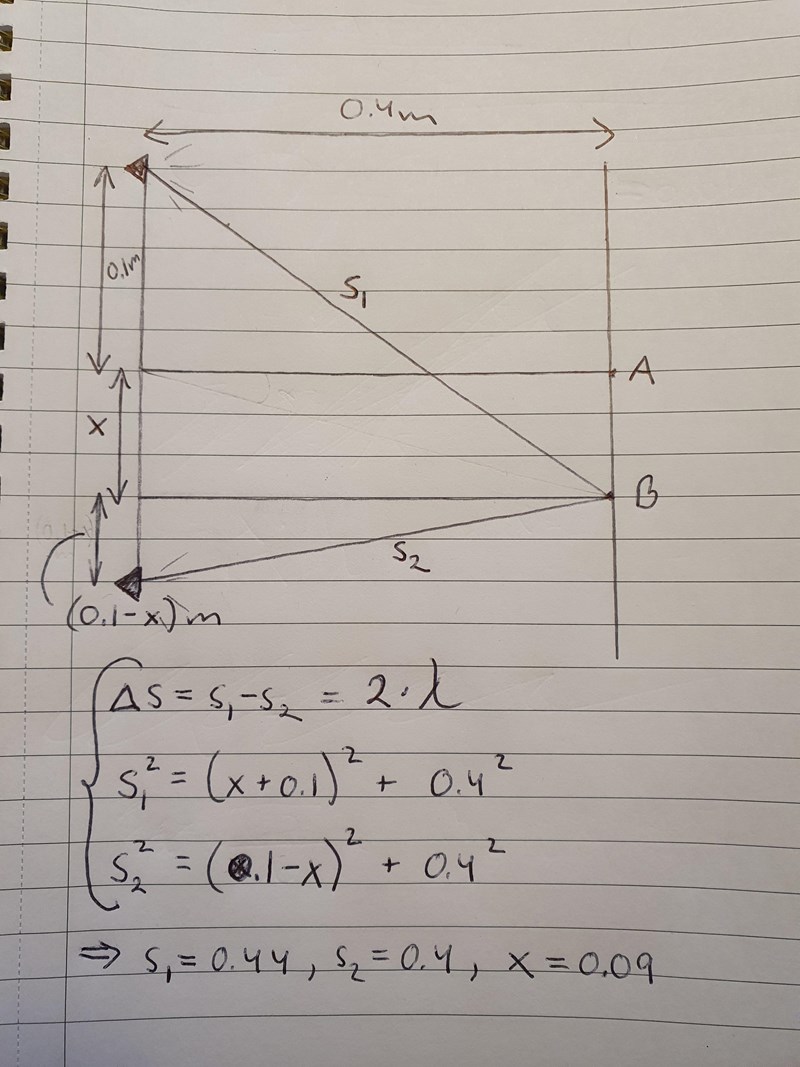
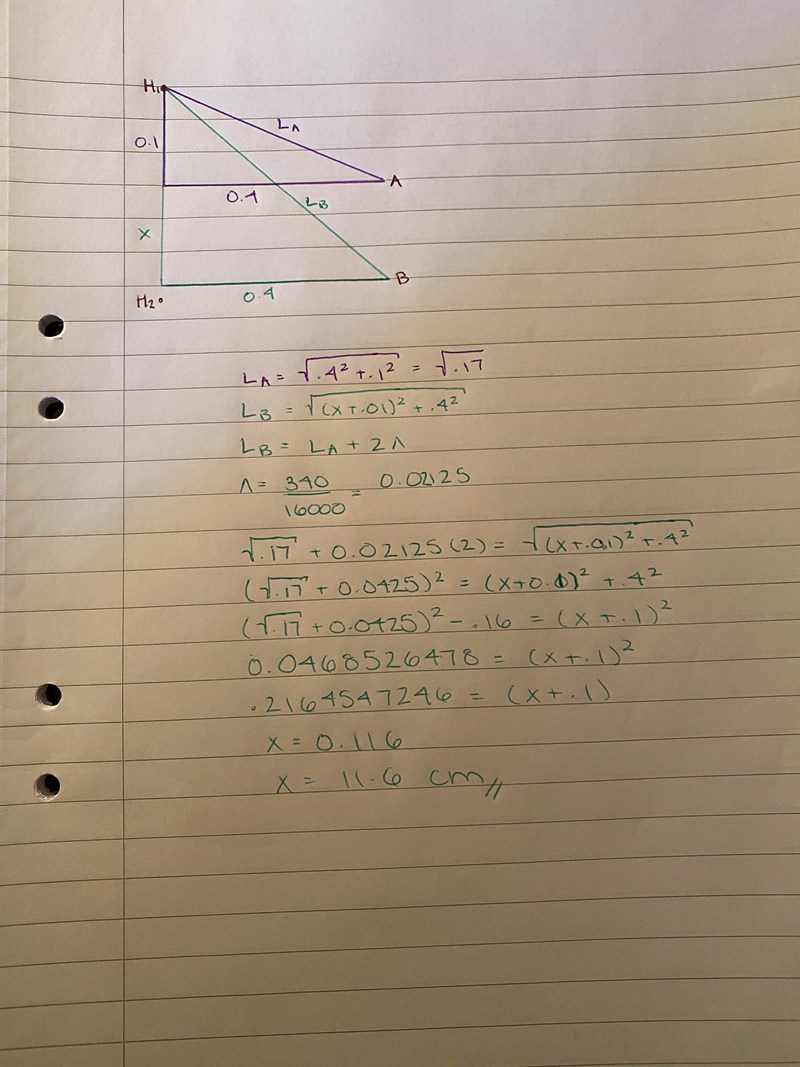
Eftersom man inte vet längden på eller
Tack för din beräkning felicia7. Jag är med på hur du räknar. Det är antagandet om att LB - LA = λ2 som jag är frågande till.
Det är antagandet om att LB - LA = 2λ som jag är frågande till.
Läs uppgiften om vad som händer när man går från A till B.
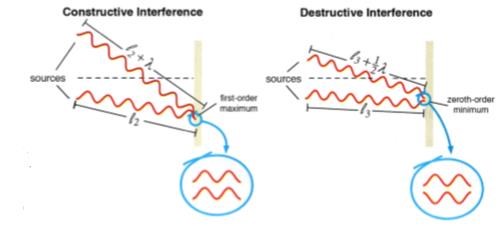
Jag håller med. Din bild om interferens mellan två källor visar på att man ska kika på sträckorna från respektive ljudkälla till en punkt med maximum och längdskillnaden är där n våglängder, n anger maximumets ordning. I detta fall är det andra ordningens maximum och således är vägskillnaden 2 våglängder.
I din tidigare bild tipsar du om att vägskillnaden för sträckorna från den ena ljudkällan till två punkter med maximum är 2 våglängder vilket jag ej förstår och envist undrar över.
I din tidigare bild tipsar du om att vägskillnaden för sträckorna från den ena ljudkällan till två punkter med maximum är 2 våglängder vilket jag ej förstår och envist undrar över.
Jaha, vad sägs om nedanstående illustration, som ett tillägg till illustrationen med de två trianglarna:
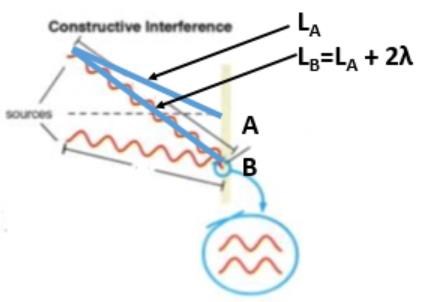
Tack för ytterligare förklaring. Dock håller jag ändå inte med. :)
Juniverse skrev:Tack för ytterligare förklaring. Dock håller jag ändå inte med. :)
Vad är det du inte håller med om?
Jag kan förstås vara ute och cykla, men jag hittar ingen teori om att vägskillnaden från en ljudkälla till två maximum skulle vara ett jämnt antal våglängder.
Juniverse skrev:Jag kan förstås vara ute och cykla, men jag hittar ingen teori om att vägskillnaden från en ljudkälla till två maximum skulle vara ett jämnt antal våglängder.
Vad menar du med det? Slå upp konstruktiv interferens! När händer detta? När vågorna förstärker varandra. Om de gör detta vid ett maximum, vad är då vägskillnaden mellan vågorna?
Sök på youtube på "Konstruktiv interferens" eller "Constructive interference".
Affe Jkpg skrev:I din tidigare bild tipsar du om att vägskillnaden för sträckorna från den ena ljudkällan till två punkter med maximum är 2 våglängder vilket jag ej förstår och envist undrar över.
Jaha, vad sägs om nedanstående illustration, som ett tillägg till illustrationen med de två trianglarna:
Jag kan förstås vara ute och cykla, men jag hittar ingen teori om att vägskillnaden från en ljudkälla till två maximum skulle vara ett jämnt antal våglängder.
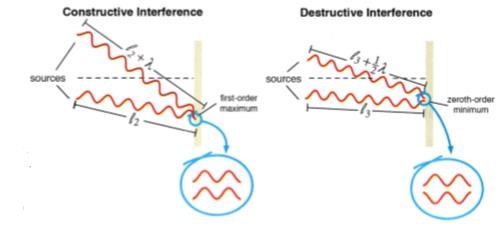
Den lilla inringade delen av bilden, illustrerar konstruktiv (samverkande) interferens.
Det är konstruktiv interferens mellan ljudvågorna från högtalare 1 och högtalare 2 och i maximumet av andra graden är vägskillnaden 2 våglängder.
Ni hävdar att ljudvågorna från enbart högtalare 1 har vägskillnaden 2 våglängder. Detta är jag inte med på.
Ni hävdar att ljudvågorna från enbart högtalare 1 har vägskillnaden 2 våglängder. Detta är jag inte med på.
Nej, vi påstår att det är vägskillnaden mellan högtalare 1 och högtalare 2 är 2 våglängder. En vägskillnad kan inte bero på bara vågorna från en enda högtalare.
Men i tidigare bild anges där och är sträckorna från högtalare 1.
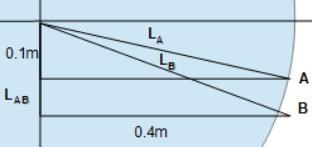
LA är avståndet från den undre högtalaren till "mötesplatsen", men parallellförflyttat i ett tydligen fåfängt försök att vara tydlig och inte skriva allting ovanpå varandra.
Kan du vara snäll och förtydliga din senaste kommentar med en bild?
Här är bilden:
Det är ju samma bild som tidigare där LB−LA= 2λ, LA och LB är sträckorna från den övre högtalaren. Jag förstår fortfarande hur man kan säga att LB-LA=2λ då LA och LB kommer från samma källa?
Affe har ritat in en blå linje som är parallell med den nedersta våglinjen. Har du aldrig sett att man markerar längden för en linje med en parallell linje? Meningen är att man skall visa längden utan att kladda allt på samma ställe.
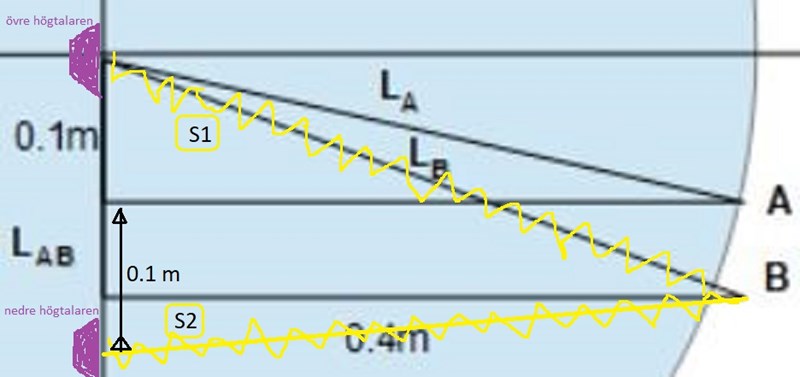
Nu har jag i bakgrunden (blått) ritat en ljudvåg som kommer från översta högtalaren.
Den har nått punkten A men har en bit kvar () till punkten B.
Jag ser det enligt bilden nedan. S1-S2=2. S2.
Kan du lägga in en bild från din ursprungliga uppgift här i tråden, så att vi kan veta att vi pratar om samma sak? Jag trodde att Affe hade lagt in just din uppgift i sitt första inlägg, men om det inte är rätt bild kan du väl lägga in den?!
Juniverse skrev:Jag ser det enligt bilden nedan. S1-S2=2. S2.
Det är en uppmärksam iaktagelse du gör!
Att det uppstår konstruktiv interferens i punkten B är en iaktagelse av vad som händer när man går från A till B. Därför bör man kunna avstå ifrån att betrakta längden av vägsträckan mellan undre högtalaren och punkten B, annat än som en konsekvens av konstruktiv interferens mellan övre högtalaren och punkten B.
Förstår tyvärr inte din, Affe, förklaring varför man bör kunna avstå från att betrakta längden av vägsträckan mellan undre högtalaren och punkten B?
Den ursprungliga uppgiften:
Förstår tyvärr inte din, Affe, förklaring varför man bör kunna avstå från att betrakta längden av vägsträckan mellan undre högtalaren och punkten B?
Man kan roa sig med att rita en ny triangel med utgångspunkt från din undre gula linje och en horisontell linje ut till punkten B. Sedan får man se om man kommer till samma slutsats om svaret på uppgiften :-)
Det gjorde jag i min lösning tidigare. Jag får ut att sträckan är 0.0895 m 0.09 m. Ekvationslösningen har jag fått med hjälp av Geogebra.
Dock anger facit tydligen svaret 11.4 cm enligt felicia7 som startade denna tråd. Min ursprungliga fråga var om facit var fel för denna uppgift. Vad får ni för svar?
Min uppställning igen:
Juniverse skrev:Det gjorde jag i min lösning tidigare. Jag får ut att sträckan är 0.0895 m 0.09 m. Ekvationslösningen har jag fått med hjälp av Geogebra.
Dock anger facit tydligen svaret 11.4 cm enligt felicia7 som startade denna tråd. Min ursprungliga fråga var om facit var fel för denna uppgift. Vad får ni för svar?
Min uppställning igen:
Man kan hålla reda på antalet värdesiffror och bl.a. svara med 9.0cm
Bra jobbat Juniverse!
Tack!
Kan jag utgå från att facits svar 11.4 cm är fel?




