Vågrörelselära/Emittans - Cylinder i omloppsbana till solen

Jag hittade en uppgift om emittans här på pluggakuten, länk till uppgift;https://www.pluggakuten.se/trad/emittans/. Till denna uppgift finns det en uppgift på en cylinder som rör sig i en omloppsbana runt solen vilket gör att den utsätts för emittans på den arean som blir belyst. 

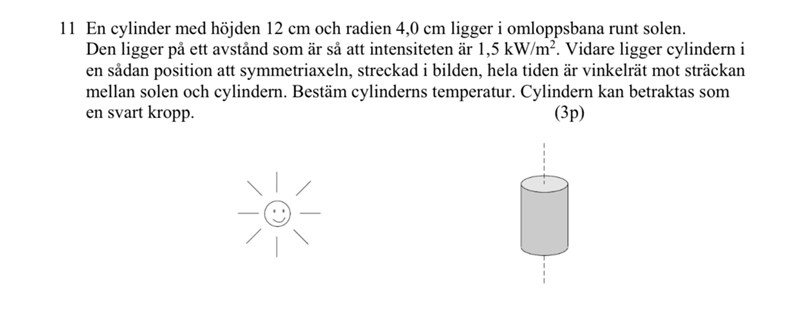
Jag läste det som stod i kommentarsfältet och provade på att lösa uppgiften själv. Det här är min lösning i korta drag.

Först av allt har vi själva cylindern som tar in värme genom effekten från emittans. Effekten som kommer in är lika stor som den som förloras, dvs $P_{In} = P_{Ut}$

$M_{In} = \frac{P_{In}}{A_{In}} \to P_{In} = M_{In}{A}_{In}$

$M_{Ut} = \frac{P_{Ut}}{A_{Ut}} \to P_{Ut} = M{A}_{Ut} \to P_{Ut} = \sigma \cancel{\epsilon }{T}^4{A}_{Ut}$

$\sigma T^4{A}_{Ut} = M_{In}{A}_{In} \to T = \sqrt[4]{\frac{M_{In}}{\sigma }\frac{A_{In}}{A_{Ut}}}$

Därefter måste man bestämma areorna. För arean ut så gäller det den totala arean som cylindern har dvs $A_{Ut} = 2\pi rh + 2\pi r^2$

Men för arean som värms upp av emittans så blir det cirkelsektorn av vinkeln där cylindern blir belyst gånger vinkeln för det. Jag valde att illustrera detta i samband med solen, som jag tolkar som en punkt som utsöndrar energi genom effekt. Man kan tänka att man ser ned på cylindern ovanifrån, så att man får en bättre bild på denna cirkelsektor jag pratar om.

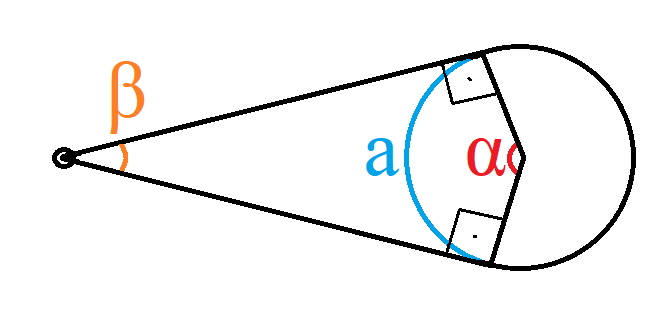
Här är $a$ cirkelsektorn och vinklarna $\alpha , \beta$ är de två vinklarna i denna triangelliknande fyrhörning. Det finns två räta vinklar vilket summeras till $\pi$ radianer då hela figurens ekvation blir till $\alpha + \beta + \pi = 2\pi \to \alpha = \pi - \beta$

Saken är att jag inte kan bestämma $\alpha$. Eller inte genom denna ekvation även om den beskriver med hur stor vinkel cylindern borde belysas. Mitt antagande är då att $\beta$ närmar sig 0 då $\alpha = \pi$, fast detta måste man bara helt enkelt anta vilket jag skulle gissa är det enda man kan göra utifrån den information jag fick.

Då blir den belysta arean följande, $A_{In} = \mathrm{\pi rh}$

Då blir den slutgiltiga lösningen såhär; $T = \sqrt[4]{\frac{M_{In}}{\sigma }\frac{\pi rh}{2\pi rh+2\pi r^2}} \to T = \sqrt[4]{\frac{M_{In}}{\sigma }\frac{h}{2(h+r)}}$

Och själva uträkningen blir då; $T = \sqrt[4]{\frac{M_{In}}{\sigma }\frac{2(h+r)}{h}} \to T = \sqrt[4]{\frac{1.5·{10}^3}{5.67·{10}^{-8}}\frac{12}{2(12+4)}} \to T = 315.59 \left[K\right]$

Jag hoppas att min uträkning stämmer och ifall jag gjorde något fel i uträkningen mm. Och ifall någon har facit så skulle jag vara väldigt tacksam att få se vad det riktiga svaret skulle bli. Tack!