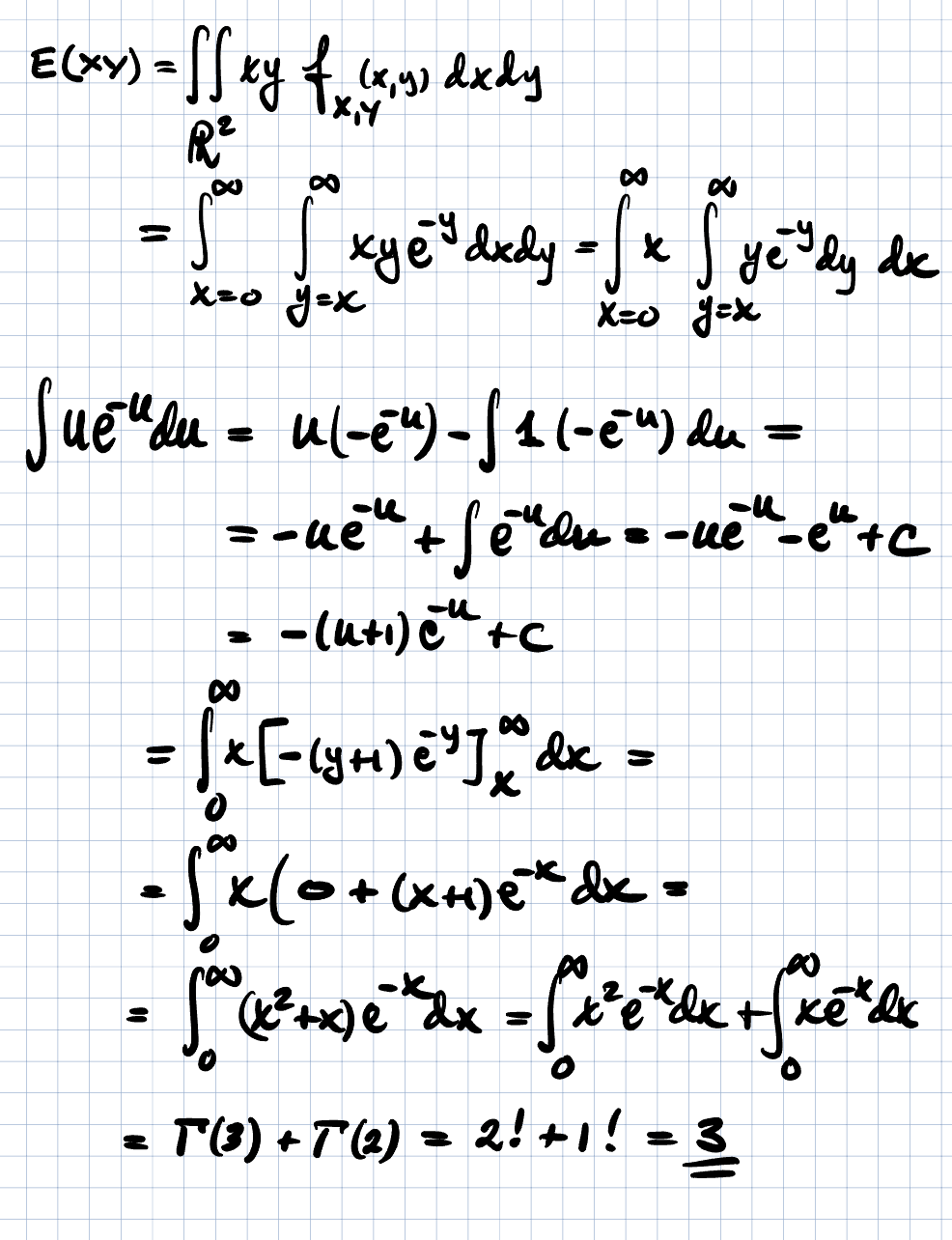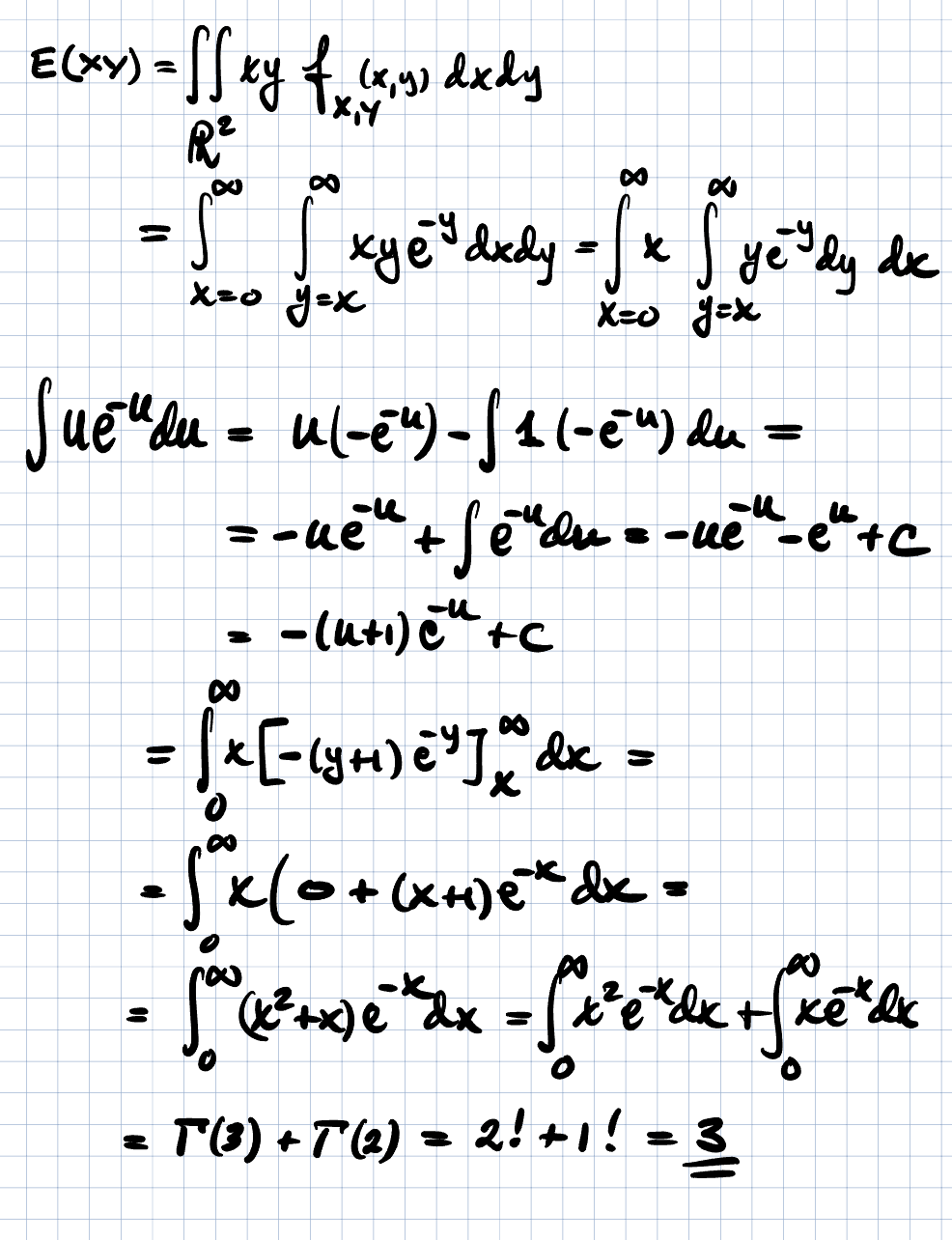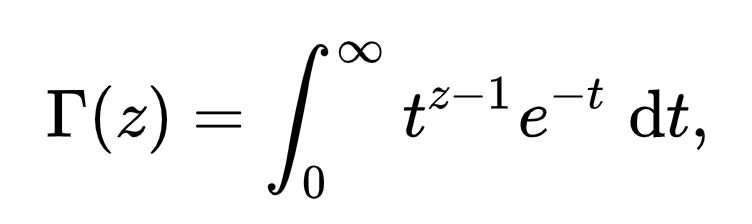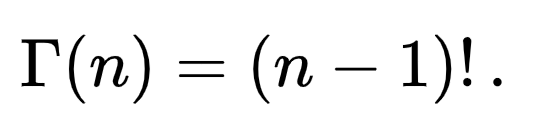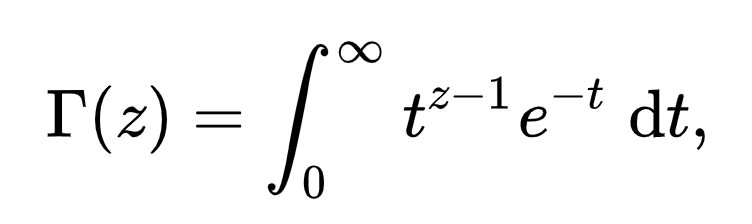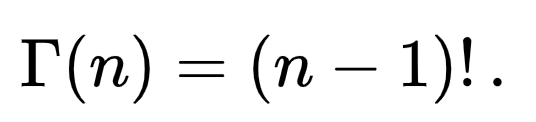Väntevärdet E(XY)

Dubbelintegral med

x y f_{X,Y}(x,y)

som integrand över R2 som blir "begränsat" då f=0 för stor del av R2.

(Det blir en 45°-ig sektor i 1:a kvadranten.)

Trinity2 skrev:

Dubbelintegral med

x y f_{X,Y}(x,y)

som integrand över R2 som blir "begränsat" då f=0 för stor del av R2.

(Det blir en 45°-ig sektor i 1:a kvadranten.)

Hm jag hänger inte gällande 45 grader i 1:a kvadranten. Men menar du något sånt här typ? Se bild nedan:

x=0..oo

y=x..oo

Trinity2 skrev:

x=0..oo

y=x..oo

Hm varför varierar x mellan 0 till oo och x till oo?

destiny99 skrev:

Trinity2 skrev:

x=0..oo

y=x..oo

Hm varför varierar x mellan 0 till oo och x till oo?

Har du skissat området i R2?

Trinity2 skrev:

destiny99 skrev:

Visa föregående citat

Trinity2 skrev:

x=0..oo

y=x..oo

Hm varför varierar x mellan 0 till oo och x till oo?

Har du skissat området i R2?

Det blir ju en sådan figur, dock kan jag inte få till oo. 

Jag får typ ett jättekonstigt uttryck som inte är ett värde när jag löser på det sättet. 

Trinity2 skrev:

Jag vet inte vad du gör på slutet där , men kan man inte köra vanliga 2 ggr partiell integration för termen x^2e^-x dx ? Jag antar att svaret blir samma.

Det kan du göra men studera gärna (inte allt, bara delar) 

https://en.wikipedia.org/wiki/Gamma_function

så spar du mycket tid på prov.

Trinity2 skrev:

Det kan du göra men studera gärna (inte allt, bara delar) 

https://en.wikipedia.org/wiki/Gamma_function

så spar du mycket tid på prov.

Ja jag förstår. Men detta använde inte facit och jag är osäker på om det lärs ut iom att jag inte känner igen den val av metoden.

Tillägg: 8 jul 2025 23:23

Edit: jag hittade den i vår formelsamling men jag har aldrig jobbat med den. Får lära mig hur det fungerar. 

destiny99 skrev:

Trinity2 skrev:

Det kan du göra men studera gärna (inte allt, bara delar) 

https://en.wikipedia.org/wiki/Gamma_function

så spar du mycket tid på prov.

Ja jag förstår. Men detta använde inte facit och jag är osäker på om det lärs ut iom att jag inte känner igen den val av metoden.

Det är en bra övning i Analys1 att bevisa att integralen är n!

Halvt relaterat, men en annan trevlig släkting till gammafunktionen är betafunktionen:

$\displaystyle  B\left(x,y\right) = \int_0^1 t^{x-1}\left(1-t\right)^{y-1} \mathrm dt$

Man kan visa att 

$\displaystyle  B\left(x, y\right) = \frac{\Gamma\left(x\right)\Gamma\left(y\right)}{\Gamma\left(x+y\right)}$

Och då för positiva heltal $n,m$ 

$\displaystyle B\left(n, m\right) = \frac{(n-1)!(m-1)!}{(n+m-1)!}$

Förhållandet mellan gamma- och betafunktionen är lite knepigare att visa, men mycket mycket användbart (min favorit är att ta derivatan av betafunktionen för att få fram intressanta integraler)! Särskilt med alla olika representationer för beta funktionen som finns. 

destiny99 skrev:

Jag får typ ett jättekonstigt uttryck som inte är ett värde när jag löser på det sättet. 

Examinatorn anser att det är felaktigt uppställd för E(XY) på rad 2 , men allt annat fram till svaret är korrekt. Ska man inte ställa upp som jag gjort eller är det mer korrekt att skriva R^2 som trinity gjorde? Sen undrar jag varför man skriver R^2?