Värdemängd, mängdlära
En annan fråga
Låt f : [0, ∞[→ R vara funktionen definierat genom f(x) = x^2 + 4x + 3
* Beräkna f(0) och f ◦ f(0).
* Bestäm värdemängden Vf
till f .
*Visa a f är injektiv
Första hänger jag med
Man sätter först in 0 i ekvationen och får svar 3
Sedan sätter man 3 i ekvationen och får svar 24
Men hur gör man:
* Bestäm värdemängden Vf
till f .
Vet att detta har med y värden att göra
och hur visar man att den är injektiv?
Standardfråga 1a: Har du ritat?
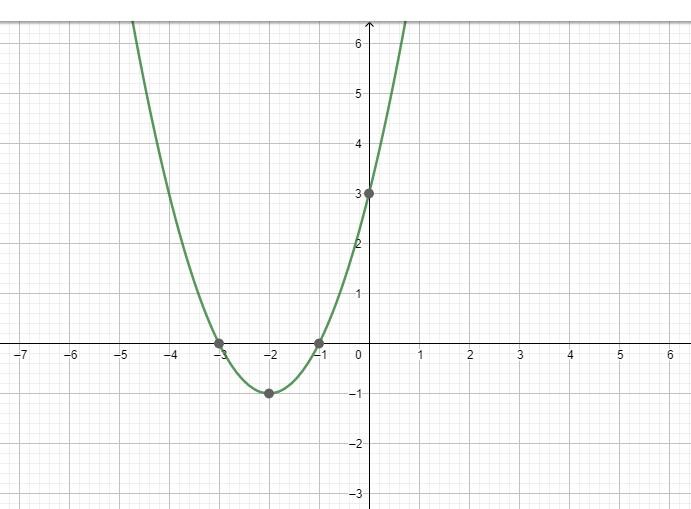
Eftersom du har en andragradsfunktion kan du enklare se värdemängden om du kvadratkompletterar funktionens uttryck.
Jo har ritat och ser att jag får x= 3,-1,-3 och y =-2
Men hänger ej med vad man ska få ut av grafen?
Sedan kan man köra pq formel för att få värdemängden?
Malisan74 skrev:Jo har ritat och ser att jag får x= 3,-1,-3 och y =-2
Men hänger ej med vad man ska få ut av grafen?
Sedan kan man köra pq formel för att få värdemängden?
Vad menar du med "x= 3,-1,-3 och y =-2"?
pq-formeln kan du använda för att få veta de viktiga egenskaperna som funktionen har, och att rita hjälper till att se om man gör rätt och tittar på rätt saker. Vilket är det minsta värde som f kan anta? Är värdena begränsade uppåt?
När du har fått fram värdemängden är det dags att svara på frågan om f är injektiv.
När man ritar grafen är det dom skärpunkterna grafen får
Men hänger ej med riktigt på vad ni menar
Jo har ritat och ser att jag får x= 3,-1,-3 och y =-2
Kan du ta ett foto av det du ritat och lägga in din bild här? Jag förstår inte vad du menar med det du har skrivit.
Att rita upp en andragradsfunktion och beräkna dess nollställern lär man sig i Ma2, så eftersom du har lagt den här uppgiften i Matematik/Universitet borde det vara en självklarhet för dig. Om du saknar de grundkunskaper i matematik som du förväntas ha när du studerar universitetsmatte kommer du att få det förfärligt jobbigt.
Vilket är det minsta värde på f(x) du kan få, om du stoppar in alla tillåtna x-värden?
Vilket är det största värde på f(x) du kan få, om du stoppar in alla tillåtna x-värden?
Vilken är värdemängden?
Malisan74 skrev:När man ritar grafen är det dom skärpunkterna grafen får
Men hänger ej med riktigt på vad ni menar
Jag begriper fortfarande inte alls vad "x= 3,-1,-3 och y =-2" betyder. y är aldrig -2.
Smaragdalena skrev:Vilket är det minsta värde på f(x) du kan få, om du stoppar in alla tillåtna x-värden?
Vilket är det största värde på f(x) du kan få, om du stoppar in alla tillåtna x-värden?
Vilken är värdemängden?
Förmodar att man ska stoppa in -1 och -3?
Laguna skrev:Malisan74 skrev:När man ritar grafen är det dom skärpunkterna grafen får
Men hänger ej med riktigt på vad ni menar
Jag begriper fortfarande inte alls vad "x= 3,-1,-3 och y =-2" betyder. y är aldrig -2.
Nollställen men skrev fel på -2
Din graf stämmer inte riktigt. Funktionen är endast definierad för .
I det området (dvs på och till höger om y-axeln):
- Finns det något lägsta värde som y antar? I så fall vilket?
- Finns det något högsta värde som y antar? I så fall vilket?
- Finns det något värde mellan dessa som y inte antar? I så fall vilket/vilka?
Yngve skrev:Din graf stämmer inte riktigt. Funktionen är endast definierad för .
I det området (dvs på och till höger om y-axeln):
- Finns det något lägsta värde som y antar? I så fall vilket?
- Finns det något högsta värde som y antar? I så fall vilket?
- Finns det något värde mellan dessa som y inte antar? I så fall vilket/vilka?
Kan man på något sätt matematiskt räkna ut detta?
Malisan74 skrev:En annan fråga
Låt f : [0, ∞[→ R vara funktionen definierat genom f(x) = x^2 + 4x + 3
* Beräkna f(0) och f ◦ f(0).
* Bestäm värdemängden Vf
till f .*Visa a f är injektiv
Första hänger jag med
Man sätter först in 0 i ekvationen och får svar 3
Sedan sätter man 3 i ekvationen och får svar 24
Men hur gör man:
* Bestäm värdemängden Vf
till f .Vet att detta har med y värden att göra
och hur visar man att den är injektiv?
Är första beräkningen rätt? Svar 3 och 24? dvs * Beräkna f(0) och f ◦ f(0).
Malisan74 skrev:Yngve skrev:Din graf stämmer inte riktigt. Funktionen är endast definierad för .
I det området (dvs på och till höger om y-axeln):
- Finns det något lägsta värde som y antar? I så fall vilket?
- Finns det något högsta värde som y antar? I så fall vilket?
- Finns det något värde mellan dessa som y inte antar? I så fall vilket/vilka?
Kan man på något sätt matematiskt räkna ut detta?
Inte omöjligt, men det enklaste och bästa sättet är att titta på bilden.
Malisan74 skrev:Malisan74 skrev:En annan fråga
Låt f : [0, ∞[→ R vara funktionen definierat genom f(x) = x^2 + 4x + 3
* Beräkna f(0) och f ◦ f(0).
* Bestäm värdemängden Vf
till f .*Visa a f är injektiv
Första hänger jag med
Man sätter först in 0 i ekvationen och får svar 3
Sedan sätter man 3 i ekvationen och får svar 24
Men hur gör man:
* Bestäm värdemängden Vf
till f .Vet att detta har med y värden att göra
och hur visar man att den är injektiv?
Är första beräkningen rätt? Svar 3 och 24? dvs * Beräkna f(0) och f ◦ f(0).
f(0) = 3, det stämmer.
Men jag vet inte vad f ° f(0) avser.
Antagligen menas den sammansatta funktionen f(f(0)). Då stämmer svaret 24.
Men jag har för mig att en sådan sammansatt funktion brukar betecknas (f°f)(x).
Smaragdalena skrev:Malisan74 skrev:Yngve skrev:Din graf stämmer inte riktigt. Funktionen är endast definierad för .
I det området (dvs på och till höger om y-axeln):
- Finns det något lägsta värde som y antar? I så fall vilket?
- Finns det något högsta värde som y antar? I så fall vilket?
- Finns det något värde mellan dessa som y inte antar? I så fall vilket/vilka?
Kan man på något sätt matematiskt räkna ut detta?
Inte omöjligt, men det enklaste och bästa sättet är att titta på bilden.
Borde vara -1 till 3?
Malisan74 skrev:
Borde vara -1 till 3?
Nej funktionen antar inte värdet -1 någonstans i sin definitionsmängd. Definitionsmängden är alla .
Negativa värden på x ingår inte i definitionsmängden.
Malisan74 skrev:Smaragdalena skrev:Malisan74 skrev:Yngve skrev:Din graf stämmer inte riktigt. Funktionen är endast definierad för .
I det området (dvs på och till höger om y-axeln):
- Finns det något lägsta värde som y antar? I så fall vilket?
- Finns det något högsta värde som y antar? I så fall vilket?
- Finns det något värde mellan dessa som y inte antar? I så fall vilket/vilka?
Kan man på något sätt matematiskt räkna ut detta?
Inte omöjligt, men det enklaste och bästa sättet är att titta på bilden.
Borde vara -1 till 3?
Nej.
Titta på bilden. Eftersom definitionsmängden för f(x) är från och med 0 och uppåt, är det bara den del av kurvan som ligger på eller till höger om y-axeln som är intressanta. Ser du att ju mer du flyttar dig åt höger, desto större blir värdet av f(x)? Man säger att fuktionen är växande. Vilket är det minsta "godkända" värdet för f(x)?
Smaragdalena skrev:Malisan74 skrev:Smaragdalena skrev:Malisan74 skrev:Yngve skrev:Din graf stämmer inte riktigt. Funktionen är endast definierad för .
I det området (dvs på och till höger om y-axeln):
- Finns det något lägsta värde som y antar? I så fall vilket?
- Finns det något högsta värde som y antar? I så fall vilket?
- Finns det något värde mellan dessa som y inte antar? I så fall vilket/vilka?
Kan man på något sätt matematiskt räkna ut detta?
Inte omöjligt, men det enklaste och bästa sättet är att titta på bilden.
Borde vara -1 till 3?
Nej.
Titta på bilden. Eftersom definitionsmängden för f(x) är från och med 0 och uppåt, är det bara den del av kurvan som ligger på eller till höger om y-axeln som är intressanta. Ser du att ju mer du flyttar dig åt höger, desto större blir värdet av f(x)? Man säger att fuktionen är växande. Vilket är det minsta "godkända" värdet för f(x)?
I så fall
lika eller större än -1
Malisan74 skrev:Smaragdalena skrev:Malisan74 skrev:Smaragdalena skrev:Malisan74 skrev:Yngve skrev:Din graf stämmer inte riktigt. Funktionen är endast definierad för .
I det området (dvs på och till höger om y-axeln):
- Finns det något lägsta värde som y antar? I så fall vilket?
- Finns det något högsta värde som y antar? I så fall vilket?
- Finns det något värde mellan dessa som y inte antar? I så fall vilket/vilka?
Kan man på något sätt matematiskt räkna ut detta?
Inte omöjligt, men det enklaste och bästa sättet är att titta på bilden.
Borde vara -1 till 3?
Nej.
Titta på bilden. Eftersom definitionsmängden för f(x) är från och med 0 och uppåt, är det bara den del av kurvan som ligger på eller till höger om y-axeln som är intressanta. Ser du att ju mer du flyttar dig åt höger, desto större blir värdet av f(x)? Man säger att fuktionen är växande. Vilket är det minsta "godkända" värdet för f(x)?
I så fall
lika eller större än -1
Hur räknar du för att få f(0) till -1?
Smaragdalena skrev:Malisan74 skrev:Smaragdalena skrev:Malisan74 skrev:Smaragdalena skrev:Malisan74 skrev:Yngve skrev:Din graf stämmer inte riktigt. Funktionen är endast definierad för .
I det området (dvs på och till höger om y-axeln):
- Finns det något lägsta värde som y antar? I så fall vilket?
- Finns det något högsta värde som y antar? I så fall vilket?
- Finns det något värde mellan dessa som y inte antar? I så fall vilket/vilka?
Kan man på något sätt matematiskt räkna ut detta?
Inte omöjligt, men det enklaste och bästa sättet är att titta på bilden.
Borde vara -1 till 3?
Nej.
Titta på bilden. Eftersom definitionsmängden för f(x) är från och med 0 och uppåt, är det bara den del av kurvan som ligger på eller till höger om y-axeln som är intressanta. Ser du att ju mer du flyttar dig åt höger, desto större blir värdet av f(x)? Man säger att fuktionen är växande. Vilket är det minsta "godkända" värdet för f(x)?
I så fall
lika eller större än -1
Hur räknar du för att få f(0) till -1?
Räknade ej kollade på grafen Det är det jag vill friska upp minnet hur man räknar ut detta :)
Malisan74 skrev:Laguna skrev:Malisan74 skrev:När man ritar grafen är det dom skärpunkterna grafen får
Men hänger ej med riktigt på vad ni menar
Jag begriper fortfarande inte alls vad "x= 3,-1,-3 och y =-2" betyder. y är aldrig -2.
Nollställen men skrev fel på -2
Nollställena är två stycken. Varför står x=3 där?
Och hur bar du dig åt för att få f(0) till -1 när du tittade på grafen? Kan du rita dit en pil och lägga in bilden på nytt.
Jag tror det är bäst att förstå grafen helt och hållet innan man räknar ut något. Kan du markera i bilden var f antar sitt minsta värde?
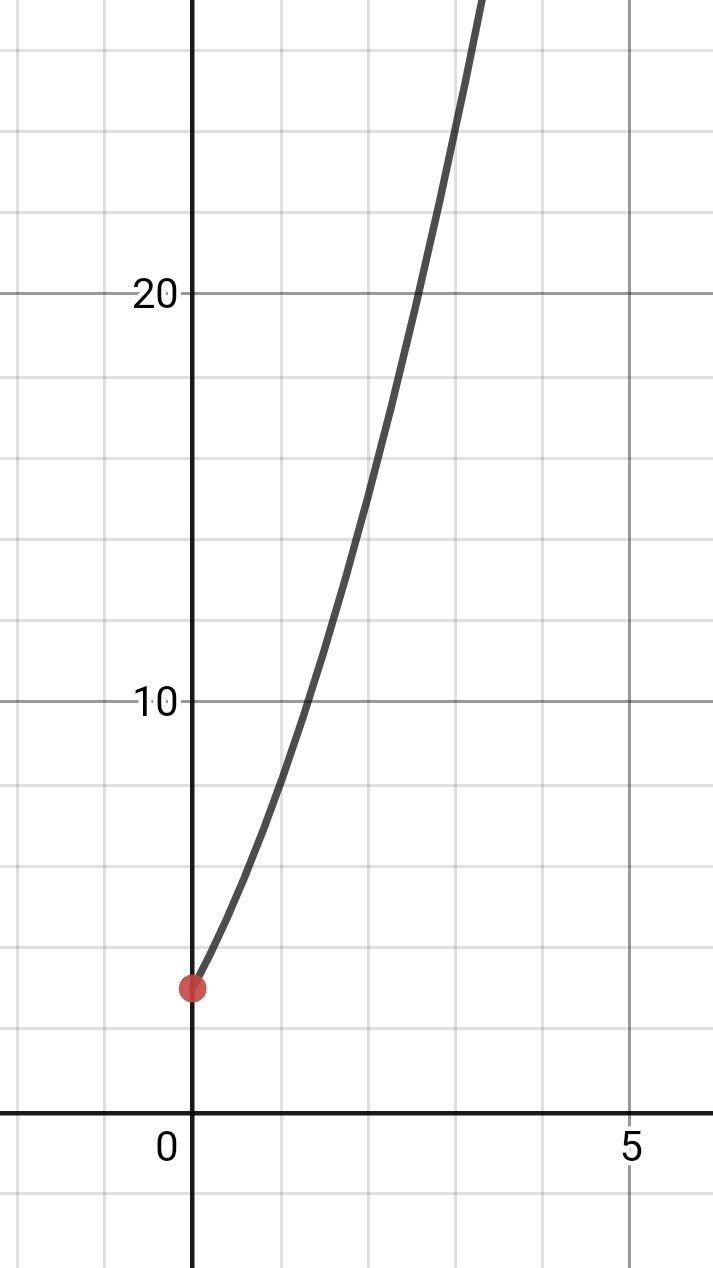
Jag tror att du inte riktigt har förstått vad det innebär att funktionens definitionsmängd är . Det innebär att den inte innehåller några värden på som är mindre än 0. Dessa värden är helt enkelt inte tillåtna.
Det innebär vidare att funktionens graf ser ut på följande sätt, dvs den sträcker sig inte till vänster om y-axeln.
Kan du då besvara frågan vilket funktionens minsta värde är?
Yngve skrev:Jag tror att du inte riktigt har förstått vad det innebär att funktionens definitionsmängd är . Det innebär att den inte innehåller några värden på som är mindre än 0. Dessa värden är helt enkelt inte tillåtna.
Det innebär vidare att funktionens graf ser ut på följande sätt, dvs den sträcker sig inte till vänster om y-axeln.
Kan du då besvara frågan vilket funktionens minsta värde är?
Definitionsmängen blir -3 och -1 på x axeln
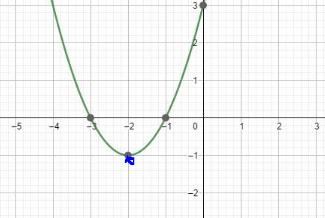 Minst f borde vara här
Minst f borde vara här
Malisan74 skrev:
Definitionsmängen blir -3 och -1 på x axeln
Du verkar ha missuppfattat vad en definitionsmängd är. Du kan repetera det begreppet genom att läsa detta avsnitt.
Läs först och fråga sedan här om det du inte förstår.
Yngve skrev:Malisan74 skrev:Definitionsmängen blir -3 och -1 på x axeln
Du verkar ha missuppfattat vad en definitionsmängd är. Du kan repetera det begreppet genom att läsa detta avsnitt.
Läs först och fråga sedan här om det du inte förstår.
Lugnt jag lägger ner att fråga här, här verkar man ej få någon förklaring och hjälp
Löser det själv
Malisan74 skrev:Yngve skrev:Malisan74 skrev:Definitionsmängen blir -3 och -1 på x axeln
Du verkar ha missuppfattat vad en definitionsmängd är. Du kan repetera
Lugnt jag lägger ner att fråga här, här verkar man ej få någon förklaring och hjälp
Löser det själv
Tråkigt att du känner så. Jag tycker att jag försökte att tydligt förklara vad funktionens definitionsmängd var och vad det innebar för grafen i detta svar.
- Läste du det svaret?
- Förstod du vad jag skrev?
Nu när jag tittar tillbaka i tråden så ser jag att vi har förklarat för dig 4 gånger att definitionsmängden inte innehåller negativa värden på x, men det verkar inte som om du har tagit det till dig.
Det är tråkigt att du ändå upplever det som att du inte har fått vare sig förklaring eller hjälp.
Hur tycker du att vi skulle ha gjort istället?
Yngve skrev:Malisan74 skrev:Yngve skrev:Malisan74 skrev:Definitionsmängen blir -3 och -1 på x axeln
Du verkar ha missuppfattat vad en definitionsmängd är. Du kan repetera
Lugnt jag lägger ner att fråga här, här verkar man ej få någon förklaring och hjälp
Löser det själv
Tråkigt att du känner så. Jag tycker att jag försökte att tydligt förklara vad funktionens definitionsmängd var och vad det innebar för grafen i detta svar.
- Läste du det svaret?
- Förstod du vad jag skrev?
Har nog missuppfattat allt, då jag bara snurrat runt med denna uppgift och inte fångat upp något, var längesen man gjorde detta
Läs igenom hela tråden igen, så blir det nog klarare!
ok jag börjar om från början här
minsta värde som f kan ta är väl 0?
Malisan74 skrev:ok jag börjar om från början här
minsta värde som f kan ta är väl 0?
Sätter jag noll i ekvationen får jag 3. svaret borde bli y>=3
Minsta vördet för x är 0. Det ger f(0)=3, som är det minsta värdet i värdemängden. Finns det något största värde?
Smaragdalena skrev:Minsta vördet för x är 0. Det ger f(0)=3, som är det minsta värdet i värdemängden. Finns det något största värde?
Borde inte finnas störst utan det är oändligt använder du dom tillåtna värden så ökar den bara hela tiden vilket även säger att den är injektiv finns inga x värden som har samma y värden