Värdemängd på en cylinder
En cylinder med radien x cm och höjden (x-3) cm. Vad är definitionsmängden och värdemängden.
Def är 0<x<3
Med värdemängden vet jag inte hur jag ska göra. Det måste lösas algebariskt eftersom vi inte får har grafritande verktyg.
Jag vet att volmen V(x) =
Jag vet inte hur jag ska göra sedan. Jag försökte med symmetri linje men de funkar ju enbart på andragradare...
Om uppgiften är formulerad precis som du skriver, får du tänka ett varv till på definitionsmängden samt funktionen för volymen.
r=x cm
h=x-3 cm
Du har skrivit att defintionsmängden är 0<x<3. Prova att sätta in x=1 och se vad som händer med höjden.
Du har ett annat uttryck för volymen. Där står det (3-x) för höjden.
Höjden är 3-x skrev fel i början
GoskJW skrev:Höjden är 3-x skrev fel i början
Finemang! Det verkar rimligt.
Har du koll på derivator? I så fall kan du hitta extrempunkterna för volymen lite lättare, utan digitala hjälpmedel.
Säg till om du behöver, så får du en puff i den riktningen.
Jag har koll på derivator och vet att man kan lösa det enkelt med derivata. Men just denna uppgift ska lösas utan derivata och blir därför svårare.
Kan du visa en bild på uppgiften?
GoskJW skrev:Jag har koll på derivator och vet att man kan lösa det enkelt med derivata. Men just denna uppgift ska lösas utan derivata och blir därför svårare.
Ja, då blir det lite kärvare. Står det alltså i uppgiften att du inte får derivera? Märkligt i så fall! Det här är ju ett bra exempel på när det är riktigt användbart.
Laguna skrev:Kan du visa en bild på uppgiften?
Vi får väl anta att frågan gäller definitions- och värdemängd av V(x).
Radien (d.v.s. x) borde kunna anta alla värden större än 0. Men vad blir värdemängden? Ja, sätt in "giltiga" x i V(x) och se vad det blir.
sictransit skrev:GoskJW skrev:Jag har koll på derivator och vet att man kan lösa det enkelt med derivata. Men just denna uppgift ska lösas utan derivata och blir därför svårare.
Ja, då blir det lite kärvare. Står det alltså i uppgiften att du inte får derivera? Märkligt i så fall! Det här är ju ett bra exempel på när det är riktigt användbart.
Nej men detta är kapitlet innan derivata och vi har prov på detta och från inte använda derivata.
Laguna skrev:Kan du visa en bild på uppgiften?
Vi får använda räknare men inte graftritande
GoskJW skrev:Laguna skrev:Kan du visa en bild på uppgiften?
OK. Men jag ser ingenstans att du inte får derivera. Eller? Alltså ta fram ett uttryck för V’(x).
sictransit skrev:GoskJW skrev:Laguna skrev:Kan du visa en bild på uppgiften?
OK. Men jag ser ingenstans att du inte får derivera. Eller? Alltså ta fram ett uttryck för V’(x).
1.3 verkar tidigt för derivata. Jag gissar att rutat uppg.nr. betyder = grafritare och deras "Max-funktion" skall användas.
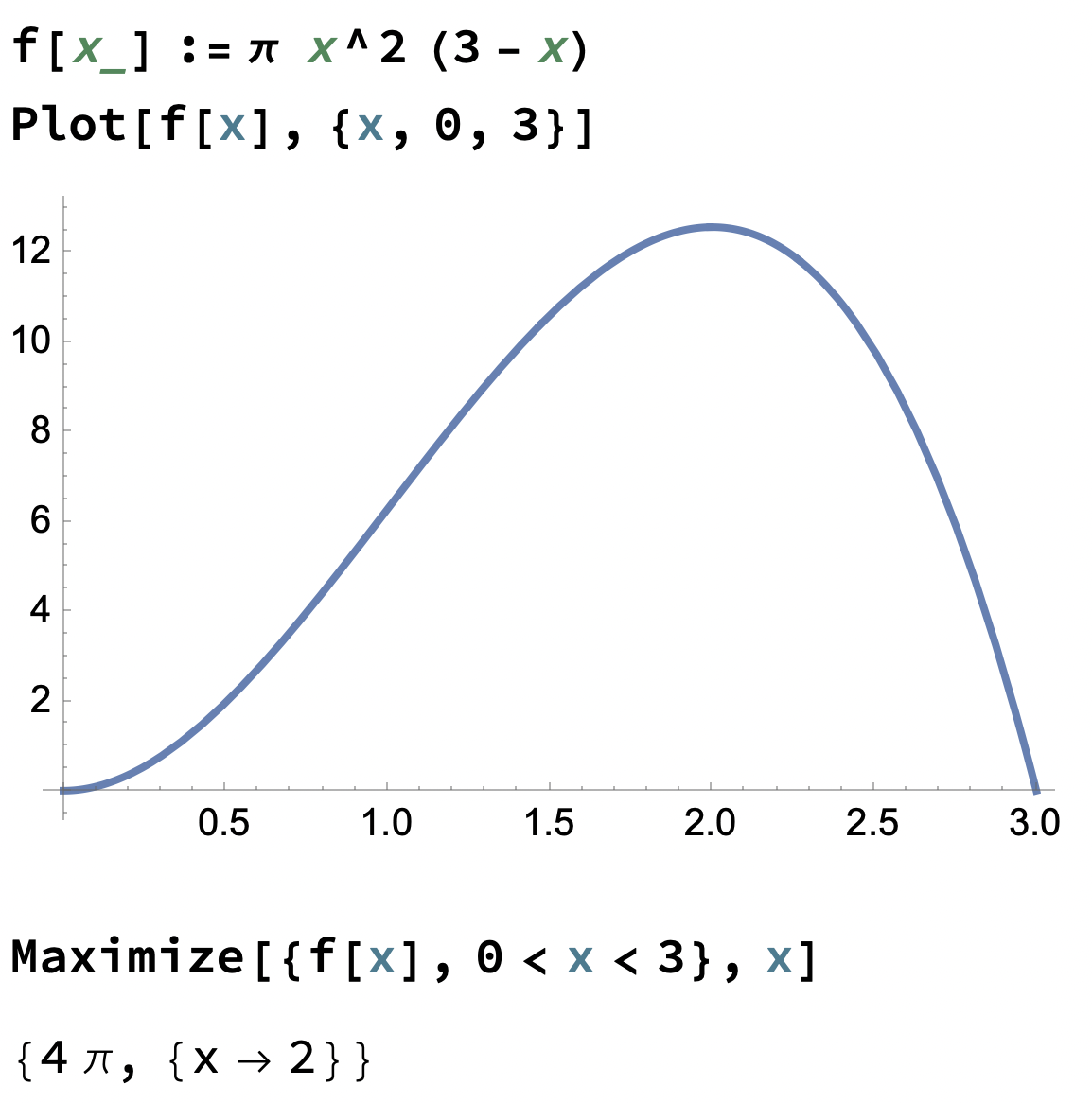
TS skrev att ruta betyder:
Vi får använda räknare men inte graftritande
sictransit skrev:TS skrev att ruta betyder:
Vi får använda räknare men inte graftritande
Aha, my bad
kanske hederlig funktionstabell?
måste ha föregåtts av exempel i boken som visar på föreslagen metod
sictransit skrev:TS skrev att ruta betyder:
Vi får använda räknare men inte graftritande
Problemet är att rutan inte betyder detta. Denna övningsuppgift skall lösas m.h.a. ett digitalt verktyg. Man sätter dock ingen begränsning på vilken sorts digitala verktyg det handlar om.
Uppgift 1328 säger inte att man ska lösa den algebraiskt, så grafritande räknare går alldeles utmärkt att använda.
Det är mycket väl möjligt att man inte får använda grafritande miniräknare på provet, men så är inte fallet i denna övning från boken. Vill man klara sig i denna övning utan derivatan och utan grafritande/symbolhanterande räknare, så går det att hitta en lösningsmetod för tredjegradsuttryck. Den metoden kommer dock upplevas som mörk magi för en elev som läser Ma3c. (Är du intresserad, så kan jag skriva ett inlägg med en lösning utan derivatan och utan digital verktyg, men jag är tveksam att det kommer att ha någon nytta...)
Bra där! Då blev förutsättningarna rimliga helt plötsligt.
Jag valde också att inte blanda in den ”svarta magin”, lösa tredjegradare för hand.
Nu återstår att peta in uttryck och definitionsmängd som TS redan funnit i valfritt verktyg.
(Om sedan derivata kommer i nästa kapitel, som TS skriver, blir det ju en fin pedagogisk poäng hur lätt det blir sedan.)
