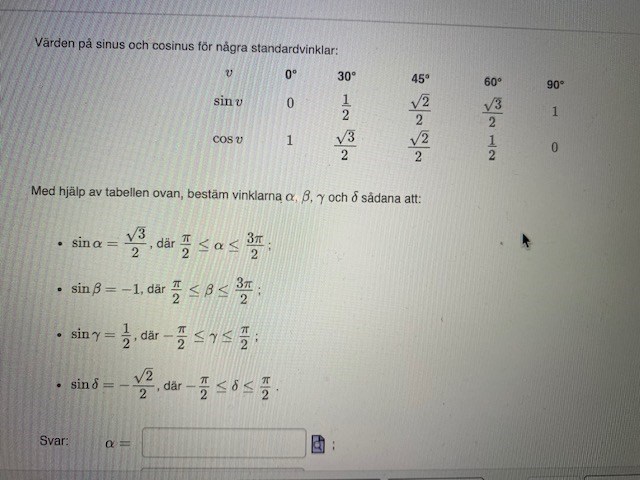
Värden på sinus och cosinus för några standardvinklar:

Rita "enhetscirkeln"

Kommer du vidare?

"Standardvinklarna" bestäms enklast från proportionerna hos en halv kvadrat och en liksidig triangel delad i två.

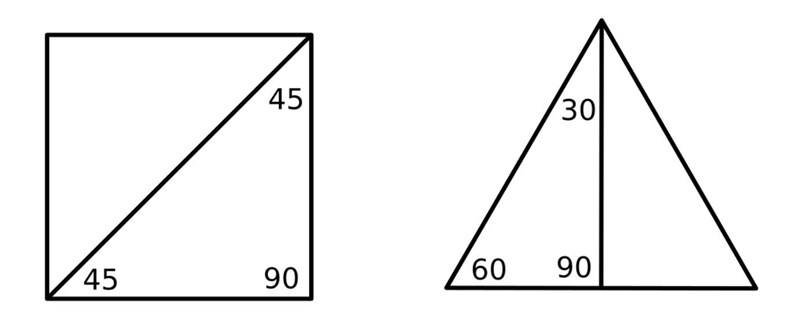
Bara sätt kvadratens och triangelns sida till 1 och bestäm kvoterna. 

För uppgiften behöver man dock inte kunna härleda dem.

Man kan även härleda dem från komplexa tal men detta är standardviset jag förväntar mig att alla borde kunna förr eller senare. 

okej men det enda jag ska göra då är att ta reda vilken vinkel som dem har:

har jag fattat rätt om jag gör såhär:

$$\begin{gathered} \sin \alpha =60° \\ \sin \beta =-90° (osäker= \\ \sin \gamma =30° \\ \sin \delta =-45° \end{gathered}$$

jag har läst av tabellen.

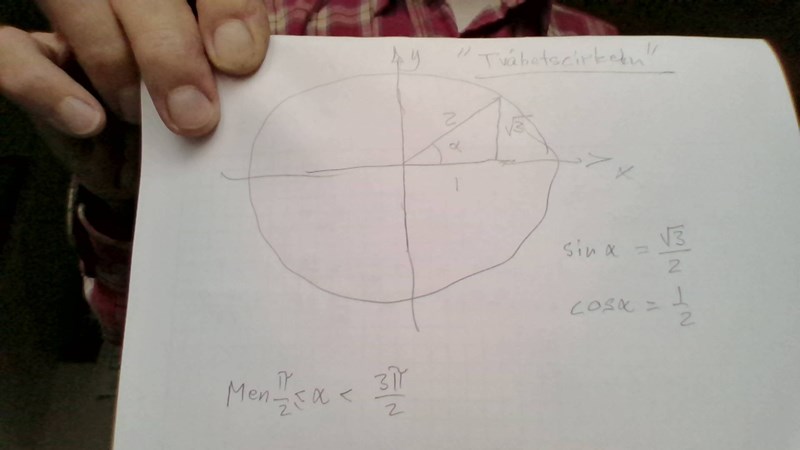
I vilken kvadrant ligger då alfa?

i första??

$\sin \alpha =\frac{\sqrt{3}}{2}=60° där \frac{\mathrm{\pi }}{2}=90° och \frac{3\mathrm{\pi }}{2}=270°$???

jag fattar inte hur jag ska göra det här

ska jag omvandla gradet till radianer?? TEX: för att få radian gör man x(pi/180) vilket ger $60°\left(\frac{\mathrm{\pi }}{180}\right) = \frac{60}{180}*\mathrm{\pi }= \frac{6}{18}\mathrm{\pi }$

är det rätt??

$\sin 60°=\frac{\sqrt{3}}{2} är korrekt men denna vinkel ligger i första kvadranten dvs 0\le \alpha \le \frac{\pi }{2}$

$Vilken vinkel har samma \sin usvärde som 60° men ligger i 2:a till 3:e kvadranten dvs \frac{\pi }{2}\le \alpha \le \frac{3\pi }{2}$

-$\frac{\mathrm{\pi }}{6}$?

jag förstår ingenting av det här.

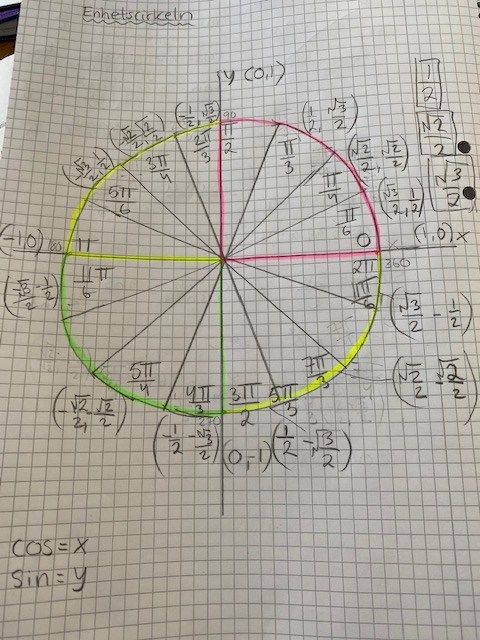
Sinusvärdet avläses på y-axeln

Cosinusvärdet avläses på x-axeln

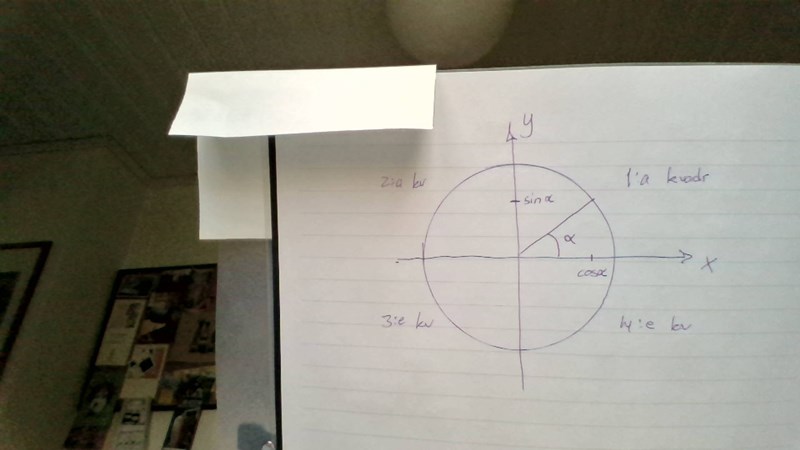
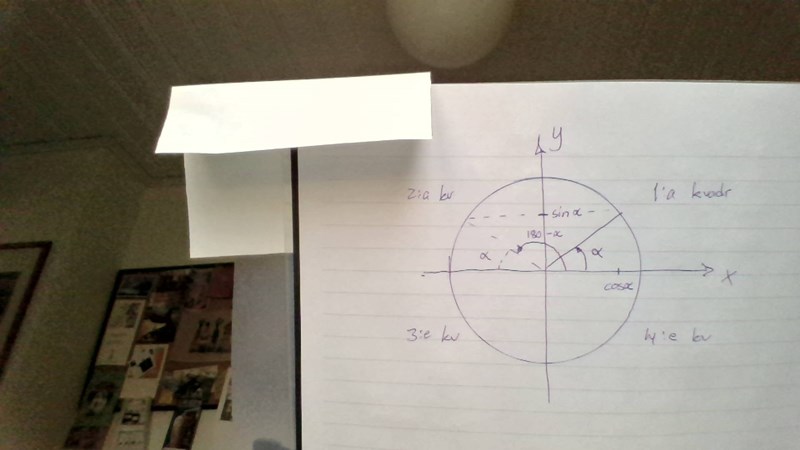
Vilken vinkel har samma sinusvärde som 60° men ligger i 2:a till 3:e kvadranten dvs π/2≤α≤3π/2

-1/2?

$\sin \left(\alpha \right)=\sin (180°-\alpha )$

Läs gärna lite  https://www.matteboken.se/lektioner/matte-3/trigonometri/enhetscirkeln

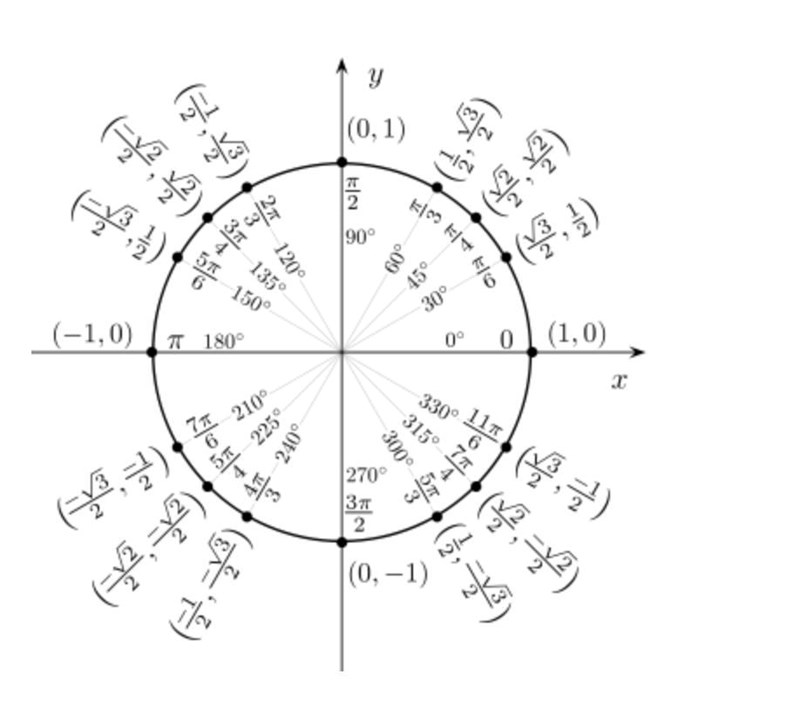
Om jag har den här så ska jag alltså bara lösa av där sin$\alpha$=$\frac{\sqrt{3}}{2}$

då stämmer det att det ska vara $\frac{\mathrm{\pi }}{3}$?

Det finns två punkter på enhetscirkeln som har y-koordinaten $\frac{\sqrt{3}}{2}$. Jag har markerat dem i bilden.

Det betyder att det i intervallet $0\leq v<2\pi$ finns två vinklar, vars sinusvärde är $\frac{\sqrt{3}}{2}$.

Du ska välja den vinkel som passar in i det givna intervallet.

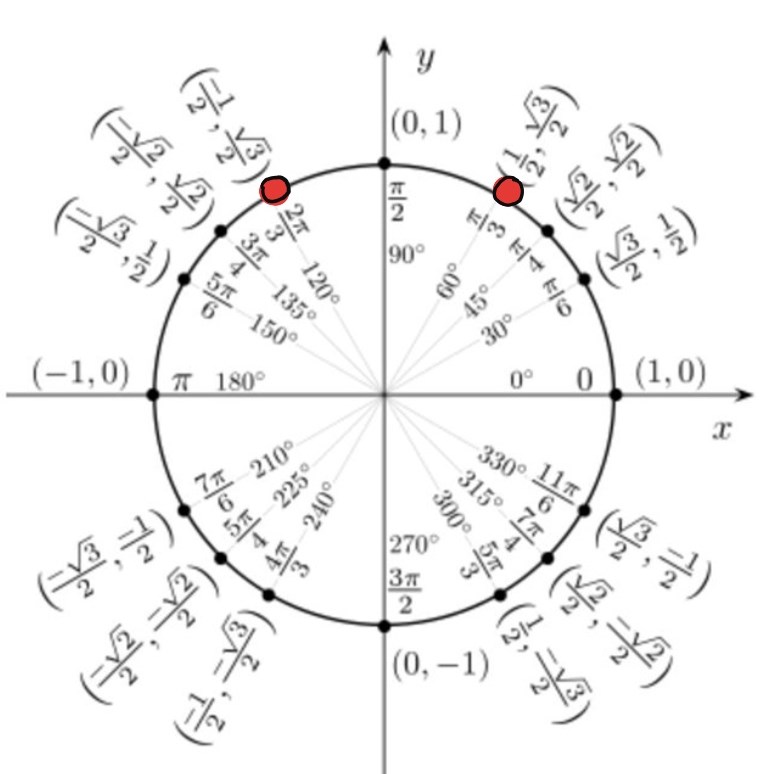
i detta fall måste det vara $2\mathrm{\pi }/3$eftersom det skulle ligga mellan andra och tredje kvadranten?

Den första var isf relativt enkel men hur ska jag tänka med dem andra? känns som det blir svårt på dem andra. Vart är sin -1? och intervallet som är $-\frac{\mathrm{\pi }}{2}\le \gamma \le \frac{\mathrm{\pi }}{2}$

Nej, nästa uppgift är inte svår om man har lärt sig förstå enhetscirkeln. Det du vill ta fram är storleken på den vinkel som gör att sinus för vinkeln är -1, d v s att y-värdet är -1. Vinkeln räknas alltid från den positiva x-axeln.

Ser du att den punkt där enhetscirkeln har y-värdet -1 är längst ner? Den här uppgiften är lättare än a-uppgiften, eftersm det bara finns en punkt vi behöver bry oss om.

Joh_Sara skrev:

i detta fall måste det vara $2\mathrm{\pi }/3$eftersom det skulle ligga mellan andra och tredje kvadranten?

Det stämmer. Men inte "mellan" utan i andra eller tredje kvadranten, dvs i vänstra halvplanet.

åh nu ser jag. detta börjar ju släppa nu. :) 

så då är följande:

$$\begin{gathered} \sin \alpha \frac{\sqrt{3}}{2} i andra eller tredje kvadranten = \frac{2\mathrm{\pi }}{3} \\ \sin \beta -1 i andra eller tredje kvadranten = \frac{3\mathrm{\pi }}{2} \\ \sin \gamma \frac{1}{2} i -\frac{\mathrm{\pi }}{2}\le \gamma \le \frac{\mathrm{\pi }}{2} är jag osäker. Antingen är det \frac{\mathrm{\pi }}{6}eller\frac{5\mathrm{\pi }}{6} \\ \sin \delta -\frac{\sqrt{2}}{2}-\frac{\mathrm{\pi }}{2}\le \gamma \le \frac{\mathrm{\pi }}{2}är jag osäker. Antingen är det \frac{5\mathrm{\pi }}{4} eller \frac{7\mathrm{\pi }}{4} \end{gathered}$$

De första två är rätt.

Men du ska skriva så här:

Om $\sin(\alpha)=\frac{\sqrt{3}}{2}$ och vinkeln $\alpha$ ligger i andra eller tredje kvadranten så är $\alpha=\frac{2\pi}{3}$.

==========

För de sista två frågorna gäller följande:

$-\frac{\pi}{2}\leq\gamma\leq\frac{\pi}{2}$ innebär att punkten ligger i fjärde eller första kvadranten.

Sanma sak gäller för vinkeln $\delta$.

Hej,

Vinkeln $\alpha$: Du vet att den ligger mellan 90 grader och 270 grader. Dess sinusvärde är $\sqrt{3}/2$ så enligt tabellen kan $\alpha$ vara 60 grader, men den vinkeln ligger ju inte mellan 90 och 270 grader.  Men sinusfunktionen är sådan att vinkeln $180 - \alpha$ har samma sinusvärde som $\alpha$, och den vinkeln är 120 grader och ligger i det tillåtna intervallet. Den sökta vinkeln är alltså 120 grader.

Vinkeln $\beta$: Du vet att den ligger mellan 90 grader och 270 grader. Dess sinusvärde är $-1$ men tabellen kan inte hjälpa till här. Istället ska man veta att vinkeln 270 grader har sinusvärdet $-1$, varför den sökta vinkeln är 270 grader. 

Vinkeln $\gamma$: Du vet att den ligger mellan $-90$ grader (räknas alltså medurs) och 90 grader. Dess sinusvärde är $1/2$ så enligt tabellen kan $\gamma$ vara 30 grader, vilket ligger i det tillåtna intervallet. Den sökta vinkeln är 30 grader.

okej så då blir

 $$\begin{gathered} \sin \left(\gamma \right)=\frac{1}{2} i första eller fjärde kvadranten så är \gamma =\frac{\mathrm{\pi }}{6} \\ \sin \left(\delta \right)=-\frac{\sqrt{2}}{2} i första eller fjärde kvadranten så är \delta =\frac{7\mathrm{\pi }}{4} \\ Stämmer detta? \end{gathered}$$

Det första är rätt men inte det andra.

Vinkeln $\frac{7\pi}{4}$ ligger inte i intervallet $[-\frac{\pi}{2},\frac{\pi}{2}]$.

Du kan tänka så här:

Eftersom sinusfunktionen är periodisk med perioden $2\pi$ så gäller att $\sin(v)=\sin(v-2\pi)$.

Alltså gäller att $\sin(\frac{7\pi}{4})=\sin(\frac{7\pi}{4}-2\pi)=\sin(-\frac{\pi}{4})$.

hmm förstår nog inte riktigt. Hur kan det bli -pi/4?

Ur enhetscirkeln ser du att två lösningar till ekvationen $\sin(\delta)=-\frac{\sqrt{2}}{2}$ är $\delta=\frac{5\pi}{4}$ och $\delta=\frac{7\pi}{4}$.

Eftersom sinusfunktionen är periodisk med perioden $2\pi$ så kan alla ekvationens lösningar skrivas $\delta=\frac{5\pi}{4}+n\cdot 2\pi$ och $\delta=\frac{7\pi}{4}+n\cdot2\pi$.

Om du väljer $n=-1$ ur den sistnämnda lösningsmängden så får du den lösning som ligger i det önskade intervallet.

Jämför din tidigare fråga angående val av konstanten $n$ för att hitta lösningar i ett visst intervall.

okej nu är jag med. Tack för all hjälp.