Varför fungerar inte min metod?

Om x² + y² = 49, så kan y bara ligga mellan -7 och 7. Så du får minsta värde då y = -7.

Jag förstår inte riktigt vad du menar.

Du har visat att x² + y² = 49.

Om |y| > 7 så skulle det då betyda att x² < 0. Vilket inte är möjligt då kvadraten på ett reellt tal alltid är större än eller lika med 0.

Således måste |y| $\le$ 7 .

Jag är inte någon höjdare på komplexa tal och vet inte hur man löser algebraiskt, men ser det så här framför mig:

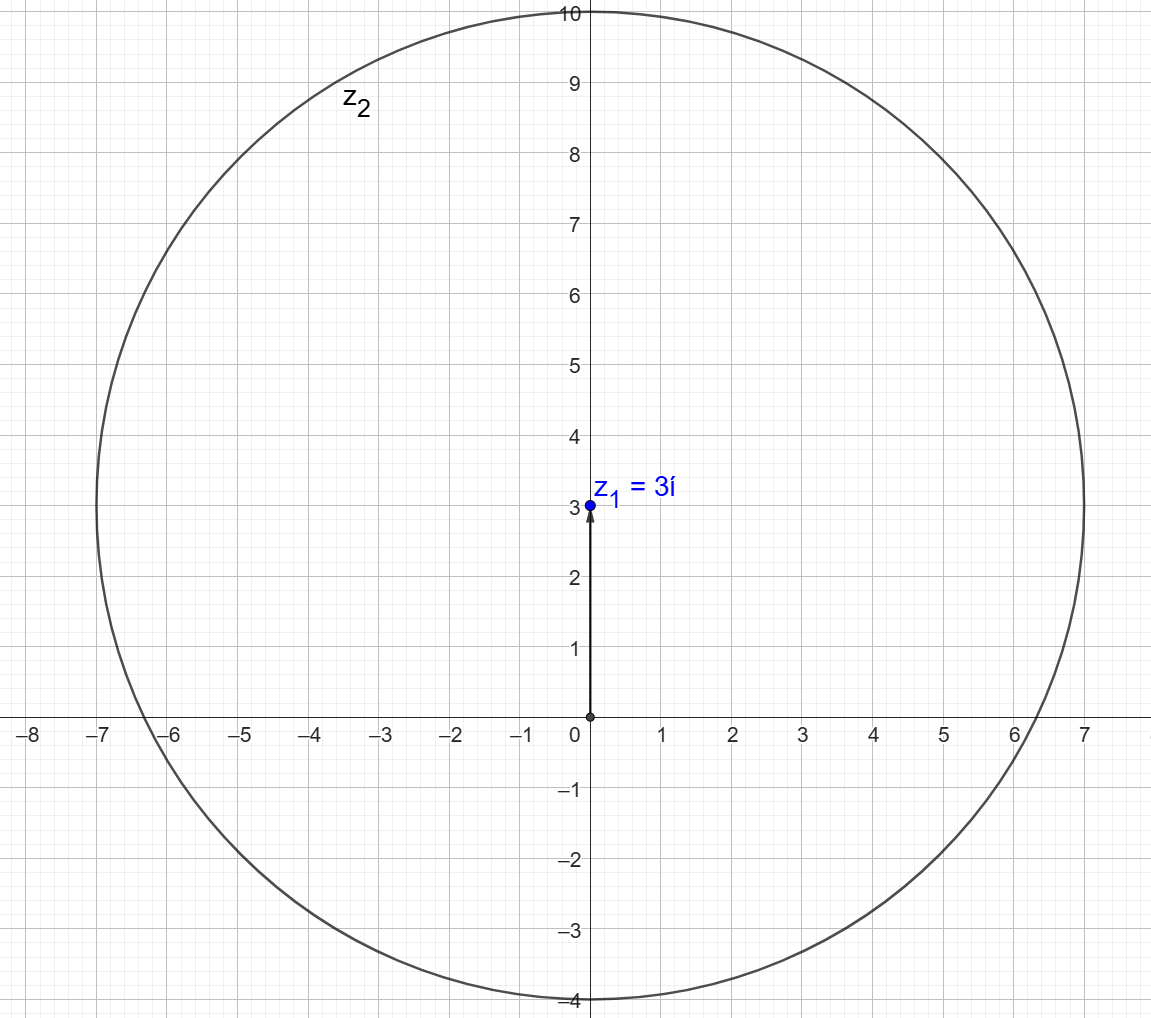
z₁=3i och |z₂|=7. Då kommer z1+z2 att hamna någonstans på cirkeln. För att |z1+z2| skall vara så litet som möjligt så måste z₂ peka i motsatt riktning mot z₁.

Hur vet du att talet måste hamna på en cirkel med radien 7? Det var väl Z2 som hade längden 7? Kommer då också Z1 + Z2 ha samma längd?

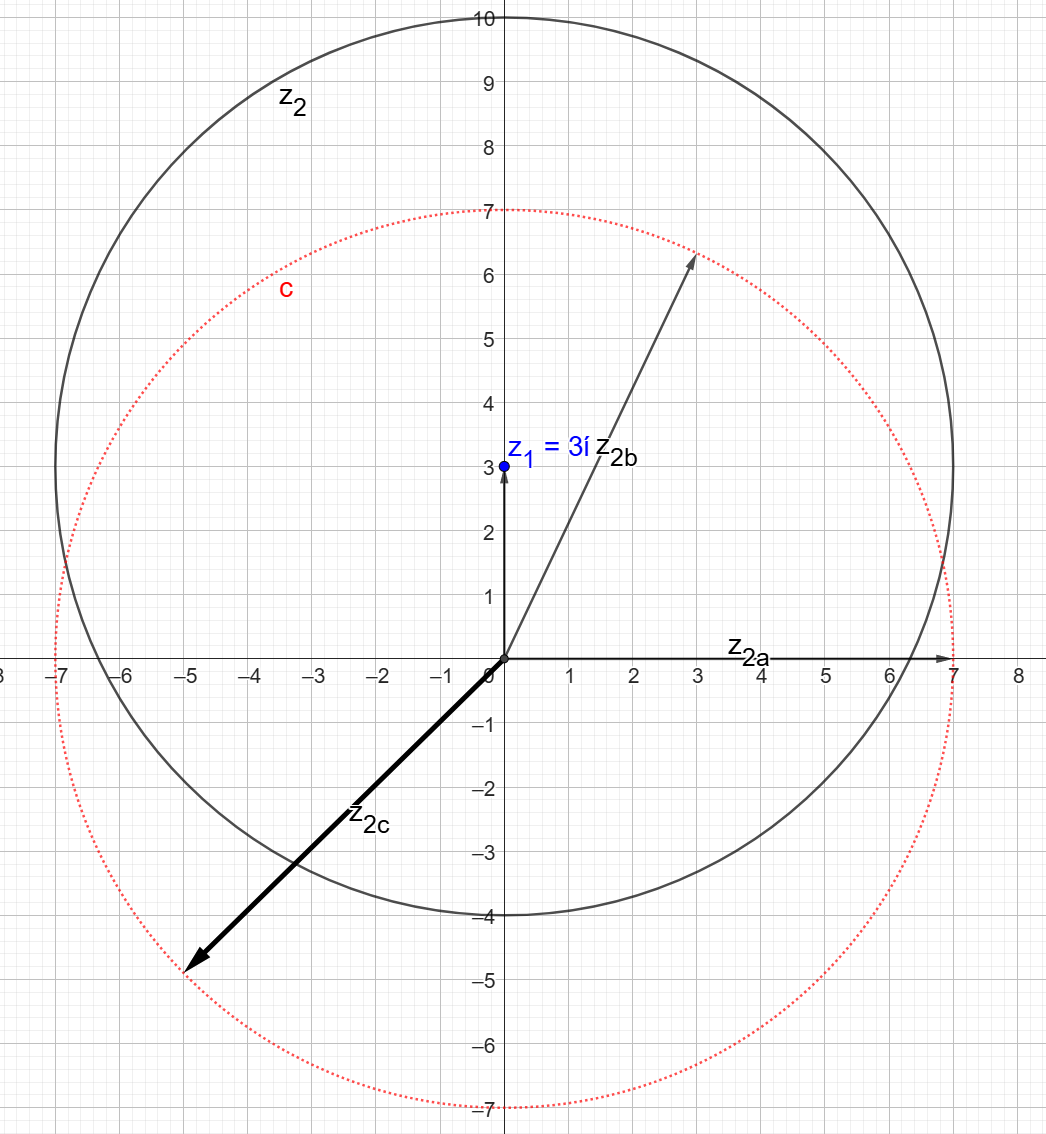
Här är tre varianter på z₂:

• z_2a=7
• z_2b=3+2i√10
• z_2c=-5-2i√6

Gemensamt är att |z₂|=7, alltså radien på den röda cirkeln som utgår ifrån origo.

Om du tar z₁+z₂, så lägger du vektorn z₂ efter z₁ och hamnar på den svarta cirkeln.

|z₁+z₂| är då avståndet från origo till den nya ändpunkten. 

Tror jag förstår lite bättre nu! Men det går alltså inte att bevisa algebraiskt som jag försökte med genom att ansätta Z2 till x+ yi?

Anonym_15 skrev:

Tror jag förstår lite bättre nu! Men det går alltså inte att bevisa algebraiskt som jag försökte med genom att ansätta Z2 till x+ yi?

Det går säkert, men jag kan inte.

Jag delade bara med mig av ett annat sätt att se på problemet. Då ser jag att vid z₂=-7i blir beloppet minimalt, alltså =4. 

Anonym_15 skrev:

Tror jag förstår lite bättre nu! Men det går alltså inte att bevisa algebraiskt som jag försökte med genom att ansätta Z2 till x+ yi?

Jo, det går. Men i din lösning måste du ta hänsyn till att |y|$\le$7.

Tack ändå! Är det någon annan som vet hur man kan lösa uppgiften algebraiskt?

Fördelen med att hänga här är att man får repetera sådant man eventuellt lärde sig för decennier sedan, eller kanske aldrig riktigt fattade där och då.

Jag gör ett försök, fast i polär form.

Ett komplext tal z med absolutbeloppet (radien) r kan skrivas som: $z=r\left(\cos \phi +i\sin \phi \right)$

Eftersom |z₂|=7 kan vi skriva: $z_2=7\left(\cos \phi +i\sin \phi \right)$. 

Då har vi: $z_1+z_2=3i+7\left(\cos \phi +i\sin \phi \right)=7\cos \phi +i(7\sin \phi +3)$

Absolutbeloppet: 

$$\begin{gathered} \left|z_1+z_2\right|=\sqrt{{\left(7\cos \phi \right)}^2+{(7\sin \phi +3)}^2} \\ =\sqrt{49{\cos }^2 \phi +{(7\sin \phi +3)}^2} \\ =\sqrt{49{\cos }^2 \phi +49{\sin }^2 \phi +9+42\sin \phi } \\ =\sqrt{49({\cos }^2 \phi +{\sin }^2 \phi )+9+42\sin \phi } [\mathrm{trig} 1:\mathrm{an}] \\ =\sqrt{49+9+42\sin \mathrm{\phi }} \\ =\sqrt{58+42\sin \mathrm{\phi }} \end{gathered}$$

$\sin \phi$ får sitt minsta värde (=-1) då $\phi =\frac{3\mathrm{\pi }}{2}=270°$, alltså rakt nedåt. Nu börjar det verka lovande, eller hur?

$\sqrt{58+42\sin \frac{3\mathrm{\pi }}{2}}=\sqrt{58+42\times -1}=\sqrt{58-42}=\sqrt{16}=\boxed{4}$

Där har vi det minsta värdet av $\left|z_1+z_2\right|$.

Tyvärr är detta fortfarande inte ett svar på din ursprungliga fråga, men jag lyckades pilla ut lösningen utan grafiska hjälpmedel i alla fall.

Det känns lite som om jag visat att om man går 3 steg åt ett håll och sedan måste gå 7 steg till, så kommer man närmast den ursprungliga positionen om man går tillbaka samma väg som man kom. :-)

Vi kan ju prova att sätta $\phi =\mathrm{\pi }$ och alltså addera z₂=-7 till z₁:

$=\sqrt{58+42\sin \mathrm{\pi }}=\sqrt{58}\approx 7,62$

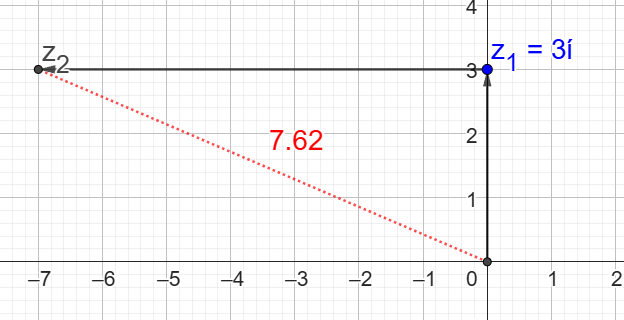
Funkar! Jag har lärt mig något idag. Tack för frågan!

PS. Din ursprungliga uppställning har ju många likheter med min, så det måste vara rätt spår någonstans. 58:an dyker upp, om inte annat.

Tack! Nu klarnade det till! Så konstigt bara att metoden ej fungerar om man skriver på rektangulär form. Det gör det svårt för mig att veta om jag kan använda min egen metod eller ej om en liknande uppgift dyker upp.

Anonym_15 skrev:

Tack! Nu klarnade det till! Så konstigt bara att metoden ej fungerar om man skriver på rektangulär form. Det gör det svårt för mig att veta om jag kan använda min egen metod eller ej om en liknande uppgift dyker upp.

Bra att det klarnade! Kanske hoppar någon in här som är bättre på detta än jag och ger en briljant lösning på problemet. Vi får se.

Jag ser att du är nöjd men något bra svar på varför din lösning inte funkar har du nog inte fått. Jag har tyvärr inget "briljant" att komma med men lite mer ledtrådar kanske?

Du vill minimera |z₁+z₂| med bivillkoret |z₂|=7. När du sätter "diskriminanten till 0" så inför du ett motstridigt villkor. Då säger du att |z₁+z₂|=0 och det finns bara 1 lösning på det,  z₂=-z₁, men det uppfyller ju inte bivillkoret. (Detta trots att du använder bivillkoret för att hitta diskriminanten, och det är här som även mina kunskaper blir lite svajiga...)

Det är ungefär det som patenteramera skriver i inlägg 2 och 4 ovan.