Varför funkar inte denna lösning?

Eftersom koefficienterna i polynomet är heltal och det är en skoluppgift, så finns det hopp att en av lösningarna är ett heltal. Heltalslösningen måste då vara en av delare till konstanta koefficienten, d.v.s. till -6:an. Pröva sätta in x=±1, ±2, ±3, ±6.

När du hittat en lösning, så kan du utnyttja faktorsatsen och minska gradtalet m.h.a. polynomdivisionen (liggande stolen)

tveksamt om polynomdivision är känt i Matte 3

Om inte:

Hitta en lösning enligt #1, anta att lösningen är x = a

Då ska 

(x-a)(x^2+bx+c) = x^3-x^2+x-6

Sätt in ditt värde på a, multiplicera ihop VL och bestäm konstanterna b och c.

Sen är det bara att lösa andragradsekvationen (x^2+bx+c=0)

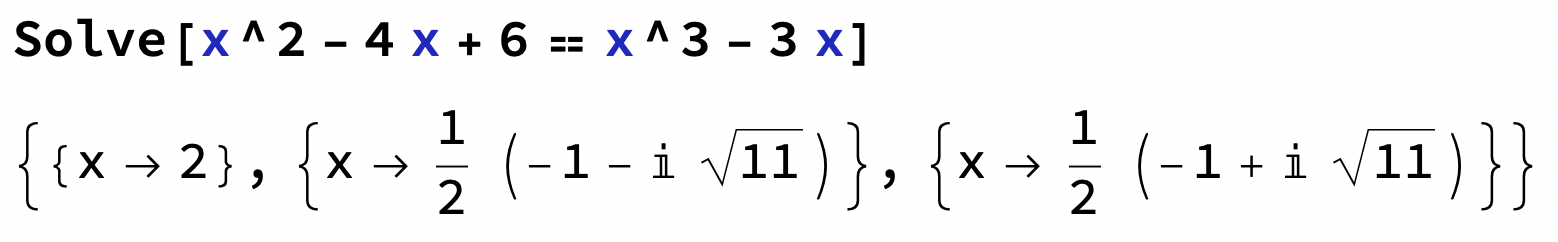
Komplexa tal i Ma3?

Tures metod funkar, men det verkar bara finnas en reell rot. VL i den andragradsekvationen man får kan kvadratkompletteras för att visa att VL>0 för alla x. Komplexa rötter har vi inte i Ma 3 vad jag vet.

Efter en titt i "Matteboken 3" verkar det som om:

- Man skall prova faktorer i 6, d v s 1, 2, 3 och finna att x=2 är en rot

- Sen kan man multiplicera ihop (x-2)(x² +ax +b) och identifiera koefficienter för att 

 finna att a=1 och b=3

- I matteboken nämns faktiskt att det finns andragradsekvationer som inte har reella

lösningar (roten i p-q-formeln är negativ)

Okej så kan någon förklara steg för steg hur jag löser: 

f(x) = x^3 - 5x^2 + 9

Charlieb skrev:

Okej så kan någon förklara steg för steg hur jag löser: 

f(x) = x^3 - 5x^2 + 9

Menar du f(x)=0?

Den har inga 'enkla' lösningar

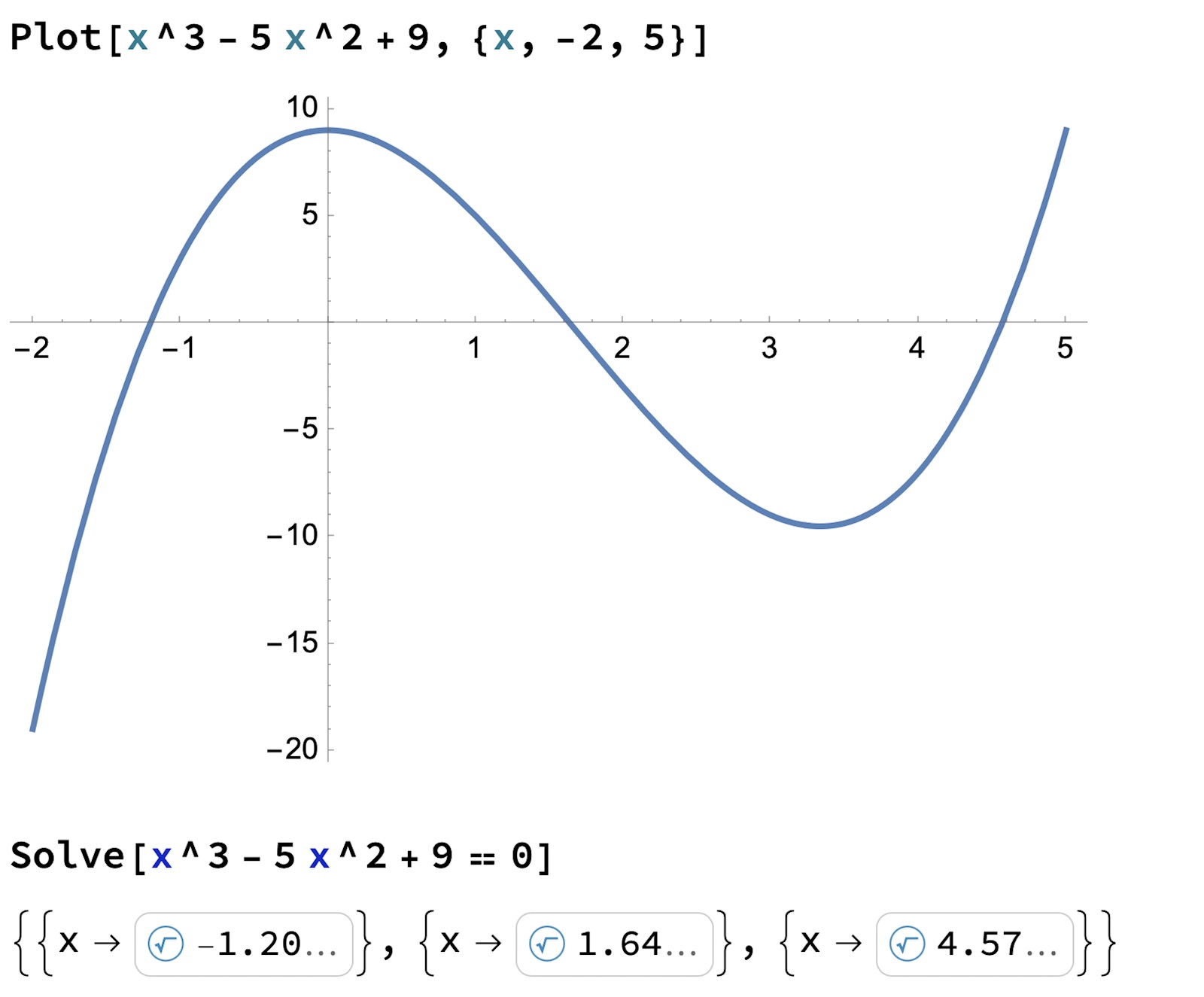
Polynomdivision kommer, som nämnts ovan, först i Ma4.

Okej, så för att lösa 0 = x^3 - 5x^2 + 9

Hur gör man det algebraiskt? Trots att den inte har några "enkla" lösningar

För ekvationer av tredje och fjärde graden finns motsvarigheter till "pq-formeln". Den ende jag sett använda dem är salig prof. Hanner. De fyllde en hel skrivtavla men fyller ingen med lust lära. För ekv. av högre grad än så har man däremot m h a Galoisteori bevisat att det inte finns några sådana metoder. Det är pedagogisk katastrof att ge en tredjegradsekv av denna typ på ma 3 utan att ge någon hint t ex att tillåta grafisk lösning.

Charlieb skrev:

Okej, så för att lösa 0 = x^3 - 5x^2 + 9

Hur gör man det algebraiskt? Trots att den inte har några "enkla" lösningar

Det blir väldigt svårt. När du har tredjegradare så gäller det att faktorisera mha av polynomets nollställen. Dessa brukar vara heltal, för att göra uppgiften rimlig. Detta är också ma4. 

I just det polynomet du gav så finns det inga heltalslösningar, vilket gör uppgiften i princip omöjlig att lösa på "rimliga" sätt. Det du KAN göra är att lösa det numeriskt =) T.ex https://sv.wikipedia.org/wiki/Newtons_metod

Det är inget supersvårt, utan det är en iterativ process för att hitta nollställen. Detta ingår dock inte i gymnasiemattematiken, så vitt jag vet.

Okej, då förstår jag. Tack så mycket!!