Varför gör man spänningsdelning?
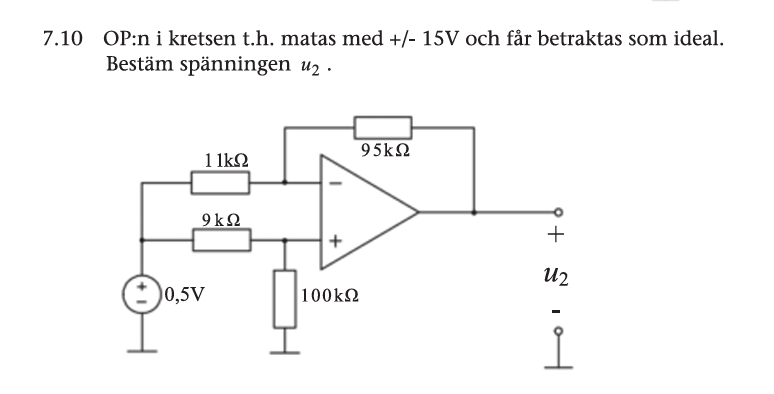
I följande uppgift förstår jag inte varför man gör en spänningsdelning just över motståndet som är 100 kΩ. Beräkningen sker genom att använda (100 / (9 + 100)) × 0,5. Min fråga är varför man utgår från just 100 kΩ? Är det för att resistorn är nära spänningarna V- och V+? Jag förstår inte logiken bakom detta och hade uppskattat om någon kunde förklara varför man gör på just det här sättet. Tex löser min lärare genom det sättet 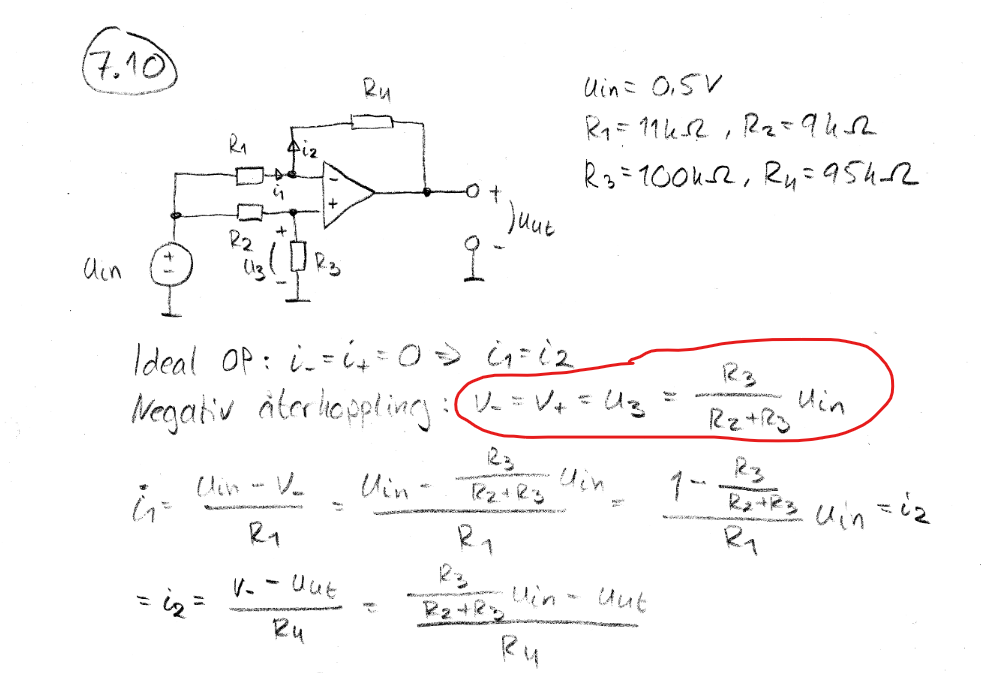
Kunde man inte lika gärna gjort (R2 / R3 + R2)*0,5 ? dvs (9 / (10 + 9)) * 0,5 ?
Spänningen på +ingången, alltså U3 blir Uin*R3/(R2+R3) = 0.5*100(9+100) = 0.459V. Den är helt oberoende av vad OP:n gör.
Utgången på OP:n kommer sen att se till att spänningen på -ingången blir samma.
Jag tycker det ser ut som uträkningen inte är färdig. Det frågades ju om Uut.
Ja, uträkningen är inte helt färdig, men jag har löst uppgiften. Det enda jag var förvirrad över var själva spänningsdelningen.
Jag håller med om att det är en lite knepig koppling.
Om R3 = R4 och R1 = R2 så hade man haft en ren skillnadsförstärkare.
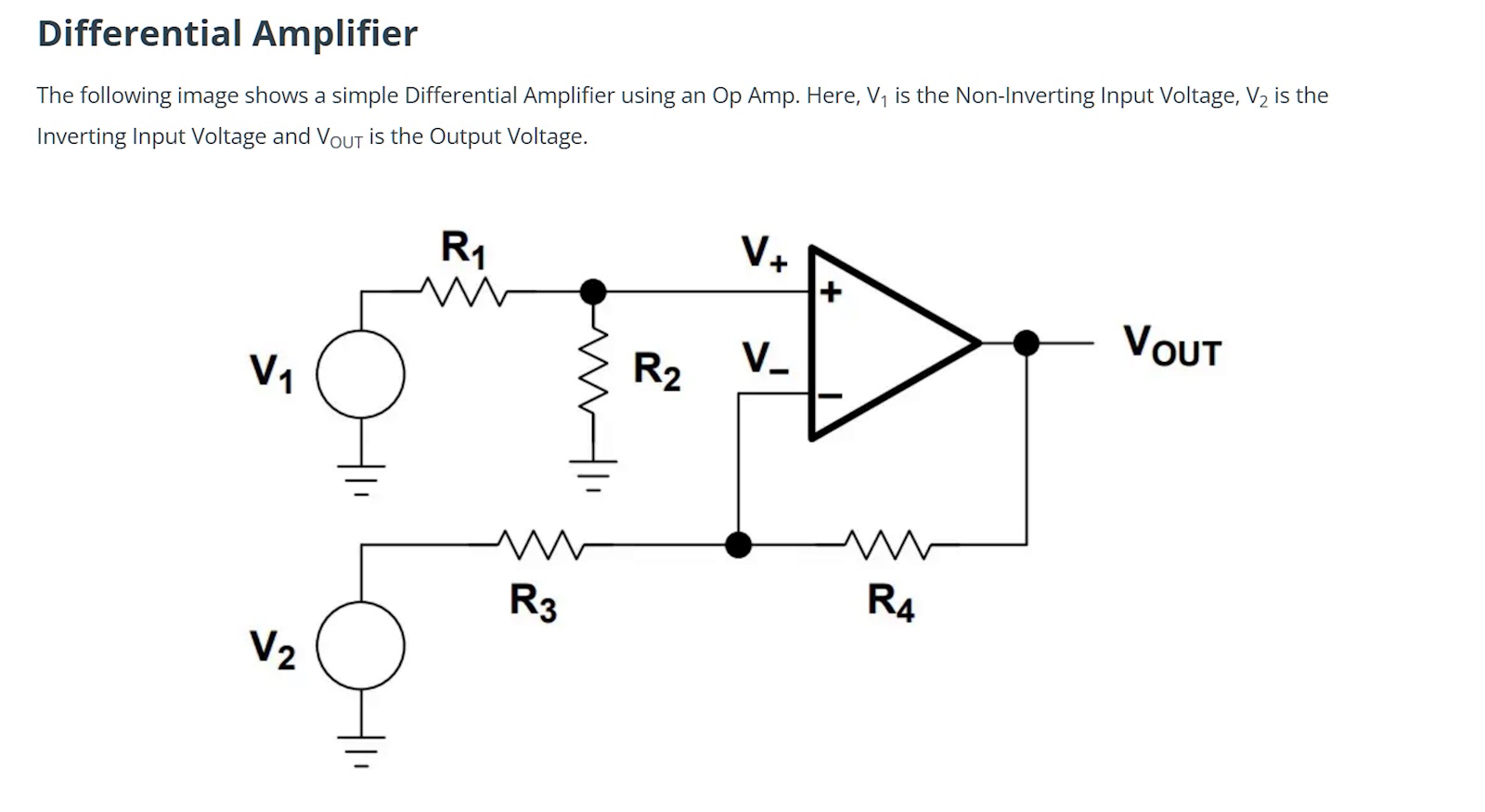
Men så är det inte i uppgiften.
Att beräkna spänningsdelning enligt ditt förslag i inlägg #2 hade varit lämpligt om strömmarna genom R1 och R2 vore lika. Nu är det ingångsspänningarna till OP’n som är lika, och dessa bestäms av spänningen över R3.




