Varför kan Moa inte använda sig av induktionsbevis?
Hej jag behöver hjälp med a) uppgiften. Varför kan man inte använda sig av induktionsbevis här?

Om du försöker använda induktion här, vad händer då?
Uppgiften har gett dig en ledning. Ett ord i uppgiftstexten är kursiverat.
Såhär får jag när jag försöker göra det med induktionsbevis 
det ord i texten som är kursiverat är reella tal.
Varför tror du att de har kursiverat "reella tal"?
När de säger alla reella tal och sen m > 2, är inte 1 och 0 också ett reellt tal?
Alla reella tal, visst innehåller de också decimaltal?
OK, n = p+1, sen då?
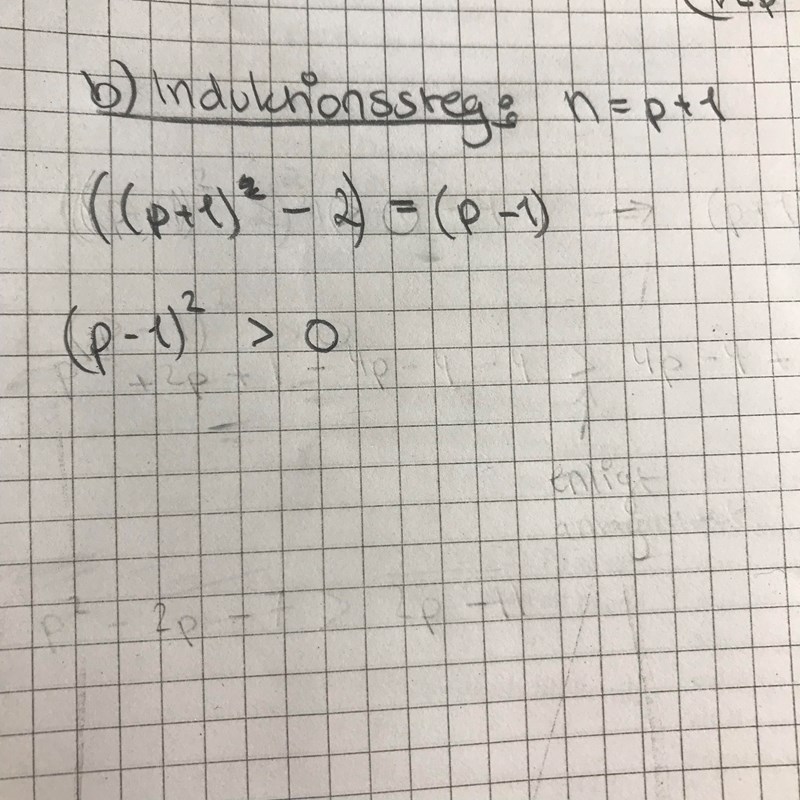 Var inte riktigt säker på hur jag skulle fortsätta
Var inte riktigt säker på hur jag skulle fortsätta
Man behöver inte försöka sig på ett induktionsbevis, allt man behöver konstatera att man enbart kan bevisa ett påstående gällande naturliga tal med induktion. De reella talen är inte del av de naturliga talen, alltså kan man inte utföra något induktionsbevis.
AlvinB skrev:Man behöver inte försöka sig på ett induktionsbevis, allt man behöver konstatera att man enbart kan bevisa ett påstående gällande naturliga tal med induktion. De reella talen är inte del av de naturliga talen, alltså kan man inte utföra något induktionsbevis.
Ja, jag misstänkte det ett tag, för det här är ju diskret matematik och då håller man bara på med heltal.
EDIT: Tack för hjälpen.
Att det inte går beror på att induktionssteget går från ett tal p till nästa tal p+1, och med reella tal finns inget sätt att gå till nästa reella tal och få med alla.





