Variabelsubstitution
Hej!
jag förstår inte hur jag ska lösa nummer 5...
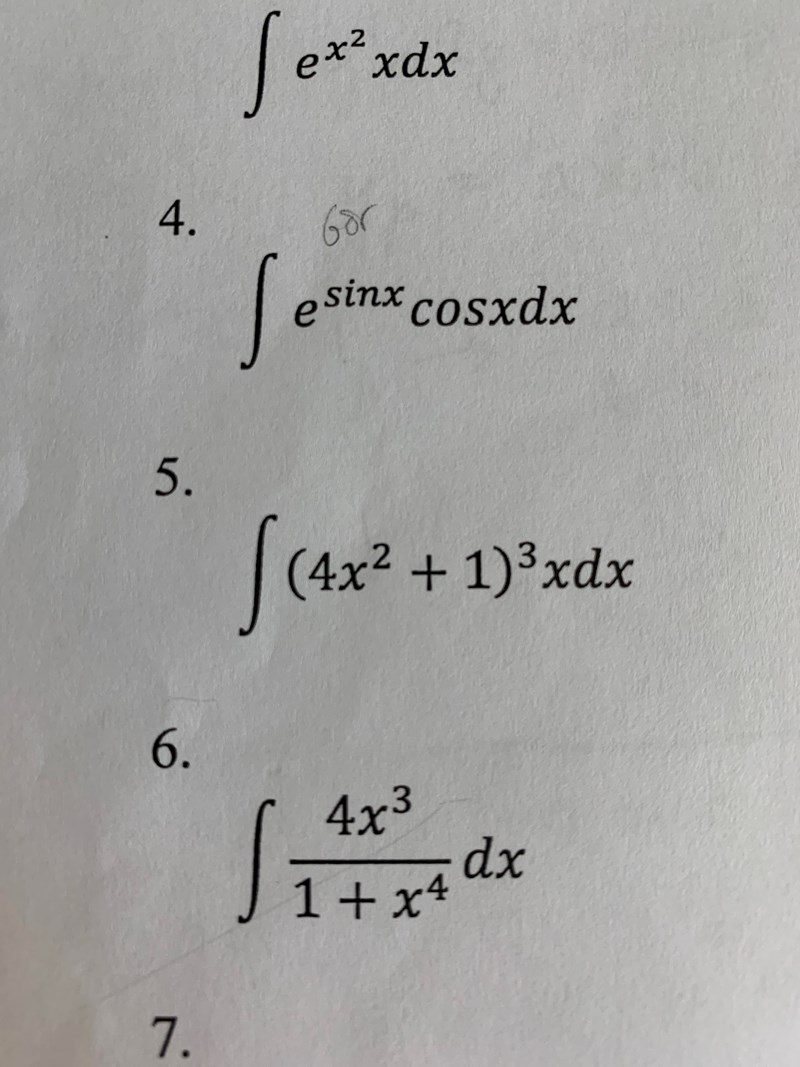
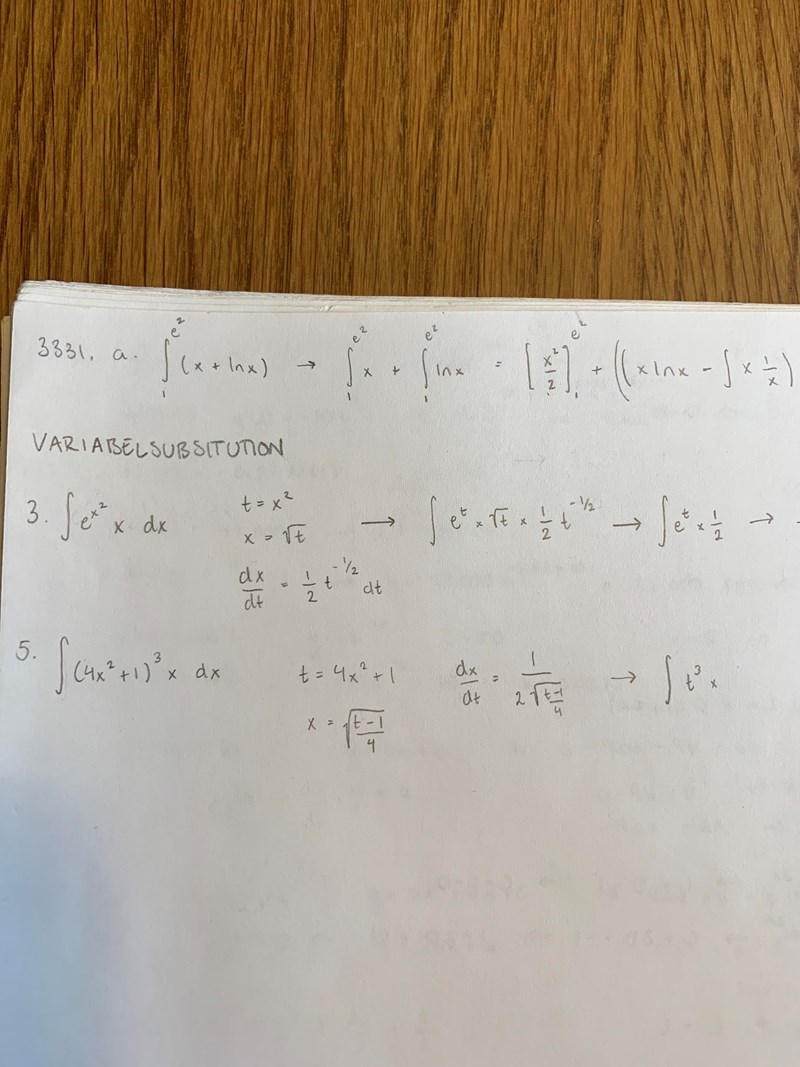
Du har glömt inre derivatan när du räknat dx/dt. Kanske blir det enklare att göra det omvända: räkna ut dt/dx. Kan du sedan lösa ut dt? Det borde gå att byta ut xdx i den ordinarie integralen mot dt*någon konstant
Aa juste det glömde jag...
hur menar du med att räkna ut det omvända? Skulle du kunna visa?
Nu kom jag på vad du menar, ska prova!
När jag istället tar dt/dx får jag 8x och det kan jag ju inte lägga in någonstans i funktionen för att ersätta dx?
Borde gå ganska smidigt. Kolla på den nya integralen där du har fått att dt = 8x dx. Vad händer om du delar båda led med 8?
då får jag ju dt/8 och det jan jag väl inte lägga in i funktionen?
Jo det kan du faktiskt, det är ofta så man vill göra det.
Här ser man att du kan byta ut x dx i den ursprungliga integralen mot dt/8. Detta ger den nya integralen
som är ganska lätt att lösa
Tack! Det hade jag ingen aning om haha
Nu kunde jag lösa den :)
Skönt att det löste sig. Man kan notera att det hade blivit exakt samma svar om du, som du gjorde från början, räknat dx/dt. Med en inre derivata på 1/4 hade du fått . Men eftersom den där kvadratroten egentligen är x kunde du skriva vilket hade gett

