Variabelsubstitution, kubisk cosinus

Det du gjort är att visa något som gäller för periodiska funktioner när man integrerar över dess period. 

(Edit: Funktionen måste nog vara ojämn över perioden.)

Det är väl säkert ett teorem eller en definition du kan hitta någonstans i någon bok men allmänt bör gälla att du kan dela upp integralen först $0\rightarrow \pi$ och sedan $\pi\rightarrow 2\pi$.

Sedan tar du andra integralen och utför substitutionen $t = u-\pi$. Då kommer du få att ursprungliga integralen är lika med noll. 

Tillägg 1

Helt enkelt för att $\cos(t+\pi) = -\cos(t)$.

Tillägg 2

Notera särskilt att man inte kan göra så som du gjorde ser jag nu. Jag tittade inte tillräckligt noggrant på vad du gjorde. Hade det fungerat hade varje periodisk funktion blivit noll över sin period men så är inte fallet. Jämför med om du har integranden $\cos^2(u)$ som inte ska bli noll, så ser du.

På något vis dividerar du med noll genom substitutionen och får ett orimligt svar (förmodligen för att $\sin(2\pi)=\sin(0)=0$).

Okej, det här går lite djupare än jag först uppfattade det. Finns en anledning till att jag inte är matematiker, jag har glömt många subtila saker. Jag ska göra mitt bästa men det finns säkert något sätt att förklara detta på ett enklare sätt.

Principalgren

Problem med denna typ av substitution brukar lösas med något som kallas principalgren, eng: principal branch (Wikilänk).

Exempel

Vi tittar på en liknande integral som för att göra det intressant inte är lika med noll:

$\displaystyle \int_0^{2\pi} \cos^2\left(u\right) \ du$

När vi ansätter substitutionen:

$a = \cos(u)$

Då är det viktigt att vi inser att vi egentligen måste hålla tungan rätt i mun med definitionsmängd och värdemängd. Ovan är nämligen synonymt med att:

$u = \arccos(a)$

Men vi kan inte utan vidare beskriva detta som en funktion $u=u(a)$ därför att samma $a$ kommer ge olika $u$ om vi låter $u\in[0,2\pi]\rightarrow a\in [1,1]$.

Hur definierar vi en funktion?

Som bekant är det enligt Dirichlet ett krav att:

"En variabel y är en funktion av en variabel x, om till varje värde, som x får anta, är ordnat endast ett av de värden som y får anta."

Se grafen för principalgrenen $u\in [0,\pi]$ hos $u(a)=\arccos(a)$ nedan:

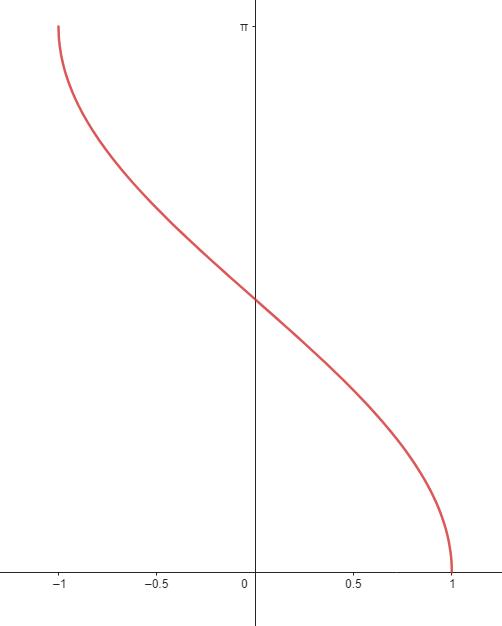
Här har vi inga problem att definiera funktionen $u(a)$ och låta $a\in [-1,1]$ men om vi skulle lägga till grenen $u\in [\pi, 2\pi]$ och alltså låta $a\in[1,1]$ har vi:

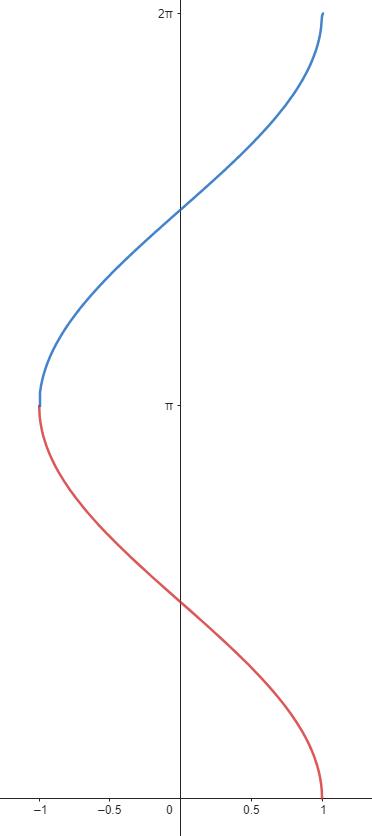
Här ser vi att den blå kurvan har annat värde än den röda för ett givet värde på $a$. Det går därmed inte att definiera en funktion $u(a)$ som låter $a$ löpa hela vägen enligt $a\in[1,1]$.

Slutsats

Funktionen $u(a)$ har alltså nödvändigtvis en begränsad värdemängd vilket innebär att ursprungliga funktionen innan invertering måste ha begränsad definitionsmängd. Vi kan inte gå över hela $0 \rightarrow 2\pi$ utan måste begränsa oss till $0\rightarrow \pi$.

Lösning genom omskrivning

Vi gör ändringen på vår ursprungliga integral enligt:

$\displaystyle \int_0^{2\pi} \cos^2\left(u\right) \ du =\int_{0}^{\pi} \cos^2\left(u\right) \ du+\int_{\pi}^{2\pi} \cos^2\left(u\right) \ du$

Sedan vet vi att $\displaystyle\int_{\pi}^{2\pi} \cos^2\left(u\right) \ du=\int_{0}^{\pi} \cos^2\left(u\right) \ du$ från substitutionen som jag beskrev i förra inlägget. Till slut får vi alltså:

$\displaystyle \int_0^{2\pi} \cos^2\left(u\right) \ du=2\int_{0}^{\pi} \cos^2\left(u\right) \ du$

Arbete med substitutionen

Substitutionen $a=\cos(u)$ ger:

$u=0\rightarrow a=1 \ ; \ u=\pi \rightarrow a=-1$

För att enklast ta fram uttryck för differentialen inverterar vi substitutionen:

$u = \arccos(a)$

$du=-\dfrac{1}{\sqrt{1-a^2}} da$

Detta ger:

$\displaystyle 2\int_{1}^{-1} (-\dfrac{a^2}{\sqrt{1-a^2}})  \ da =\pi$

Ironiskt nog är detta en svårare integral än den vi började med. Som ju egentligen är ganska enkel med användning av formeln för cosinus av dubbla vinkeln.

Vad vi får i ditt fall

I ditt fall blir det ganska enkelt:

$\displaystyle \int_0^{2\pi} \cos^3\left(u\right) \ du =\int_0^{\pi} \cos^3\left(u\right) \ du+\int_{\pi}^{2\pi} \cos^3\left(u\right) \ du=$

Som jag beskrev i mitt förra inlägg skiftar vi nu den andra integralen med $\pi$ vilket ger:

$\displaystyle \int_0^{\pi} \cos^3\left(u\right) \ du+\int_0^{\pi} (-\cos\left(u\right))^3 \ du=0$

För att göra det mer intressant, pröva att räkna ut denna integral istället:

$\displaystyle \int_0^{\pi/2} \cos^3\left(u\right) \ du$

Nu gör ni ett nybörjarproblem jättesvårt..

Tänk bara på variabelbyte som kedjeregeln baklänges. Om vi deriverar F(g(x)) får vi f(g)*g'. Så det man vill göra i variabelbytet är att identifiera g och g' så vi får en in integral som bara är f(g)dg. Cos^2 kan bli sin mha trigg1, så vi kan sätta sin=g och då blir g'dx=cosdx=dg.

Så integrera bara (1-g^2)dg och byt g mot sin i svaret.

Micimacko skrev:

Nu gör ni ett nybörjarproblem jättesvårt..

Ja, uppgiften är enkel med rätt substitution. Jag uppfattade huvudsakliga frågeställningen som:

"... jag undrar om detta är en lyckosam tillfällighet eller om detta resonemang stämmer."

Alltså, att personen inte bara ville ha ett recept på hur den ska göra istället utan lära sig något om varför det den själv hittade på fungerar eller inte fungerar.

SaintVenant skrev:

Micimacko skrev:

Nu gör ni ett nybörjarproblem jättesvårt..

Ja, uppgiften är enkel med rätt substitution. Jag uppfattade huvudsakliga frågeställningen som:

"... jag undrar om detta är en lyckosam tillfällighet eller om detta resonemang stämmer."

Alltså, att personen inte bara ville ha ett recept på hur den ska göra istället utan lära sig något om varför det den själv hittade på fungerar eller inte fungerar.

Det stämmer, är mycket tacksam för ditt utförliga svar tidigare!