Varians och standardavvikelse 2, grundläggande matematisk statistik

Uppgiften är löst på två olika sätt. Den är så grundläggande så texten behövs ej och jag behöver hjälp för att få rätt på det första lösningsförslaget till att bli rätt (ovan streckade linjen). Jag försöker använda följande formel som finns på formelsamlingen:
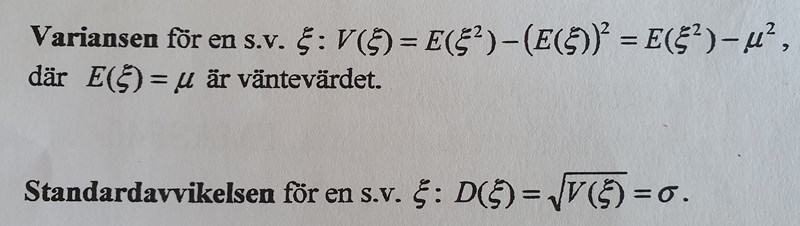
och får fel svar medan jag får rätt svar av att använda formeln som finns i boken (under streckade linjen). Varför får jag fel på den översta?
/🐎
Grundläggande eller inte, jag tror att det är fler än jag som inte anser det är värt mödan att försöka förstå en lösning om man inte vet exakt hur uppgiften är formulerad.
Återkommer imorgon!
"För maskiner som kommer att fungera efter 6 månader har beräknats ha ett väntevärde µ = 1,5 och fördelningen
x 0 1 2 3
P(ξ = x) 0,125 0,375 0,375 0,125
Beräkna varians och standardavvikelse till ξ."
Variant 1:
E(ξ) = 0.125*0 + 0.375*1 + 0.375*2 + 0.125*3= 1.5
E(ξ^2) = 0.125*0^2 + 0.375*1^2 + 0.375*2^2 + 0.125*3^2 = 3
V(ξ) = E(ξ^2) - E(ξ)^2 = 0.75
Variant 2:
V(ξ) = E([ξ - E(ξ)]^2) = 0.125*(0 - 1.5)^2 + 0.375*(1 - 1.5)^2+ 0.375*(2 - 1.5)^2 + 0.125*(3 - 1.5)^2 = 0.75
Tack, nu får jag ihop det och lite till!




