Vart är sin v < cos v

Kanske kan det bli klarare om man ritar funktionernas grafer?

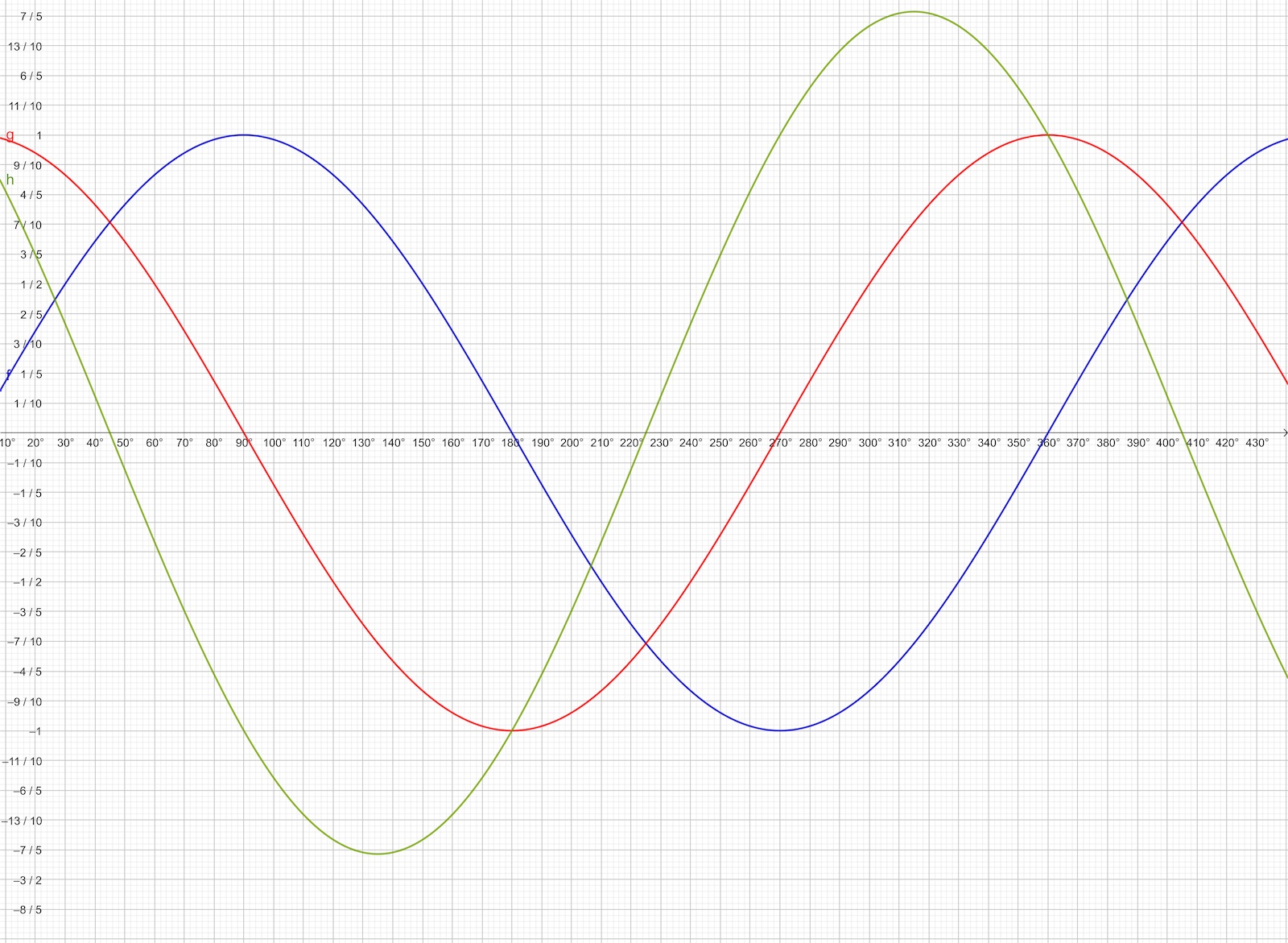
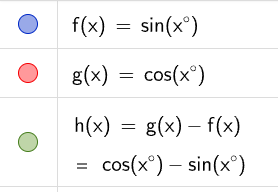
Tyckte tyvärr inte att det blev tydligare... 😅

ok.

Håller du med att för en enhetscirkel gäller

$x = \cos{\alpha}$ och

$y = \sin{\alpha}$?

Jajamän!

Då kan $\cos{\alpha} > \sin{\alpha}$  skrivas som

$x > y$ eller $y < x$.

Det sista kan jämföras med funktionen $y=x$ och då är det punkter under linjen som satisfierar villkoret.

Precis.

Då passande vinklar mellan 0 och 360 är

$0^o<\alpha<45^o$ och

$225^o < \alpha < 360^o$

Det hänger jag med på. Min lärare byggde dock detta svar på 2 resonemang som jag inte förstod hur de kan vara rätt. Jag ser exempelvis inte i grafen hur x kan vara större än y i det markerade området i kvadrant 1. Är inte x=y i det området? 

Man resonera så här:

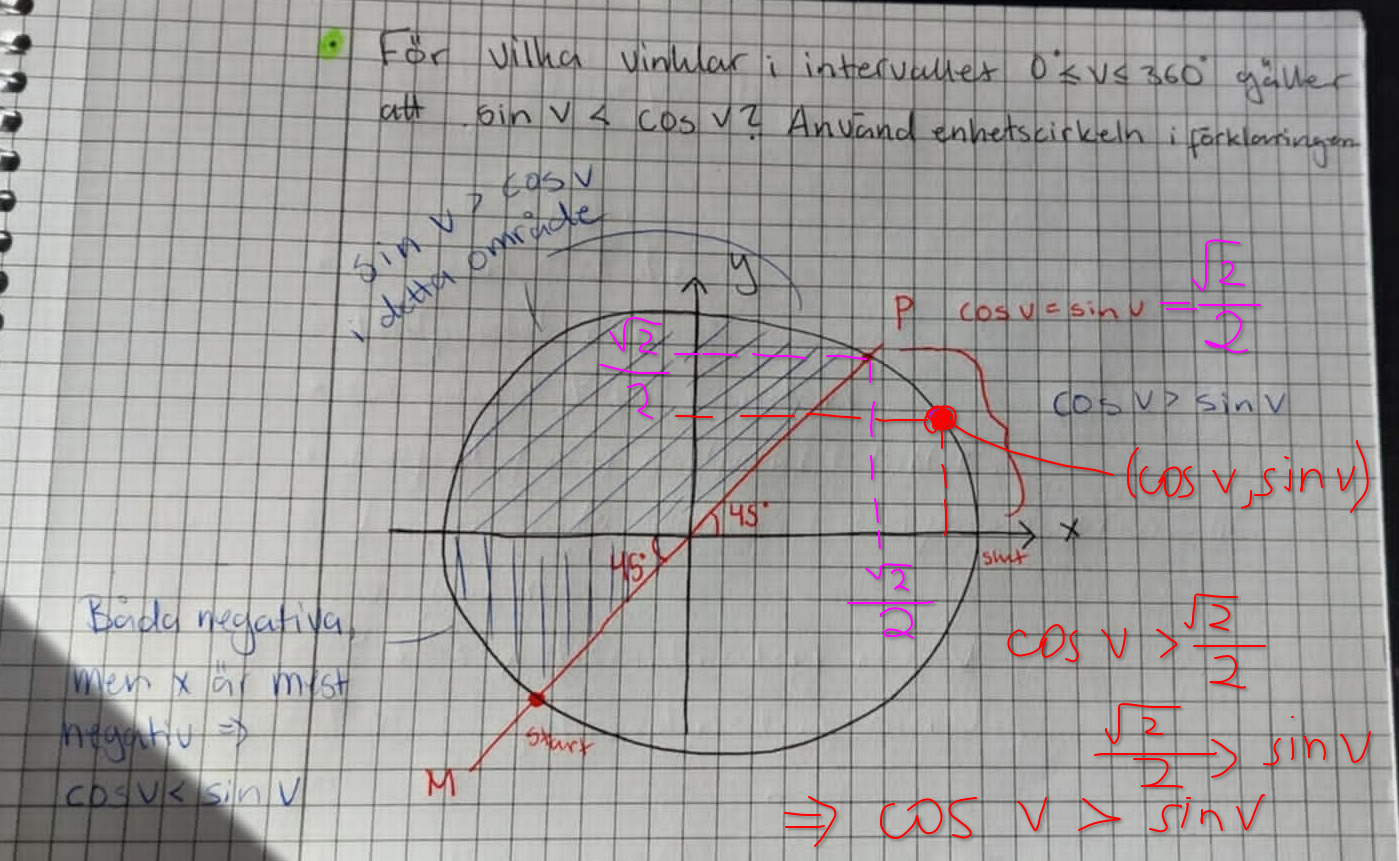
Nu ser jag det! :D Om vi avslutar med min andra fråga undrar jag varför x är mest negativ (x och y är båda negativa) i det markerade områden i tredje kvadranten? När vi passerar 225 grader blir det istället cos v > sin v, varför är y större i det området? 

Med samma bild:

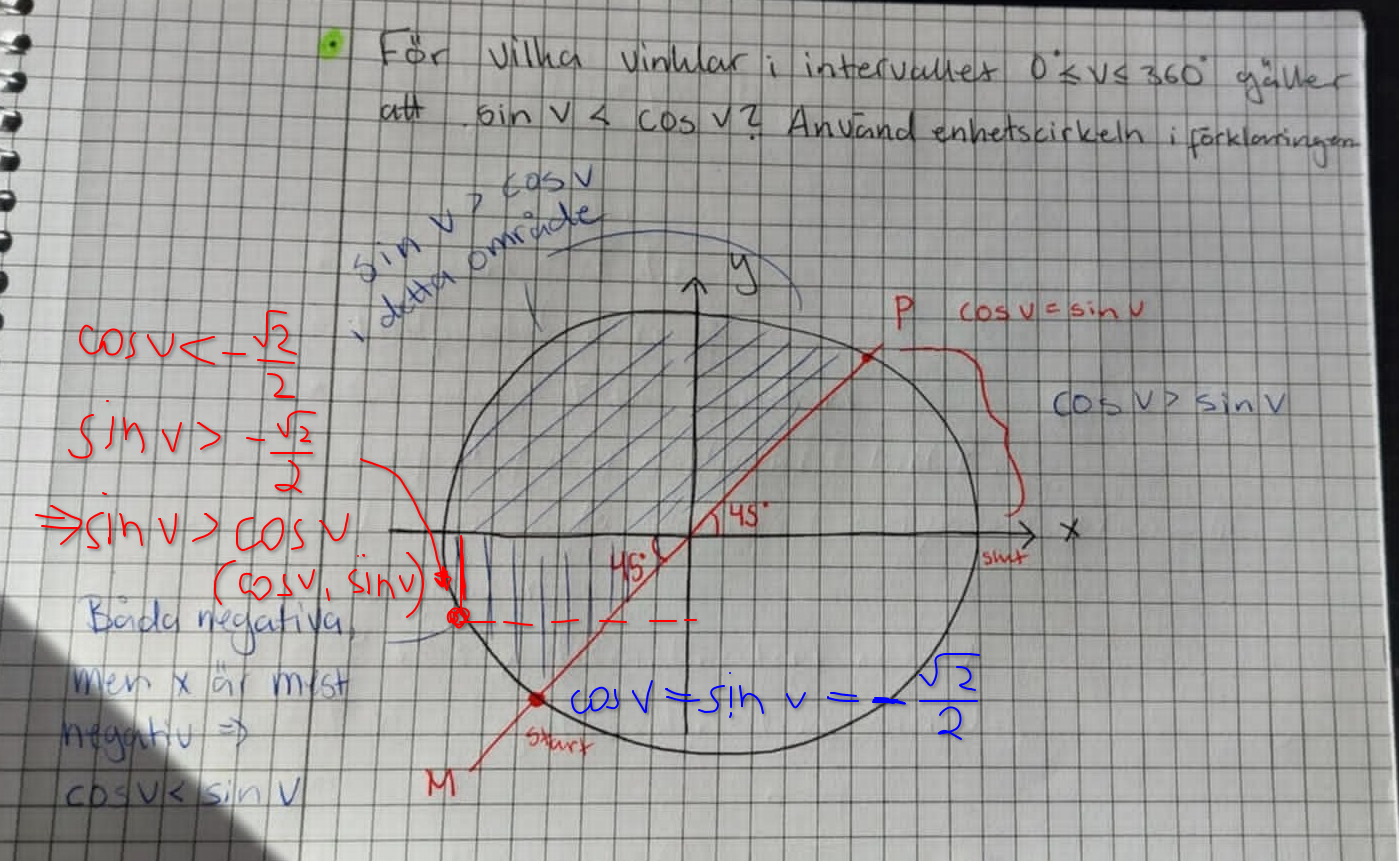
Testa att rita en punkt för en vinkel större än 225⁰ så kommer du fram till att cos v > sin v.

Tack för hjälpen! :)