Växelström

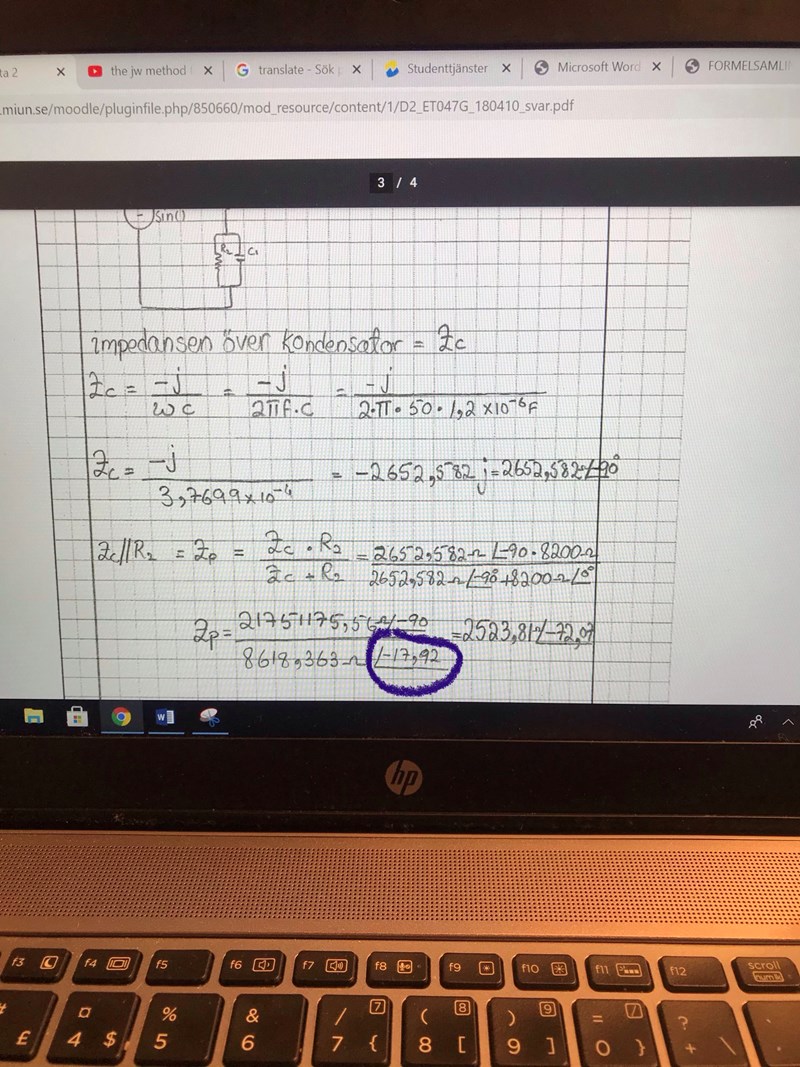
Utveckla detta $2652,582\angle -90\hspace{0.17em}=\hspace{0.17em}a+bi$, sedan addera realdelarna för sig samt imaginärdelarna för sig då du har 8200 helt resistivt och omvandla tillbaka i formen $\left|Z\right|\angle \phi$

Jag vet inte hur jag ska göra det

Ett i min mening mer pedagogiskt sätt att göra det på än att använda sig av ingenjörsnotation är:

$Z_{p} = \dfrac{A e^{j\left(\omega t - 90^{\circ}\right)}}{B e^{j\left(\omega t -17.92^{\circ} \right)}} = \dfrac{A}{B} e^{j\left(\omega t -90^{\circ} - \left(\omega t - 17.92^{\circ} \right) \right)} = \dfrac{A}{B} e^{j \left(-72.08^{\circ} \right)}$

Här är $A=21751175.56$ och $B=8618.363$.

Det jag vill veta är hur han fick -17,92 grader ? 

iqish skrev:

Det jag vill veta är hur han fick -17,92 grader ? 

Du har att:

$R_{2} +Z_{C}= 8200 - 2652.582j$

Skriv nu om detta på exponentiell form:

$\sqrt{8200^{2} + 2652.582^{2}} e^{j\left( \tan^{-1}\left(\dfrac{-2652.582}{8200} \right) \right)}$

Då $\tan^{-1}$-funktionen inte vet om det är nämnare eller täljare som är negativ brukar det vara en bra idé att rita in det komplexa talet i ett komplext talplan för att utröna vad vinkeln är. I detta fall ser du enkelt att:

$\tan^{-1}\left(\dfrac{-2652.582}{8200} \right) \approx -17.92^{\circ}$

Jaha ok 

Så hur blir om jag hade så här istället då? 

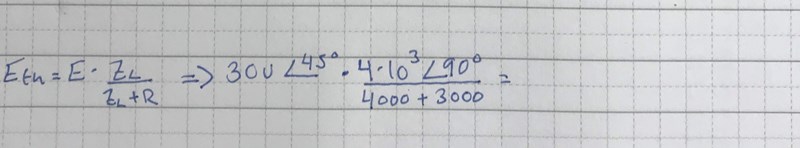Bli det då roten ur (4000^2+3000^2) 

tan^-1=4000/3000 ? 

Tänker jag rätt här ? 

Vill du lära dig genvägen med ingenjörsnotation eller vill du förstå matematiken bakom?

Båda skulle jag säga 

Försökte lösa uppgiften och fick det här svaret la det stämma ?