Vektor A-uppgift
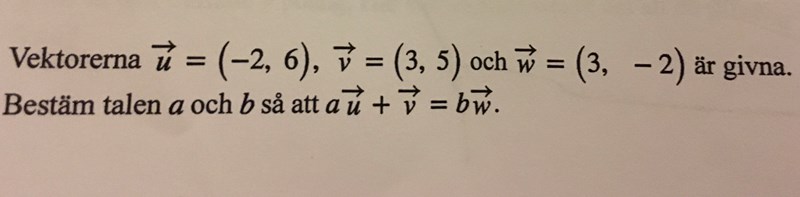 Har försökt att rita upp ett koordinatsystem med vektorerna men kommer inte fram till något. Enligt facit kan man lösa uppgiften geometriskt eller algebraiskt.
Har försökt att rita upp ett koordinatsystem med vektorerna men kommer inte fram till något. Enligt facit kan man lösa uppgiften geometriskt eller algebraiskt.
Tack på förhand
Algebraiskt:
Om så är .
Du behöver även veta hur man adderar vektorer komponentvis och att identiska vektorer har identiska komponenter.
Kommer du vidare då?
Yngve skrev:Algebraiskt:
Om så är .
Du behöver även veta hur man adderar vektorer komponentvis och att identiska vektorer har identiska komponenter.
Kommer du vidare då?
Är inte säker om jag skulle kunna börja så här (efter din ledtråd):
Nästan. Du glömde att multiplicera med b i högerledet.
Yngve skrev:Nästan. Du glömde att multiplicera med b i högerledet.
Aha okej var osäker om det men tack :)
Grejen är att jag inte vet vad jag ska göra här:
(-2a,6a) + (3,5) = (3b,-2b)
Ska jag addera x koordinat för x-koordinat/y för y eller ska jag flytta något?
Ja du ska addera x-koordinaterna för sig och y-koordinaterna för sig.
Räkneregler för vektorer hittar du här.
Scrolla ner till avsnittet om vektorer i koordinatform.
Yngve skrev:Ja du ska addera x-koordinaterna för sig och y-koordinaterna för sig.
Räkneregler för vektorer hittar du här.
Scrolla ner till avsnittet om vektorer i koordinatform.
(-2a+3,6a+5) = (3b,-2b)
Efter det här? Vet ej om man kan ta x/y-delen av ekvationen t.ex -2a+3=3b
mattenörden123 skrev:
(-2a+3,6a+5) = (3b,-2b)
Efter det här? Vet ej om man kan ta x/y-delen av ekvationen t.ex -2a+3=3b
Bra!
Jo det är precus så du ska göra.
Yngve skrev:mattenörden123 skrev:(-2a+3,6a+5) = (3b,-2b)
Efter det här? Vet ej om man kan ta x/y-delen av ekvationen t.ex -2a+3=3b
Bra!
Jo det är precus så du ska göra.
Okej så detta får jag för a:
a=-2/3b+2/3
Känner mig lite vilse eftersom oavsett vad kommer jag väl alltid ha två variablerna kvar? Hur skulle du göra?
Villkoret för x-koordinaterna är
-2a + 3 = 3b
Villkoret för y-koordinaterns är
6a + 5 = -2b
Dessa två villkor måste gälla samtidigt, dvs samma värden på a och b ska uppfylla båda dessa villkor.
Det ger dig ett ekvationssystem med två ekvationer och två obekanta. Ekvationssystemets lösning ger dig a och b.
Har du stött på sådana tidigare?
(Det råkade bli fel när du löste ut a ur villkoret för x-koordinaten.)
Yngve skrev:Villkoret för x-koordinaterna är
-2a + 3 = 3b
Villkoret för y-koordinaterns är
6a + 5 = -2b
Dessa två villkor måste gälla samtidigt, dvs samma värden på a och b ska uppfylla båda dessa villkor.
Det ger dig ett ekvationssystem med två ekvationer och två obekanta. Ekvationssystemets lösning ger dig a och b.
Har du stött på sådana tidigare?
(Det råkade bli fel när du löste ut a ur villkoret för x-koordinaten.)
Hej igen,
Fick fram både a och b igår m.h.a ekvationssystem:
Sedan är det samma sak för a och får då att a=
Tack så jättemycket :)
Bra. Har du kontrollerat resultatet?
Yngve skrev:Bra. Har du kontrollerat resultatet?



