Vektor analys (2)

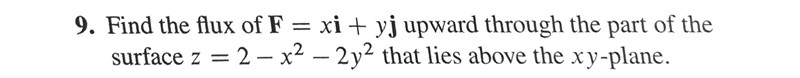
Hej,

• Det verkar som att normalvektorn är fel. Jag får den till $\mathbb{n} = (2u,2v,1)$.
• Du har skrivit en skalärprodukt $F \cdot \mathbb{n}dS$ som är rent nonsens: en vektor i $\mathbb{R}^2$ skalärt med en vektor i $\mathbb{R}^3.$

Du verkar ha missat att $F$ är ett vektorfält i rummet och inte i planet.

Är du säker på att normalvektorn är fel? Min kryssprodukt stämmer ju? Och hur går jag vidare? 

Du har fel yta. z = 2 - x² - 2y², inte z = 2 - x² - y².

Jo, du får fel tecken på ett ställe när du utför kryssprodukten.

Ja! Ser det nu. 

Var står det att x och y skall vara större eller lika med 0? Har du tagit med hela uppgiften?

Ja, det är hela uppgiften. I uppgiften står det: xy-plane.

Då tror jag du tolkar det fel. Det står att vi skall betrakta den delen av ytan som ligger ovanför xy-planet, dvs z > 0, som implicerar att 2 - x² - 2y² > 0, dvs (x/$\sqrt{2}$)² + y² < 1, vilket är området innanför en ellips.

Nej, det blir ändå en svår integral... Facit: $2 \sqrt{2 \pi}$

dvs (x/$\sqrt{2}$)² + y² < 1, vilket är området innanför en ellips.

Hur fick det??

Du har ytan z = 2 - x² - 2y² plus kravet att z > 0, som ger att 2 - x² - 2x² > 0 som går att forma om till den olikheten som jag angav.

Okej förstår! Så jag integrerar över detta område?

Ja. Men om det blir bökigt så titta på vad divF blir för att se om det möjligen kan finnas något bra sätt att använda Gauss sats som kanske ger en enklare väg till målet.

Det här med divF har inte jag försått riktigt! Jag vet hur man räknar ut det, men vad innebär det i dessa sammanhang?

OK glöm det då, det kanske kommer längre fram.

Allmänt gäller att en normal till ytan med parameterframställningen $z=f(x,y)$ är $\mathbf{n}=(-f^{'}_x, -f^{'}_y,1)$

I detta fall är alltså $\mathbf{n}=(2x,4y,1)$, där $\{x,y\}$ ska ligga i det ellipsformade området $D$ i xy-planet. Ytintegralen kan då uttryckas som

$\displaystyle \int_D\,(x,y,0)\cdot (2x,4y,1)\,\mathrm{d}x\mathrm{d}y=\int_D (2x^2+4y^2)\,\mathrm{d}x\mathrm{d}y$

Ellipsen $D$ kan i sin tur ges en parameterframställning genom

$x=\sqrt{2}r\cos(\theta)$

$y=r\sin(\theta)$

$\displaystyle \int_0^{2\pi}\int_0^1 \,(4r^2\cos^2(\theta)+4r^2\sin^2(\theta))\sqrt{2}r\,\mathrm{d}r\mathrm{d}\theta=4\sqrt{2}\int_0^{2\pi} \int_0^{1}\,r^3\,\mathrm{d}r\mathrm{d}\theta$

Tack så mycket PATENTERAMERA och Jroth!